Проектирование горизонтальной и наклонной плоских поверхностей

Задачи вертикальной планировки

Вертикальная планировка — это комплекс работ по преобра­зованию существующего рельефа на стройплощадке для созда­ния нормальных условий эксплуатации объектов, Преобразован­ный рельеф должен обеспечивать упорядоченный сток талых и дождевых вод, удобство для пешеходов, нормальную эксплуата­цию транспорта и т.д.

Данное определение включает основные задачи вертикальной планировки. Можно добавить то,

что она проводится с учетом экономической целесообразности, т.е должен соблюдаться баланс земляных работ, который предусматривает наименьшие объемы перемещения земляных масс и

максимального сохранения естественного рельефа планируемой территории.

Топографическая основа проекта планировки

Для проектирования и расчетов служит топографический план строительной площадки, на который в соответствующем масш­табе наносят сетку квадратов со стороной 5 или 10 м для сложно­го рельефа и 20, 40 или 50 м - для простого. Рядом с вершинами квадратов подписывают отметки: в числителе проектные Н_п , в знаменателе — фактические Н (рис.1). Последние определяют по плану относительно горизонталей существующего рельефа.

Проектные отметки вершин квадратов рассчитывают исходя из ряда условий, в частности необходимость естественного водо­отвода требует проектирования наклонной поверхности искусст­венного рельефа. Если не планируется вывозка или привозка грунтовых масс, то учитывается условие баланса земляных ра­бот, по которому из зоны выемки грунт перемещается в зону насыпи, а объемы выемки равняются объему насыпи.

Проектирование горизонтальной и наклонной плоских поверхностей

Возможны случаи расчетов вертикальной планировки. Рассмотрим три ти­пичные задачи.

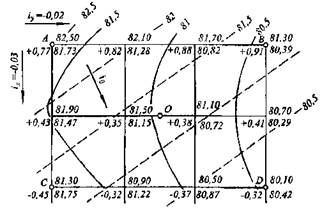
Рис.1. Проектирование наклонной площадки: сплошные линии — горизонтали; штриховые — проектные горизонтали

1. В случае проектирования, горизонтальной площадки при условии баланса земляных работ ее проектная высота Н_п вычис­ляется по формуле

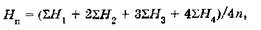(1)

где ΣН₁ — сумма отметок земли у вершин, входящих в один квад­рат; ΣН₂, ΣН₃,ΣН₄ - суммы отметок земли вершин, общих соответственно для 2—4-х квадратов; п — число квадратов.

2. Наклонная плоская площадка задана проектной отметкой Н точки А (см. рис.1) и направлением (дирекционным уг­лом) α₀ наибольшего уклона i_0. Исходя из этого вычисляют зна­чения уклонов i_х по оси х и i_у — по оси у:

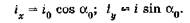(2)

Проектные отметки вершин квадратов вначале последователь­но вычисляются относительно заданной отметки Н_пА, например по линии АВ:

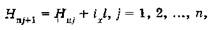(3)

где l — длина стороны квадрата, а затем по перпендикулярным направлениям по этой же формуле, но при уклоне i_у. В нашем при­мере заданы проектная отметка точки А Н_пА = 82,50 и дирекционный угол α₀ = 146° 27' наибольшего уклона i₀= —0,036 (см. рис. 1). Вычисляем уклоны i_х=i₀ соs α₀ = — 0,03; i_у= i₀ sin α₀ = — 0,02. Проверка значений i_х и i_у: = i_х²+i_у² =

= 0,0013= ±0,036. Про­ектные превышения между вершинами квадратов со стороной l = 20 м равны: 1) в направлениях, параллельных оси у: h_у = i_уl = -0,02 • 20 = -0,40 м;

2) в направлениях, параллель­ных оси х: h_х -11 = -0,03 • 20 = -0,60 м. Проектные отметки вершин квадратов, рассчитанные по формуле (3), указаны на рис.1 выше и правее вершин квадратов.

Рабочую отметку h_р (т.е. высоту насыпи или глубину выемки) вычисляют как разность между проектной и фактической (отметка земли) отметками для данной вершины квадрата (в нашем примере на рис.1 значения h_р указаны ниже и левее вершины квадратов).

Объем выемки или объем насыпи грунта в пределах одного квадрата с рабочими отметками h_i одного знака - это объем квад­ратной призмы:

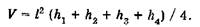(4)

В переходных квадратах, которые пересекает линия нулевых работ (рис. 2), рассчитывают положение этой линии на сторо­нах квадратов по формулам 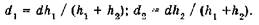(5),

(5)

определяют площади Р_н и Р_в насыпи и выемки и их объемы:

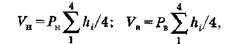(6)

например

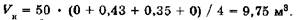
Если сумма объемов грунта по насыпи и выемке не соответствует заданному балансу, то изменяют высоту проектной плоскости и повторяют расчеты.

3. Плоскую наклонную площадку необходимо рассчитывать при условии баланса земляных работ. В этом случае сначала оп­ределяют центр тяжести О проектируемой площадки и его про­ектную отметку Н₀. Относительно центральной точки О вычис­ляют проектные отметки вершин квадратов способом, рассмот­ренным в задаче 2.

Центр тяжести О площадки на рис.1 определяется точкой пересечения диагоналей АD и СВ прямоугольной фигуры АВDС. Положение центров тяжести О₁ и О₂ прямоугольных фигур АРС и РВМК определяют по рис.2. Как известно из механики, центр тяжести О находится на отрезке О₁ О₂ в точке, которая

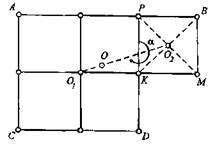
Рис.2. Центр тяжести площадки

делит этот отрезок в отношении λ, обратно пропорциональным площадям Р₁ и Р₂ данных фигур, т.е. λ = Р₂ / Р₁ В нашем приме­ре λ = 1/4, т.е. О₁О = (О₁О₂) / 4. Вычислив отрезок О₁О, найдем положение точки О.

Аналитически координаты х_о, у_о центра тяжести О вычисля­ются по известным координатам х₁, у₁ и х₂, у₂ точек О₁ и О₂ :

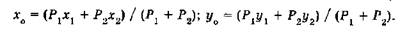
В общем случае, когда площадка характеризуется сложной формой, координаты ее центра тяжести

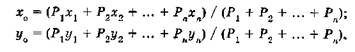
где х_i, у_i — координаты центра тяжести фигуры, площадь кото­рой равна Р_i.

Проектную высоту Н_о центра тяжести О определяют по форму­ле (1), затем находят начальную проектную высоту Н_н одной из вершин квадрата, внутри которого найдена точка О. Для этого по плану измеряют расстояние d = ОО₁ и с помощью транспортира находят дирекционный угол α направления ОО₁. Проектная высо­та начальной точки О₁ равна

Н = Н_о + i_о соs (α —α_о).

Дальнейшие вычисления производятся по формулам (2) и (3) относительно точки О₁ с высотой Н_н.