Гироскопические силы
Исследование законов вращательного движения абсолютно твердого тела на примере гироскопа.
Волчок
Внимание многих ученых и изобретателей привлекла древнейшая народная игрушка - волчок (рис.1), которой придавали самые различные формы (рис.2).
 Рис.1. Волчок
Рис.1. Волчок
Большей частью волчок приводили во вращение с помощью тонкой бечевки, предварительно намотанной на его вал. Быстро сдергивая бечевку с вала волчка, сообщали последнему вращение вокруг оси АА1, которое продолжалось до тех пор, пока силы трения, действующие в точке О опоры волчка о какое-либо основание, не прекращали его движение.
 Рис.2 Различные формы волчков
Рис.2 Различные формы волчков
Попытки повалить быстро вращающийся волчок на бок не удавались. Под действием толчка с силой волчок лишь отскакивал в сторону и продолжал вращаться вокруг вертикальной оси ВВ1, положение которой было лишь несколько смещено относительно первоначального направления АА1.
Удивительное свойство волчка сохранять неизменным направление оси АА1 своего вращения открывало широкие перспективы для его практического использования. В самом деле, если быстро вращающийся волчок, выполненный в виде диска, неизменно выдерживает вертикальное положение, то вращение самого диска будет происходить строго в горизонтальной плоскости.
Возникла непосредственная возможность практического осуществления искусственного горизонта.
Изучением законов движения волчка занялись многие ученые мира. Над этой задачей работал и знаменитый английский ученый И. Ньютон (1642 - 1727) и член Российской академии наук Л. Эйлер (1707 - 1783). Эйлер в 1765 г. впервые опубликовал теорию движения твердого тела около неподвижной точки его опоры и тем самым создал теоретическую базу для дальнейшего более глубокого изучения законов движения волчка. Работы французских ученых Ж. Лагранжа (1736-1813) и Л. Пуансо (1777 - 1859) во многом содействовали дальнейшему изучению и разработке методов практического использования свойств быстро вращающегося волчка.
Представим себе какой-либо волчок, например то, что описан в начале книги, - тонкий латунный диск (шестеренка), насаженный на тонкую стальную ось.
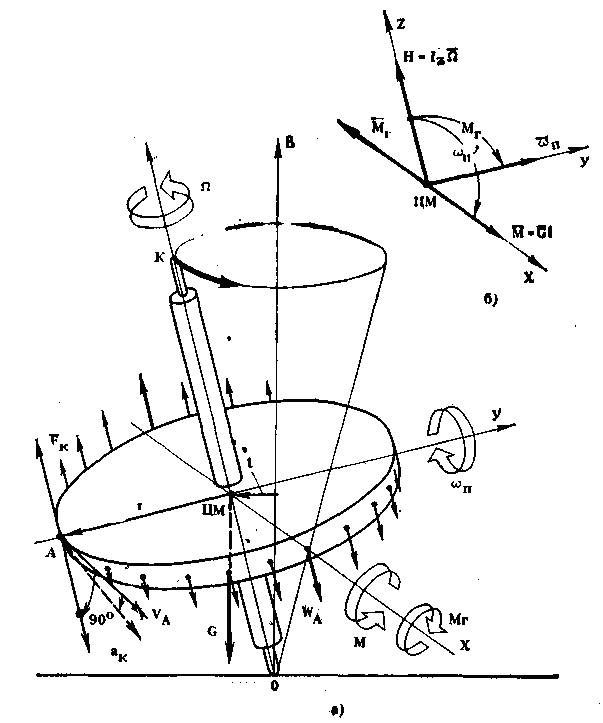
Рис.4. Схема, поясняющая возникновение прецессии, гироскопического момента и характера движении полчка
Возьмем прямоугольную систему координат хуz и поместим ее центр в центр масс волчка, то есть в точку ЦМ. Пусть ось z проходит через ось собственного быстрого вращения волчка, тогда оси хуz будут параллельны плоскости диска и лежать внутри него. Договоримся, что оси хуz участвуют во всех движениях волчка, кроме его собственного быстрого вращения.
В правом верхнем углу (рис.4, б) изобразим такую же систему координат хуz. Она нам понадобится в дальнейшем для разговора на "языке" векторов.
Сначала не будем раскручивать волчок, и попытаемся его поставить нижним концом оси на опорную плоскость, например на поверхность стола. Результат не обманет наших ожиданий: волчок обязательно упадет на бок. Почему это происходит? Центр масс волчка (точка ЦМ) лежит выше точки его опоры (точки О). Сила веса Gволчка, как мы уже знаем, приложена в точке ЦМ. Поэтому любое малое отклонение оси z волчка от вертикали В обусловит появление плеча силы G относительно точки опоры О, то есть появление момента М, который и повалит волчок в направлении своего действия, то есть вокруг оси х.
Теперь раскрутим волчок вокруг оси z до большой угловой скорости Ω. Пусть по-прежнему ось z волчка отклонена от вертикали В на малый угол, т.е. на волчок действует тот же момент М. Что же изменилось теперь? Как мы увидим дальше, изменилось многое, а вот в основе этих изменений лежит тот факт, что теперь каждая материальная точка i диска уже имеет линейную скорость V, обусловленную вращением диска с угловой скоростью Ω.
Выделим одну точку в диске, например точку А, имеющую массу mA и лежащую в средней плоскости диска на расстоянии г от оси вращения (г - радиус диска). Рассмотрим особенности ее движения за один оборот.
Итак, в начальный момент времени точка А, как и все другие точки диска, имеет линейную скорость, вектор которой VА лежит в плоскости диска. На волчок (и его диск) действует момент М, который пытается* опрокинуть волчок, придав точкам диска линейные скорости, векторы которых Wi перпендикулярны плоскости диска.
Под действием момента М точка A начинает приобретать скорость WA. В силу закона инерции скорость материальной точки мгновенно нарасти никак не может. Поэтому в начальном положении (точка А находится на оси у) ее скорость WA=0, и только через четверть оборота диска (когда точка А, вращаясь, будет уже находиться на оси х) ее скорость WA возрастает и станет максимальной. Это значит, что под действием момента М вращающийся волчок поворачивается вокруг оси у, а не вокруг оси х (как это было с нераскрученным волчком). В этом явлении начало разгадки тайны волчка.
Поворот волчка под действием момента М называется прецессией, а угловая скорость поворота - скоростью прецессии, обозначим ее ы п. Прецессируя, волчок начал поворот вокруг оси у.
Это движение является переносным по отношению к собственному (относительному) вращению волчка с большой угловой скоростью Ω.
В результате переносного движении вектор относительной линейной скорости VA материальной точки A, уже возвратившейся и начальное положение, окажется повернутым в сторону переносного вращении.
Таким образом, возникает уже знакомая нам картина влияния переносного движения на относительное, влияния, рождающего Кориолисово ускорение.
Направление вектора Кориолисова ускорения точки А, найдем, повернув вектор относительной скорости VА точки А на 90° в сторону переносного (прецессионного) вращения волчка. Кориолисово ускорение ак точки A, имеющей массу тА, порождает силу инерции FK, которая направлена противоположно вектору ускорения aк и приложена к материальным точкам диска, соприкасающимся с точкой A.
Рассуждая подобным образом, можно получить направления векторов Кориолисова ускорения и силы инерции для любой другой материальной точки диска.
Вернемся к точке А. Сила инерции FK на плече r создает момент МГА, действующий на волчок вокруг оси х. Этот момент, порожденный Кориолисовой силой инерции, называется гироскопическим.
Его величину определяют помощью формулы:
МГА = rFk = mAr2 ΩωП = IA Ω ωП
Величину IA = mAr2, зависящую от массы точки и ее расстояния от оси вращения, называют осевым моментом инерции точки. Момент инерции точки является мерой ее инертности во вращательном движении. Понятие момента инерции было введено в механику Л. Эйлером.
Моментами инерции обладают не только отдельные точки, но и целые тела, поскольку они состоят из отдельных материальных точек. Имея это в виду, составим формулу для гироскопического момента МГ, создаваемого диском волчка. Для этого в предыдущей формуле заменим момент инерции точки IA на момент инерции диска IД, а угловые скорости Ω и ωП оставим прежними, так как все точки диска (за исключением тех, что лежат соответственно на осях гну) вращаются с одинаковыми угловыми скоростями Ω и ωП.
Н.Е. Жуковский "отец русской авиации", занимавшийся также и лучением механики волчков и гироскопов, сформулировал следующее простое правило для определения направления гироскопического момента (рис.4, б): гироскопический момент стремится совместить вектор кинетического момента Н с вектором угловой скорости переносного вращения ωП по кратчайшему пути.
В частном случае скоростью переносного вращения является скорость прецессии.
На практике пользуются также аналогичным правилом для определения направления прецессии: прецессия стремится совместить вектор кинетического момента Н с вектором момента физических сил М по кратчайшему пути.
Эти простые правила лежат в основе гироскопических явлений, и мы ими будем широко пользоваться в дальнейшем.
Но вернемся к волчку. Почему он не падает, поворачиваясь вокруг оси х, ясно - препятствует гироскопический момент. Но может быть, он упадет, поворачиваясь вокруг оси у в результате прецессии? Тоже нет! Дело в том, что, прецессируя, волчок начинает поворачиваться вокруг оси у, а это значит, что сила веса G начинает создавать момент, действующий на волчок вокруг этой же оси. Такая картина нам уже знакома, с нее мы начинали рассмотрение поведения вращающегося волчка. Стало быть, и в этом случае возникнут процессия и гироскопический момент, которые не позволят волчку долго наклоняться вокруг оси у, а переведут движение волчка в другую плоскость, и которой нее явлении повторятся снова.
Таким образом, пока угловая скорость собственного вращения волчка Ω велика, момент силы тяжести вызывает прецессию и гироскопический момент, которые удерживают волчок от падении в каком либо одном направлении. Этим объясняется устойчивость оси r вращения волчка. Допуская некоторые упрощения, можно считать, что конец оси волчка, точка К движется по окружности а сама ось вращения z описывает в пространстве конические поверхности с вершинами в точке О.
Вращающийся волчок представляет собой пример движения тела, имеющего одну неподвижную точку (у волчка это точка О). Задача о характере движения такого тела сыграла важную роль в развитии науки и техники, ее решению посвятили свои труды многие выдающиеся ученые.
Рождение гироскопа
Гироскоп — устройство, способное реагировать на изменение углов ориентации связанного с ним тела относительно инерциальной системы координат.
Основано на законе сохранения вращательного момента (момента импульса). Термин впервые введен Жаном (Бернаром Леоном) Фуко в 1852 году.
Получив медицинское образование, Жан Бернар Леон Фуко (1819 - 4868) увлекся экспериментальной физикой и достиг в этой области немалых успехов. Назовем лишь самые крупные - токи Фуко, маятник Фуко, гироскопы.
Слово "гироскоп", придуманное Л. Фуко, состоит из двух греческих слов: "гирос" - вращение и "скопео" - наблюдать, смотреть.
Итак, гироскоп - это "наблюдатель вращения". Сейчас гироскопы "наблюдают" вращение самых разнообразных объектов - кораблей, самолетов, ракет, спутников и многих других. Л. Фуко, создавая свой лабораторный прибор (гироскоп), хотел с его помощью наблюдать вращение Земли относительно абсолютного пространства.
Идея прибора основывалась на теоретическом положении Л. Эйлера о том, что быстровращающееся тело, имеющее одну неподвижную точку и не подверженное действию моментов внешних сил, сохраняет неизменным положение оси своего вращения в абсолютном пространстве. Л. Фуко рассуждал примерно так. Поскольку Земля вращается в абсолютном пространстве, то должно наблюдаться движение предметов, расположенных на ее поверхности, по отношению к оси такого быстровращающегося тела.
Приступая к созданию своего прибора, Л. Фуко сразу же столкнулся с тремя взаимосвязанными проблемами, ставшими потом классическими в гироскопической технике:
1) как практически реализовать тело, имеющее одну неподвижную точку и, стало быть, свободу вращения вокруг трех взаимно перпендикулярных осей;
2) как раскрутить это тело вокруг одной из его осей и в дальнейшем поддерживать высокое значение угловой скорости;
3) как "защитить" вращающееся тело от действия внешних возмущающих моментов,
В качестве тела, предназначенного для быстрого вращения, Л. Фуко выбрал маховик, который был установлен в кардановом подвесе.
Прежде чем объяснить, как устроен карданов подвес, широко применяющийся в технике и в наше время, стоит сказать несколько слов о человеке, чье имя он носит.
Джероламо Кардано (1501 - 1576) - итальянский философ, врач, математик и техник - легендарная личность. Хилый от рождения, он был могуч духом, очень хотел прославиться.
Обладал выдающимися способностями и редким трудолюбцем; жил активно - участвовал в научных диспутах, рьяно занимался медициной и физкультурой, азартно играл в шахматы и кости, много писал, работал с наслаждением.
В своей книге "О моей жизни..." Д. Кардано, подводя итог сделанному, написал: "Число разрешенных мною проблем и вопросов доходит до 40 тысяч; и более мелких указаний я оставляю после себя до 200 тысяч. Вот основания, почему светоч нашей отчизны (Андреа Альчиати - видный юрист начала XVI в. - Ред) назвал меня "мужем открытий".
Однако этот "муж открытий" был не очень щепетилен в вопросах приоритета, и многие истины, известные и до него (сознательно или искренне заблуждаясь, теперь не установить), публиковал под своим именем. В частности, это относится и к карданову подвесу, который еще в XIII в. был описан французским архитектором Уйларсом де Гонкуром.
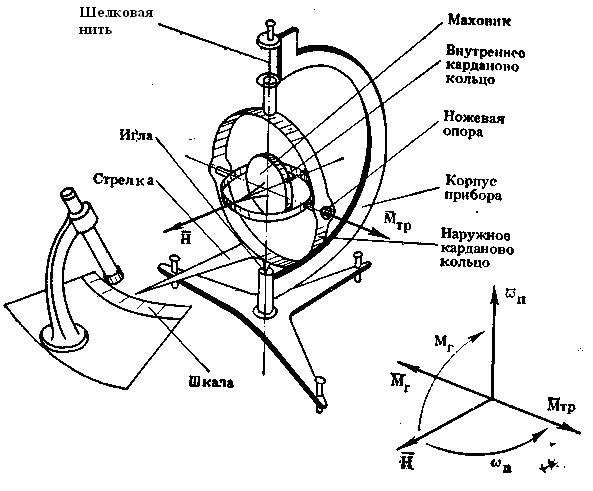
Рис.5. Схема модели первого гироскопа Л. Фуко, 1852 г.
В настоящее время разработано много кинематических схем карданова подвеса, широко применяемых в гироскопической технике. Однако мы вернемся к тому варианту, который применил в своем приборе.Д. Фуко (рис.5). Ось вращения маховика на подшипниках была установлена в кольце, полуоси которого были выполнены в виде трехгранных призм ("ножей"). Ось вращения ножевых опор составляла прямой угол с осью вращения маховика. Стальные полированные "подушки", №а которые опирались грани ножей, были установлены в другом кольце. Это кольцо сверху с помощью шелковой нити подвешивалось к корпусу прибора, а снизу упиралось в корпус иглой. Для наблюдения за движением оси вращения маховика относительно поверхности Земли на кольце была укреплена длинная стрелка (поверхность Земли в данном приборе представляла подставка прибора со шкалой). Кольца называются соответственно внутренним и наружным кардановыми кольцами. Эти два кольца вместе с установленными на них опорами образуют механическую систему, называемую кардановым подвесом. Карданов поднес позволяет установленному в нем телу одновременно поворачиваться вокруг трех взаимно перпендикулярных осей (обеспечивает телу три вращательные степени свободы). Так, например, маховик, установленный в приборе Л. Фуко, мог вращаться вокруг собственной оси (первая степень свободы), вместе с внутренним кольцом карданова подвеса мог поворачиваться вокруг осп ножевых опор (вторая степень свободы) и вместе с внутренним и наружным кольцами карданова подвеса мог поворачиваться вокруг вертикальной оси, слегка закручивая шелковую нить (третья степень свободы).
В своем приборе Л. Фуко постарался в максимальной степени выполнить условия Эйлера: вращающееся тело (маховик) имело одну неподвижную точку, а именно точку пересечения осей маховика, внутреннего и наружного кардановых колец; чтобы свести к минимуму возмущающие моменты, действующие на маховик, были применены самые совершенные из известных тогда опор - ножевые опоры и шелковая нить; узел "маховик - внутреннее кольцо" был тщательно отбалансирован, то есть центр масс узла был совмещен с неподвижной точкой, что в отличие от волчка сводило к пулю момент, создаваемый силой тяжести самого узла. Отмечая низкий уровень возмущающих моментов, Л. Фуко писал, что подвижные узлы прибора "приходили в движение от малейшего дуновения".
Почему так много внимания уделил Л. Фуко устранению моментов внешних сил? Что бы произошло, если бы вокруг осей карданова подвеса действовали бы достаточно большие возмущающие моменты, например моменты трения опор?
Предположим, что маховик раскручен и обладает кинетическим моментом Н, а вокруг оси внутреннего кольца карданова подвеса действует момент трения МTP, создаваемый ножевыми опорами.
Действие своего прибора Л. Фуко продемонстрировал членам Парижской академии наук 27 сентября 1852 г.
С помощью специального устройства маховик был приведен н быстрое вращение и дальше работал на выбеге. Ось вращения маховика была выставлена в плоскость горизонта (направлена горизонтально). Стрелка, связанная с наружным кардановым кольцом, установлена на нулевой отметке шкалы.
Ожидалось, что ось маховика начнет совершать кажущийся поворот вокруг вертикальной оси прибора со скоростью, равной вертикальной составляющей скорости вращения Земли на широте Парижа.
Так как ожидался достаточно медленный поворот стрелки, то для наблюдения за ее движением применялся микроскоп. Опыт удался частично: только в первые минуты после запуска маховика стрелка действительно двигалась справа налево, а затем движение ее становилось хаотичным. Объяснялось это тем, что маховик слишком быстро терял скорость вращения и даже незначительные возмущающие моменты трения ножевых опор вызывали хаотическую прецессию оси маховика в плоскости горизонта.
Уже первые опыты обнаружили еще одно интересное свойство гироскопа - практическую безинерционность прецессионного движения маховика. Если к маховику мгновенно приложить и спять момент внешних сил (па-пример, слегка ударить молоточком но внутреннему кольцу карданова подвеса), то также практически мгновенно возникнут и исчезнут угловая скорость прецессии и гироскопический момент (явления, связанные с квазиупругим эффектом, здесь не рассматриваются). В результате внутреннее кольцо не повернется вокруг своей оси. Всякое другое материальное тело в подобной ситуации продолжало бы двигаться по инерции, отклоняясь все дальше от начального положения.
У маховика гироскопа движение по инерции также есть, но оно. выражается не в одностороннем отклонении от начального положения, а в мелком, быстро затухающем дрожании около этого положения.
Мелкое, быстро затухающее дрожание маховика называется нутацией, что в переводе с латинского языка означает "колебание".
В своих докладах Парижской академии наук Д. Фуко указал также на то, что маховик его прибора, лишенный одной степени свободы, должен стремиться совместить ось своего вращения с вектором абсолютной переносной скорости вращения основания. Теперь этот результат легко можно получить с помощью правила И.Е. Жуковского, во времена же Д. Фуко это было неожиданным открытием. Впечатление еще более усилилось, когда Л. Фуко пояснил, что с помощью гироскопа, имеющего только дне степени свободы, можно определять направление па Северный полюс Земли и широту места установки прибора. Представим себе гироскоп, маховик которого имеет только две степени свободы, а именно: вращение с большой скоростью вокруг собственной оси и возможность поворота вокруг оси внутреннего карданова кольца. Позже подобные приборы стали называться гироскопами с двумя степенями свободы, или двухстепенными гироскопами. Л. Фуко рассмотрел два характерных положения двухстепенного гироскопа относительно поверхности вращающейся Земли.
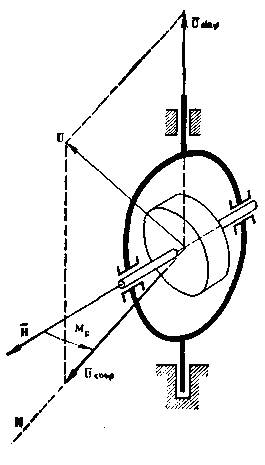
Рис.6. Гирокомпас Л. Фуко
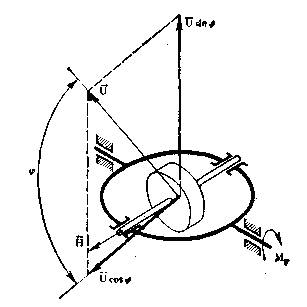
Рис.7. Гироширот Л. Фуко
Мерное: ось внутреннего кольца карданова подвеса вертикальна, и гироскоп участвует в переносном вращении Земли со скоростью U, вектор которой может быть разложен на две составляющие Ūsinφ и Ūcosφ (рис 6). В этом случае в соответствии с правилом Н.Е. Жуковского возникают два гироскопических момента. Один из них будет стремиться совместить вектор Н с вектором Ūsinφ. Но этого совмещения не произойдет, так как на пути совмещения стоят опоры внутреннего кольца карданова подвеса. Этот момент будет создавать лишь давление на опоры.
Другой гироскопический момент будет стремиться совместить вектор Н с вектором Ūcosφ. Это совмещение, возможно, так как опоры допускают поворот маховика вокруг вертикальной оси. Совершая затухающие колебания в горизонтальной плоскости, ось вращения маховика через некоторое время совместится с направлением вектора Ūcosφ. Но ведь вектор Ūcosφ лежит в плоскости меридиана и направлен на Северный полюс Земли! Значит, материальное тело - ось вращения маховика - также будет направлено на Северный полюс Земли. Получился компас, который в отличие от магнитного компаса указывает направление по на магнитный, я на географический полюс Земли.
Этот прибор позднее был нашли гироскопом Фуко первого; рода, или гирокомпасом Фуко.
Второе положение гироскопа: ось внутреннего кольца адрданова подноса горизонтальна, а ось маховика расположена в плоскости меридиана (рис 7). В этом случае также возникнет гироскопический момент, который совместит вектор Н с вектором U. В совмещенном положении угол между осью вращения маховика и горизонтальной плоскостью оказывается равным широте φ. Этот прибор позднее был назван гироскопом Фуко второго рода, или гироширотом.
Таким образом, особым свойством двухстепенного гироскопа является его способность мгновенно реагировать на угловую скорость вращения основания, на котором он установлен, пытаясь совместить по кратчайшему пути ось вращения маховика (вектор кинетического момента) с соответствующей составляющей вектора угловой скорости вращения основания.
Лишив трехстепенной гироскоп одной степени свободы, Л. Фуко открыл замечательное свойство двухстепенного гироскопа.
Ну а если пойти дальше и лишить маховик гироскопа второй степени свободы, не получим ли мы притом каких-либо полезных эффектов? Получим.
Уже давно известно, что вращающийся маховик способен запаса и, кинетическую энергию, которую затем он может расходовать на приведение и действие различных механизмов и па повышение плавности их работы.
В частности, всем знакомы детские игрушки инерционные автомобильчики. Чиркнув пару раз колесами такого автомобиля по полу, раскручивают маховичок, установленный внутри него. А затем уж маховичок, отдавая свою энергию колесам автомобиля, заставляет его двигаться.
Эта идея используется не только в игрушках.
Сегодня разрабатываются транспортные средства с экологически чистыми маховичными двигателями. Уже по улицам городов движутся опытные образцы троллейбусов и автобусов, приводимые в движение энергией маховиков.
Возникают ли гироскопические моменты в маховичных приводах? Конечно, возникают, но так как, кроме собственного вращения, других степеней свободы маховик не имеет, то и его видимого движения не наблюдается.
Гироскопические моменты в этом случае оказывают лишь давление на опоры маховика, что является отрицательным явлением.
Таким образом, хотя маховичные приводы - очень полезные устройства, к гироскопическим приборам они прямого отношения не имеют.
Итак, в своих работах Л. Фуко указал на принципиальную возможность создания гироскопических приборов трех различных назначений: свободного гироскопа, способного хранить неизменной ориентацию оси маховика в абсолютном пространстве, гироскопического компаса, гироскопического измерителя широты
Радиоуправляемые вертолёты, которые оснащены гироскопом, в воздухе намного устойчивее, чем радиоуправляемые вертолеты, которые не имеют в комплектации гироскопа. Они обеспечивают плавный полет, они не сбиваются с намеченного курса при попадании в воздушную яму. Радиоуправляемые вертолеты с гироскопом позволяют новичкам пилотам, очень быстро освоить основные принципы пилотажа и азов полета. Одной из лучших моделей на радиоуправлении с гироскопом является трехканальный радиоуправляемый вертолет с соосной схемой винтов.
Напрямую связано с появлением кориолисовой силы это свойство гироскопа. Так гироскоп при действии момента внешней силы вначале начинает поворачиваться именно в таком направлении действия возникающего внешнего момента, так называемый нутационный бросок. При этом все частицы гироскопа благодаря возникающему моменту будут в это время передвигаться с переносной угловой скоростью его вращения. Однако роторный гироскоп, кроме этого, и сам тоже вращается, следовательно, каждая частица гироскопа будет иметь свою относительную скорость. Поэтому возникает кориолисова сила, которая и будет пытаться заставить гироскоп двигаться только в перпендикулярном направлении, благодаря приложенному моменту, то есть выполнять прецессию. Прецессия будет вызывать кориолисову силу, момент которой скомпенсирует момент внешней силы.
СВОЙСТВА
Основное свойство гироскопа — способность сохранять неизменное направление оси вращения при отсутствии воздействия на неё моментов внешних сил 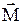 , что следует из закона сохранения момента импульса:
, что следует из закона сохранения момента импульса: 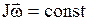 ,если
,если  .. То есть, как бы не поворачивался корпус - ротор всегда будет в одном положении в пространстве.
.. То есть, как бы не поворачивался корпус - ротор всегда будет в одном положении в пространстве.

↑ Сферический гироскоп в вакууме (т.е. общая модель).
При воздействии момента внешней силы вокруг оси, перпендикулярной оси вращения ротора, гироскоп начинает поворачиваться вокруг оси процессии, которая перпендикулярна моменту внешних сил.
Данное свойство напрямую связано с возникновением, так называемой кориолисовой силы (одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения). Так, при воздействии момента внешней силы гироскоп поначалу будет вращаться именно в направлении действия внешнего момента. Каждая частица гироскопа будет таким образом двигаться с переносной угловой скоростью вращения из-за момента. Но роторный гироскоп, помимо этого, и сам вращается, значит, каждая частица будет иметь относительную скорость. Следовательно, возникнет кориолисова сила, которая будет заставлять гироскоп двигаться в перпендикулярном приложенному моменту направлении, то есть процессировать. Прецессия вызовет кориолисову силу, момент которой скомпенсирует момент внешней силы.
Другое свойство гироскопа состоит в том, что при кратковременном воздействии на ось гироскопа она сохраняет свое направление в пространстве. Действительно, из основного закона динамики вращательного движения
следует, что если момент внешних сил  действует в течение короткого времени
действует в течение короткого времени  , то изменение момента импульса гироскопа
, то изменение момента импульса гироскопа 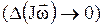 стремится к нулю, и ось гироскопа сохраняет свое направление в пространстве.
стремится к нулю, и ось гироскопа сохраняет свое направление в пространстве.
 Если момент внешних сил, действующих на гироскоп, не равен нулю и не действует кратковременно, ось гироскопа начинает поворачиваться в пространстве. Движение оси гироскопа под действием момента внешних сил называется процессией.
Если момент внешних сил, действующих на гироскоп, не равен нулю и не действует кратковременно, ось гироскопа начинает поворачиваться в пространстве. Движение оси гироскопа под действием момента внешних сил называется процессией.
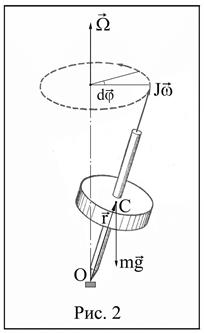
На гироскоп, изображенный на рис.2, действует момент силы тяжести 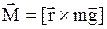 , где
, где 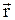 – радиус-вектор, проведенный из точки О в точку приложения силы тяжести
– радиус-вектор, проведенный из точки О в точку приложения силы тяжести 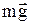 . Под действием момента силы тяжести гироскоп совершает прецессию: его ось описывает в пространстве конус. Угловая скорость прецессии равна
. Под действием момента силы тяжести гироскоп совершает прецессию: его ось описывает в пространстве конус. Угловая скорость прецессии равна
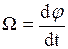 (1)
(1)
где 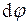 – угол поворота оси гироскопа за время
– угол поворота оси гироскопа за время 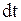 .
.
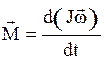 или
или 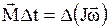
Гироскопические силы
Обратимся к простому опыту: возьмем в руки вал АВ с насаженным на него колесом С (рис. 10). Пока колесо не раскручено, не представляет никакого труда поворачивать вал в пространстве произвольным образом. Но если колесо раскручено, то попытки повернуть вал, например, в горизонтальной плоскости с небольшой угловой скоростью 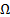 приводят к интересному эффекту: вал стремится вырваться из рук и повернуться в вертикальной плоскости; он действует на кисти рук с определенными силами RA и RB (рис. 10). Требуется приложить ощутимое физическое усилие, чтобы удержать вал с вращающимся колесом в горизонтальной плоскости.
приводят к интересному эффекту: вал стремится вырваться из рук и повернуться в вертикальной плоскости; он действует на кисти рук с определенными силами RA и RB (рис. 10). Требуется приложить ощутимое физическое усилие, чтобы удержать вал с вращающимся колесом в горизонтальной плоскости.
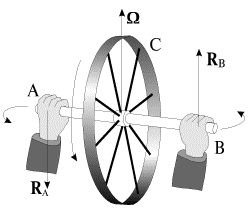
Рис. 10
Рассмотрим эффекты, возникающие при вынужденном вращении оси гироскопа, более подробно. Пусть ось гироскопа будет укреплена в U-образной раме, которая может поворачиваться вокруг вертикальной оси OO' (рис. 11). Такой гироскоп обычно называют несвободным - его ось лежит в горизонтальной плоскости и выйти из нее не может.
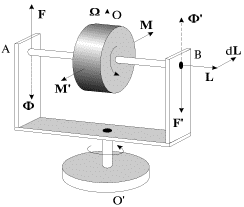
Рис. 11
Раскрутим гироскоп вокруг его вокруг его оси симметрии до большой угловой скорости (момент импульса L) и станем поворачивать раму с укрепленным в ней гироскопом вокруг вертикальной оси OO' с некоторой угловой скоростью 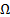 как показано на рис. 11. Момент импульса L, получит при этом приращение dL которое должно быть обеспечено моментом сил M, приложенным к оси гироскопа. Момент M, в свою очередь, создан парой сил
как показано на рис. 11. Момент импульса L, получит при этом приращение dL которое должно быть обеспечено моментом сил M, приложенным к оси гироскопа. Момент M, в свою очередь, создан парой сил 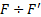 возникающих при вынужденном повороте оси гироскопа и действующих на ось со стороны рамы. По третьему закону Ньютона ось действует на раму с силами
возникающих при вынужденном повороте оси гироскопа и действующих на ось со стороны рамы. По третьему закону Ньютона ось действует на раму с силами 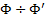 (рис. 11). Эти силы называются гироскопическими; они создают гироскопический момент
(рис. 11). Эти силы называются гироскопическими; они создают гироскопический момент 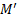 . Появление гироскопических сил называют гироскопическим эффектом. Именно эти гироскопические силы мы и чувствуем, пытаясь повернуть ось вращающегося колеса (рис.10).
. Появление гироскопических сил называют гироскопическим эффектом. Именно эти гироскопические силы мы и чувствуем, пытаясь повернуть ось вращающегося колеса (рис.10).
Гироскопический момент нетрудно рассчитать. Положим, согласно элементарной теории, что
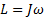
где J- момент инерции гироскопа относительно его оси симметрии, а ω - угловая скорость собственного вращения. Тогда момент внешних сил, действующих на ось, будет равен
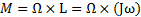
где ω - угловая скорость вынужденного поворота (иногда говорят: вынужденной прецессии). Со стороны оси на подшипники действует противоположный момент
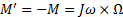
Таким образом, вал гироскопа, изображенного на рис. 11, будет прижиматься кверху в подшипнике В и оказывать давление на нижнюю часть подшипника А.
Направление гироскопических сил можно легко найти с помощью правила, сформулированного Н.Е. Жуковским: гироскопические силы стремятся совместить момент импульса L гироскопа с направлением угловой скорости вынужденного поворота. Это правило можно наглядно продемонстрировать с помощью устройства, представленного на рис. 12.
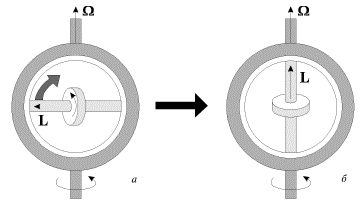 Рис. 12
Рис. 12
Ось гироскопа закреплена в кольце, которое может свободно поворачиваться в обойме. Приведем обойму во вращение вокруг вертикальной оси с угловой скоростью 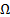 (вынужденный поворот), и кольцо с гироскопом будет поворачиваться в обойме до тех пор, пока направления L и
(вынужденный поворот), и кольцо с гироскопом будет поворачиваться в обойме до тех пор, пока направления L и 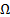 не совпадут. Такой эффект лежит в основе известного магнитомеханического явления - намагничивания железного стержня при его вращении вокруг собственной оси - при этом спины электронов выстраиваются вдоль оси стержня (опыт Барнетта).
не совпадут. Такой эффект лежит в основе известного магнитомеханического явления - намагничивания железного стержня при его вращении вокруг собственной оси - при этом спины электронов выстраиваются вдоль оси стержня (опыт Барнетта).
Гироскопические усилия испытывают подшипники осей быстро вращающихся частей машины при повороте самой машины (турбины на корабле, винта на самолете и т.д.). При значительных величинах угловой скорости вынужденной прецессии 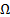 и собственного вращения
и собственного вращения 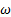 а также больших размерах маховика эти силы могут даже разрушить подшипники. Рассмотрим некоторые примеры проявления гироскопических сил.
а также больших размерах маховика эти силы могут даже разрушить подшипники. Рассмотрим некоторые примеры проявления гироскопических сил.
Пример. Легкий одномоторный самолет с правым винтом совершает левый вираж (рис. 13). Гироскопический момент передается через подшипники А и В на корпус самолета и действует на него, стремясь совместить ось собственного вращения винта (вектор 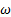 ) с осью вынужденной прецессии (вектор
) с осью вынужденной прецессии (вектор 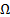 ). Самолет начинает задирать нос кверху, и летчик должен "дать ручку от себя", то есть опустить вниз руль высоты. Таким образом, момент гироскопических сил будет компенсирован моментом аэродинамических сил.
). Самолет начинает задирать нос кверху, и летчик должен "дать ручку от себя", то есть опустить вниз руль высоты. Таким образом, момент гироскопических сил будет компенсирован моментом аэродинамических сил.
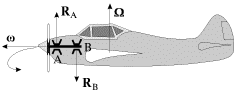
Рис. 13
| <== предыдущая лекция | | | следующая лекция ==> |
| Английское искусство XVIII в. | | | Лекция геоморфология |
Дата добавления: 2015-12-17; просмотров: 4180;
