ТЕПЛООБМЕННЫХ АППАРАТОВ
ОСНОВЫ ТЕПЛОВОГО РАСЧЁТА
Классификация теплообменных аппаратов
Сведения, полученные при рассмотрении процессов теплопроводности, конвекции и излучения, используются при расчёте сложных видов теплообмена – теплоотдачи и теплопередач, которые наблюдаются в теплообменных аппаратах.
Теплообменным аппаратом или теплообменником называется техническое устройство, служащее для передачи тепла от одного теплоносителя к другому. В качестве теплоносителей могут выступать газы, капельные жидкости, жидкие металлы, запылённые потоки и т. д.
По принципу действия различают:
1. Рекуперативные теплообменники, в которых теплота от одного теплоносителя к другому передаётся через разделяющую их стенку. В них процесс переноса тепла осуществляется путём теплопередачи без физического контакта теплоносителей.
2. Регенеративные теплообменники, в которых одна и та же поверхность омывается то горячим, то холодным теплоносителем. Перенос тепла осуществляется теплообменом с поверхностью при нестационарном режиме.
3. Смесительные теплообменники, в которых перенос тепла происходит путём их непосредственного контакта и смешивания.
Основные положения теплового расчёта
рекуперативных теплообменников
Различают два вида тепловых расчётов теплообменных аппаратов – проектный и поверочный. При проектном расчёте искомой величиной является поверхность теплообмена F, зная которую в дальнейшем осуществляют конструктивное оформление теплообменного аппарата. При поверочном расчёте поверхность теплообмена F известна. Целью поверочного расчёта является определение количества переданного тепла Q и температуры теплоносителей на выходе из теплообменника.
В основе любого теплового расчёта лежат два уравнения: теплового баланса и теплопередачи. Рассмотрим эти два уравнения применительно к рекуперативным теплообменникам в пренебрежении потерями давления для стационарного режима.
Уравнение теплового баланса рекуперативного теплообменника
Пусть массовый расход горячего теплоносителя G1, а холодного – G2. Если на некотором элементарном участке теплообмена энтальпия горячего теплоносителя изменилась на 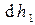 , а холодного – на
, а холодного – на 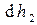 , то при отсутствии тепловых потерь
, то при отсутствии тепловых потерь 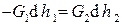 или для всего теплообменника
или для всего теплообменника
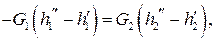
где величины с одним штрихом относятся к входному сечению теплообменника для теплоносителя, а величины с двумя штрихами – к выходному сечению теплообменника для теплоносителя.
В отсутствие фазовых переходов (кипения или конденсации) тепловой баланс запишется в виде
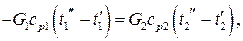
где в качестве изобарных теплоёмкостей следует брать средние величины в соответствующем интервале температур.
Уравнение теплопередачи
В случае теплопередачи от одного теплоносителя к другому через разделяющую их поверхность передаваемый тепловой поток (тепловая мощность) в строгой постановке должен определяться поверхностным интегралом I рода
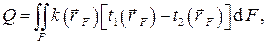
где 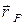 – координаты точек поверхности;
– координаты точек поверхности; 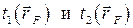 – локальные значения температур греющего и нагреваемого теплоносителей соответственно;
– локальные значения температур греющего и нагреваемого теплоносителей соответственно; 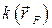 – локальное значение коэффициента теплопередачи. В случае цилиндрической теплопередающей поверхности (что имеет место в подавляющем большинстве рекуперативных теплообменников) тепловая мощность теплообменника запишется в виде
– локальное значение коэффициента теплопередачи. В случае цилиндрической теплопередающей поверхности (что имеет место в подавляющем большинстве рекуперативных теплообменников) тепловая мощность теплообменника запишется в виде
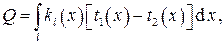
где 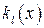 – коэффициент теплопередачи, приходящийся на единицу длины трубы теплообменника. Методы расчёта коэффициента теплопередачи рассмотрены в предыдущих разделах курса. В практических расчётах коэффициент теплопередачи относят ко всей теплообменной поверхности, подразумевая под ним среднеинтегральную величину, т. е.
– коэффициент теплопередачи, приходящийся на единицу длины трубы теплообменника. Методы расчёта коэффициента теплопередачи рассмотрены в предыдущих разделах курса. В практических расчётах коэффициент теплопередачи относят ко всей теплообменной поверхности, подразумевая под ним среднеинтегральную величину, т. е.
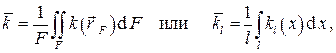
а входящие в выражения для коэффициентов теплопередачи теплофизические величины берут из справочных материалов по среднеарифметической температуре теплоносителя на входе в теплообменник и на выходе из него, т.е.
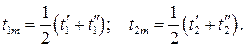
В дальнейшем будем рассматривать только рекуперативные теплообменники трубчатого исполнения, т.е. для вычисления тепловой мощности будем использовать формулу , которую перепишем в виде
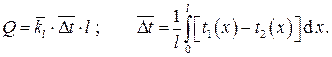
Постановка задачи теплового расчёта
рекуперативного теплообменника типа «труба в трубе»
Разность температур 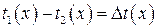 , входящая под интеграл в носит название локального температурного напора. Чтобы вычислить значение среднеинтегрального температурного напора, поставим задачу теплового расчёта простейшего рекуперативного теплообменника типа “труба в трубе“ (рис. 11.1) с теплоносителями греющим (1) и нагреваемым (2) без фазовых переходов и без тепловых потерь через внешнюю оболочку теплообменника (обечайку). Будем считать также, что оба теплоносителя движутся в одну сторону, как это показано на рисунке. Такая схема движения теплоносителей носит название прямотока.
, входящая под интеграл в носит название локального температурного напора. Чтобы вычислить значение среднеинтегрального температурного напора, поставим задачу теплового расчёта простейшего рекуперативного теплообменника типа “труба в трубе“ (рис. 11.1) с теплоносителями греющим (1) и нагреваемым (2) без фазовых переходов и без тепловых потерь через внешнюю оболочку теплообменника (обечайку). Будем считать также, что оба теплоносителя движутся в одну сторону, как это показано на рисунке. Такая схема движения теплоносителей носит название прямотока.
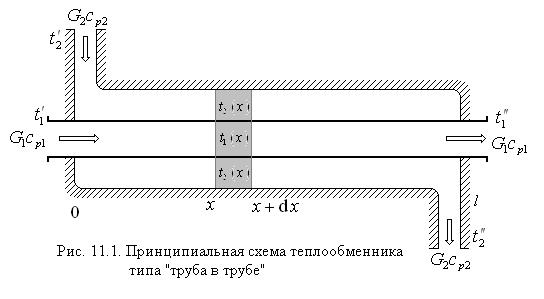
Для элемента длины dx трубы уравнения теплового баланса и теплопередачи записываются соответственно
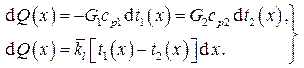
Эти уравнения приводят к дифференциальному уравнению первого порядка для локального температурного напора
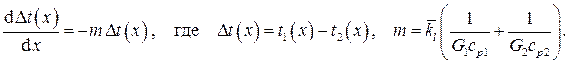
Решение этого уравнения при условии на входе в теплообменник
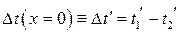
есть (см. рис. 11.2)
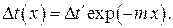
Среднеинтегральное значение температурного напора будет тогда
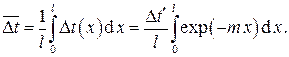
Интегрирование и последующие алгебраические преобразования дают
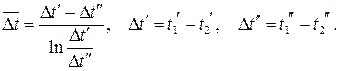
Это выражение носит название среднелогарифмического температурного напора.
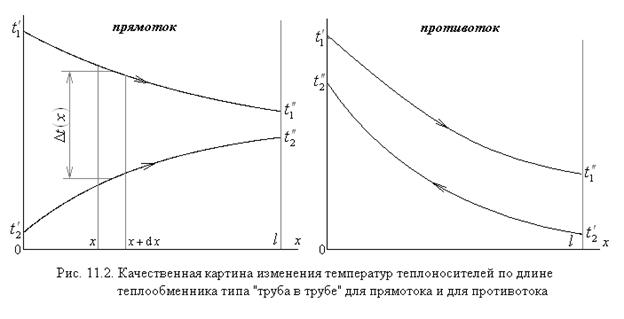
В случае так называемого противотока, т. е. в случае когда теплоносители движутся в противоположных направлениях, схема теплового расчёта остаётся такой же, как и в случае прямотока, за исключением вычисления среднелогарифмического температурного напора , где в качестве разностей температур теплоносителей слева и справа следует подставлять величины
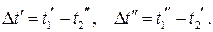
| <== предыдущая лекция | | | следующая лекция ==> |
| | | Класс Птицы насчитывает около 9000 видов. |
Дата добавления: 2015-12-17; просмотров: 1488;
