Замедпяющие системы

Назначение замедляющих систем. Эффективная отдача энергии электронами бегущей волне, как было выяснено ранее, происхо­дит при скорости электронов, несколько превышающей фазовую скорость волны. Очевидно, фазовая скорость бегущей волны в линии передачи должна быть меньше скорости света, являющейся предельной для электронов. Иными словами, линия передачи долж­на быть сконструирована так, чтобы бегущая волна в ней распро­странялась замедленно по отношению к волне, распространяющейся в свободном пространстве. Такие линии передачи называются за­медляющими системами (ЗС). Отношение скорости света к фазовой скорости бегущей волны в системе называется коэффициентом за­медления, значения которого для типовых ЗС лежат в пределах 5-30. Необходимость замедления бегущей волны в несколько раз вызвана стремлением использовать относительно небольшие ускоряющие напряжения электронного потока, обусловливающие необходимую скорость электронов. Так, замедлению в 15 раз соответствует ускоряющее напряжение, примерно равное 1100 В, а замедлению в 5 раз - 10 кВ.

Типы замедляющих систем. Замедляющая система предназначе­на для осуществления взаимодействия бегущей волны с электрон­ным потоком, поэтому одним из основных требований к системе является наличие в ней продольной составляющей электрического поля (вдоль оси х), взаимодействующей с электронами.

Наиболее широко распространены в приборах СВЧ ЗС с перио­дической структурой. Способ получения замедленных волн в та­ких ЗС основан на зависимости типа возникающих волн (конфигу­рации поля) и их фазовой скорости от граничных условий, т.е. от конфигурации поверхности элементов ЗС. Чаще всего использу­ются периодические ЗС, состоящие из отдельных повторяющихся по конструкции ячеек. Длину ячейки или расстояние между центрами ячеек h принято называть периодом структуры.

Замедляющая система может быть однородной и неоднородной. Однородной ЗС называется система, в которой период структуры намного меньше длины волны в ЗС. Если период структуры соизме­рим с длиной волны в ЗС, то такая ЗС называется неоднородной.

Типичным представителем однородных ЗС является

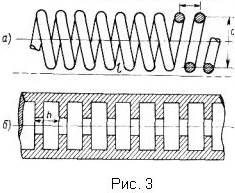
спираль из тонкой проволоки с постоянными радиусом и шагом намотки, при­чем шаг намотки намного меньше длины волны, распространяющей­ся вдоль оси х (рис.За) Замедление волны в спирали можно представить упрощенно как результат последовательного перемещения волны вдоль витков спи­рали, вследствие чего поступательное переме­щение фронта волны вдольоси х окажется замедленным примерно в число раз, равное отношению длины L провода, из которого намотана спираль, к длине l спирали. Иначе говоря,

c / v_ф ≈ L / l ≈ πd / h

где h - шаг спирали; d - диаметр спирали. Однородная спираль интересна тем, что распространяющаяся в ней волна имеет синусоидальную зависимость от координаты x.

В случае неоднородных систем структура поля вдоль оси x имеет более сложный вид, зачастую резко отличающийся от синусоидального

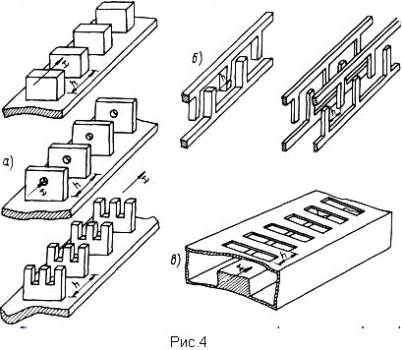
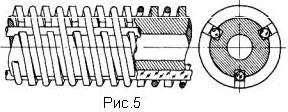
Примеры некоторых конструкций замедляющих систем показа­ны на рис.3 - 5: на рис.3б - диафрагмированный вол­новод, на рис.4а - ЗС типа "гребенка", на рис.4б -встречно-штыревые ЗС, на рис.4в - ЗС лестничного типа и на рис.5 - ЗС типа "винт со спиралью".

Структура поля в неоднородных ЗС. Неоднородные ЗС получи­ли широкое распространение по той причине, что они наиболее полно отвечают ряду требований, которые предъявляются к ЗС. В частности, в неоднородных ЗС может быть получена большая про­дольная составляющая электрического поля, от которой зависит эффект взаимодействия поля с электронным потоком.

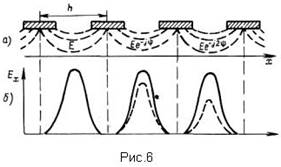
Неоднородные ЗС имеют длину ячейки, сравнимую с длиной вол­ны в ЗС, вследствие чего поле в двух соседних ячейках имеет конечную разность фаз, а вдоль оси ЗС - несинусоидальный ха­рактер. Пространственная периодичность ЗС приводит к тому, что поле во всех ячейках идентично, но сдвинуто на фазовый угол ψ в каждой последующей ячейке по отношению к предыдущей (рис.6а). В общем случае продольная составляющая электричес­кого поля

E_x(x+h, y, z) = E_x(x, y, z) exp (-jψ). (2)

Для распределения поля только на оси ЗС (в месте прохождения электронного потока) выражение (2) можно упростить . E_x (x+h) = E_x(x)exp (-jψ). (3)

На рис.6б показано распределение амплитуд напряженнос­ти поля Е_{x_} вдоль оси х; штриховой линией показано распре­деление поля Е_x в фиксированный момент времени для случая π >> ψ >0..

Сложная структура поля в неоднородной ЗС, в общем случае отличающаяся резко несинусоидальным характером вдоль оси х, во времени изменяется по синусоидальному закону, если ЗС воз­буждается лишь на одной частоте ω. С учетом этого обстоя­тельства продольная составляющая

поля в любой точке вдоль оси x ЗС может быть представлена в виде E (х,t)=Е (х) ехр [j (ωt-βx)], где коэффициент фазы β связан со сдвигом фаз ψ соотношением

Ψ = β h. (4)Неоднородную периодическую ЗС можно рассматривать как це­почку, состоящую из одинаковых звеньев с сосредоточенными постоянными и имеющую, как известно,

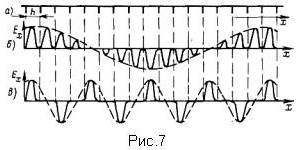
свойства фильтров. Иными словами, ячейка ЗС может быть представлена эквивалентным поло­совым фильтром. Фазовый сдвиг ψ в ячейке может изменяться в пределах 0 < І.ψ І < π, т.е. в пределах физической различимос­ти дискретных разностей фаз. Граничным значениям угла ψ (0,π) соответствуют верхняя и нижняя граничные частоты полосы про­пускания системы. На рис.7 в качестве примера показано распределение по­ля вдоль оси х в некоторой неоднородной ЗС (рис.7а) в фиксированный момент времени при двух различных фазовых сдвигах в соседних ячейках: ψ₀ = π / 8 (рис.7б) и ψ = π / 2 (рис.7в)

.

Пространственные гармоники. Электрическое поле в ЗС может быть представлено в виде суммы отдельных бегущих волн - прост­ранственных гармоник, распространяющихся вдоль оси x с различными фазовыми скоростямиПредположим, что ЗС простирается неограниченно вдоль коор­динаты х или согласована с нагрузкой на конце и не имеет по­терь. Тогда выражение для продольной составляющей сложного по­ля бегущей волны вдоль оси х будет иметь вид

E_x (х,t)=Е_x (х) ехр [j (ωt-βx)], (5)

где Е_x (х) - периодическая функция с пространственным пери­одом h , характеризующая зависимость амплитуды поля от коор­динаты x.

Как известно, любая периодическая функция некоторого ар­гумента x. может быть представлена гармоническим рядом Фурье. Разложение выражения (7) в ряд Фурье по x для фиксированно­го момента времени (t = 0) позволяет получить бесконечно большое множество так называемых пространственных гармоник.

Любая пространственная гармоника, таким образом, может быть записана в виде

E_xk (х,t)=Е_xkm (х) ехр [j (ωt-β_kx)],

где β_k = β₀ + 2 kπ / h (6)

В выражении (6) β_k представляет собой коэффициент фазы k -ой гармоники. Умножив левую и правую части в выражении (6) на h , получим связь между фазовым углом в соседних ячейках для k -ой и нулевой гармоник:

ψ_k=ψ₀+2kπ. (7)

Таким образом, поле в ЗС, имеющее сложную структуру, может быть представлено суммой пространственных гармоник, коэффици­ент фазы которых определяется выражением (6), а фазовый сдвиг в соседних ячейках - выражением (7). Это означает, что фазовые скорости пространственных гармоник различны, так как

β_k = ω / v_фk, (8)

где v_фk фазовая скорость k -й гармоники.

Скорость v_фk можно найти, использовав соотношения (8) и (6):

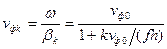(9)

где f - частота колебаний в ЗС.

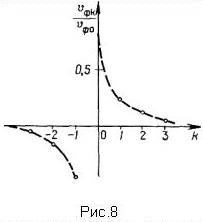
Типичная зависимость фазовой скорости пространственных гармоник от их номера показана на рис.16.8 для случая v_ф0 > 0.

Как видно из формул (9) и (6), пространственные гармоники в зависимости от номера могут иметь либо положитель­ную

фазовую скорость, либо отрицательную. Первые называются прямыми гармониками, а вторые - обратными Гармоника с номером k =0 называется основной. Она может иметь фазовую скорость как положительную, так и отри­цательную в зависимости от на­правления распространения энер­гии в ЗС, характеризуемого зна­ком групповой скорости.

Групповая скорость, как известно, определяется выражением v_Г = dω /dβ.

Продифференцировав выражение (6) по частоте ω, нетрудно заметить, что v_Г = dω / dβ_k = dω / dβ_0, т.е. групповая скорость всех пространственных гармоник одна и та же. Этого и следовало ожидать, так как пространственные гармоники не могут существовать раздельно. Они являются эле­ментами разложения действительно существующего поля в ЗС, ха­рактеризуемого одним значением групповой скорости.

Фазовая скорость прямых гармоник совпадает по знаку с групповой скоростью. Обратные гармо­Ники имеют знак фазовой скорости, противополож­ный знаку групповой скорости.

Физический смысл прямых гармоник не нуждается в пояснении. Что же касается обратных гармоник, то их физический смысл мож­но уяснить из рассмотрения фазового сдвига в двух соседних ячейках. Предположим, что этот фазовый сдвиг для основной гар­моники превышает π и равен 2π – ψ₀ , причем ψ₀ < π . Угол ψ₀ на основе выражения (3) можно рассматривать как отрицатель­ный, так как еxр[-j (2π-ψ₀)] = ехр[-j(-ψ₀)], а это означает, что фаза гармоники в последующей ячейке опережает фазу этой же гармоники в предыдущей ячейке на угол ψ₀ , т.е. можно записать ψ₀ < 0, что эквивалентно неравенству v_ф0 < 0. Иными словами, в рас­смотренном примере вдоль ЗС распространяется основная гармони­ка, являющаяся обратной. Аналогичные рассуждения справедливы для любой пространственной гармоники.

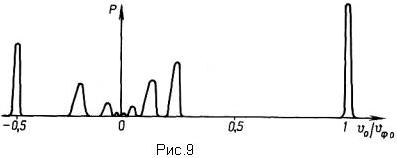
Реальность существования в ЗС прямых и обратных простран­ственных гармоник, бегущих навстречу друг другу, доказывается возможностью осуществления анализатора, построенного по ско­ростному принципу. Действительно, направив электронный поток вдоль оси ЗС, при изменении его скорости v₀ можно обнаружить увеличение энергии электромагнитного поля в ЗС вблизи значений v_фk ≈ v₀ , что объясняется взаимодействием потока и k -ой пространственной гармоники (рис.9). При этом увеличивается энергия всего поля, т.е. амплитуды всех гармоник увеличиваются пропорционально, так как пространственные гармоники не могут существовать каждая в отдельности. Соотношение амплитуд гармо­ник определяется параметрами ЗС. Как правило, амплитуда гармо­ники с увеличением номера гармоники убывает, а поэтому умень­шается и степень взаимодействия гармоники с электронным пото­ком, а следовательно, и суммарная энергия поля.

Фазовая скорость любой пространственной гармоники всегда меньше или равна по абсолютной величине фазовой скорости ос­новной (нулевой) пространственной гармоники, т.е. Iv_фk‌ ≤ ‌ v_ф0 ‌|.

Действительно, фазовый сдвиг в двух соседних ячейках для любой пространственной гармоники больше фазового сдвига для основной гармоники на 2kπ , а это свидетельствует о меньшей по абсолютной величине фазовой скорости k-ой пространст­венной гармоники.

Основные характеристики замедляющих систем. Фазовая ско­рость пространственных гармоник в ЗС зависит от частоты коле­баний. Это явление носит название дисперсии, а зависимость v (f) называется дисперсионной характеристикой. Дисперси­онные свойства ЗС важно знать по той причине, что они опреде­ляют возможность использования данной ЗС в том или ином при­боре. Характер зависимости фазовой скорости от частоты опре­деляет необходимое изменение скорости электронов потока, а следовательно, и изменение ускоряющего напряжения в диапазо­не частот (так как v_о≈ v_фk). Если, например, фазовая скорость пространственной гармоники, взаимодействующей с потоком элект­ронов, почти не изменяется с изменением частоты, то и необхо­димое ускоряющее напряжение, управляющее скоростью электро­нов, практически не изменяется в диапазоне частот.

Пространственные гармоники ЗС обладают неодинаковой дис­персией. Групповая скорость для всех гармоник на данной частоте может быть определена в функции фазовой скорости k - ой гармоники:

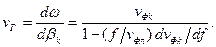(10)

Групповая скорость обычно считается положительной. Прямые гармоники имеют фазовую скорость, совпадающую по направлению с групповой скоростью. Фазовая скорость обратных гармоник противополож­на по знаку групповой скорости.

В зависимости от знака фазовой скорости дисперсия может быть положительной (v_фk <0) и отрицательной (v_фk >0) . Все пря­мые гармоники имеют положительную дисперсию, а обратные - от­рицательную, так как v_г > 0.

Характер зависимости фазовой скорости пространственной гармоники от частоты определяется производной d ‌v_фk| / df , кото­рая может иметь различный знак. Принято называть дисперсию нор­мальной, если d ‌v_фk| / df < 0 , и аномальной, если d ‌v_фk| / df > 0.

Прямые гармоники могут иметь и нормальную, и аномальную дисперсию, а обратные - только аномальную.

Если известна дисперсионная характеристика для основной пространственной гармоники, то в соответствии с выражением

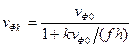(11)

можно построить дисперсионные характеристики для всех прост­ранственных гармоник. Поэтому часто ЗС характеризуют диспер­сией основной гармоники. Это тем более оправдано, что в боль­шинстве случаев используется именно основная гармоника. Таким образом, говорят, что ЗС обладает либо положительной, либо от­рицательной дисперсией, в зависимости от того, какова диспер­сия основной

гармоники. Но при этом другие пространственные гармоники ЗС могут иметь дисперсию, отличную от дисперсии основной гармоники. На рис.10 показаны дисперсионные характеристики неко­торой ЗС с положительной дисперсией. Дисперсия основной (в данном случае прямой) гармоники - нормальна, а дисперсия пря­-

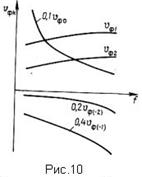
мых (исключая основную) и обратных гармоник - аномальна. Ины­ми словами, абсолютные значения фазовых скоростей всех прост­ранственных гармоник, исключая основную, растут с увеличением частоты

Зависимость групповой скорости от частоты характеризует широкополосность ЗС. Чем меньше изменяется групповая скорость с изменением частоты, тем полоса частот ЗС шире. Действительно, для эффективного взаимодействия электронного потока с бе­гущей волной необходимо обеспечить примерное равенство скорос­ти электронов и фазовой скорости волн. Если дисперсия дан­ной пространственной гармоники выражена сильно, то при одной и той же скорости потока электронов синхронизм с волной будет наблюдаться лишь в небольшой области частот, как это следует из выражения (10).

Иными словами, для эффективного использования ЗС в кон­кретном приборе необходимо знать характер дисперсии фазовой скорости пространственных гармоник.

Дисперсионные характеристики чрезвычайно важны при

использовании ЗС в приборах типа ЛБВ, так как они определяют харак­тер взаимодействия электронного потока с соответствующей гар­моникой электрического поля. Интенсивность взаимодействия бу­дет определяться величиной соответствующей гармонической составляющей. Поэ­тому не менее важной характеристикой ЗС является параметр, определяющий степень взаимодействия электронного потока с составляющей поля, имеющей фазовую скорость, примерно равную скорости электронов. В качестве такого параметра, позволяющего провести сравнение ЗС, часто используется сопротивление связи R_{CB k} , определяемое соотношением между квадратом амплитуды Е_xkm k -ой гармоники и общим потоком мощности Р , проходящим через поперечное сечение ЗС:

R_{CB k} = Е_xkm / (2 β²_k Р) (12)

Амплитуда E_xkm определяется в месте расположения элект­ронного потока, а поток мощности Р учитывает суммарную мощ­ность всех пространственных гармоник поля. Чем больше амплиту­да E_xkm при одной и той же мощности Р , тем выше сопротивле­ние связи R_{CB k} , тем лучше взаимодействует поток с k -й гармоникой поля. Для расчета сопротивления связи, как видно из выражения (12), необходимо знать дисперсионные свойства ЗС, определяющие значения коэффициента фазы β_k , а также функции распределения поля в ЗС.

Интенсивность поля замедленных волн в ЗС убывает с удале­нием от ее поверхности, а соотношение амплитуд пространствен­ных гармоник определяется конструкцией ЗС. В реальных приборах электронный поток имеет конечную толщину, поэтому для более правильной оценки эффективности взаимодействия потока с полем в выражении для сопротивления связи учитывают среднеквадра­тичное значение амплитуды E_xkm по всей площади сечения элект­ронного потока.

Взаимодействие электронного потока с полем неоднородной ЗС можно рассматривать как взаимодействие с одной лишь пространственной гармоникой, фазовая скорость которой близка к скорости электронов. В этом случае справедливы рассуждения, применяв­шиеся при обсуждении взаимодействия потока с полем синусои­дальной бегущей волны. Поле определенной гармоники группирует электронный поток в сгустки, взаимодействует с ним, отбирая от потока энергию. Направления движения гармоники и потока должны быть одинаковыми. В процессе взаимодействия увеличивается ам­плитуда всех пространственных гармоник в равной степени, так как структура суммарного поля определяется конструкцией ЗС. Направление распространения энергии может и не совпадать с на­правлением электронного потока. В этом случае, как известно, поток взаимодействует с обратной гармоникой.