Вывод уравнения изгиба круглой пластины

Преобразование декартовых координат к полярным осуществляется по формулам:

, (2.1)

где 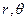- полярные координаты (рис. 2.1).

а б

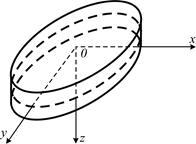
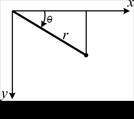
Рис. 2.1

Если принять начало радиуса полярной системы совпадающим с началом оси х декартовой системы, то формулы

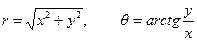
устанавливают связь координат произвольной точки на плоскости.

Производные величин 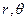легко вычислить:

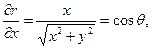
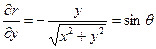, (2.2)

,

.

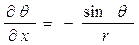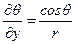На основании данных вычислений без труда находятся производные:

,

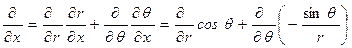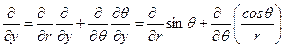, (2.3)

.

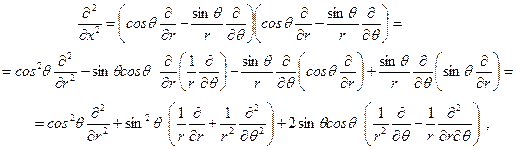
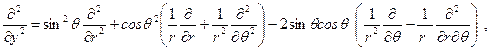
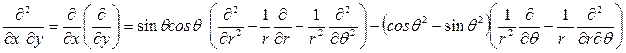Оператор Лапласа

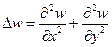
с учётом данных определений производных в полярных координатах принимает вид

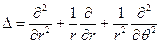. (2.4)

С его помощью левая часть уравнения изгиба пластинки в полярных координатах может быть представлена состоящей из сомножителей

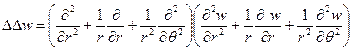. (2.5)

Приравнивая это выражение величине 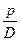, выводят уравнение изогнутой поверхности

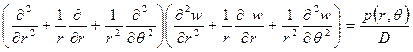. (2.6)

Здесь, как и для прямоугольной пластинки, 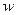обозначает прогиб произвольной точки, 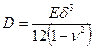- цилиндрическую жёсткость, 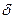- её толщину; 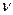- коэффициент Пуассона, 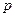- интенсивность распределённой нагрузки.

При действии симметричной нагрузки прогибы не зависят от окружной координаты. Следовательно, производные функции прогибов по 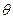в уравнении исключаются, и уравнение принимает вид

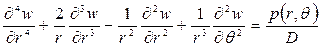. (2.7)

2.1 Интегрирование уравнения изгиба круглых пластин

Общий интеграл уравнения (2.7) можно представить как сумму частного решения и решения однородного уравнения при 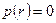, т. е.

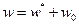. (2.8)

Частное решение в случае равномерно распределённой нагрузки очевидно -

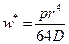. (2.9)

Решение однородного уравнения записывается в виде

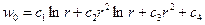, (2.10)

где 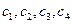- постоянные интегрирования.

Таким образом, общее решение для круговой пластинки имеет вид

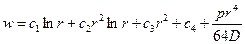. (2.11)

2.3. Определение изгибающих моментов и поперечных сил круглых пластин

Величины изгибающих моментов и поперечных сил в круглых пластинах, как и уравнение изогнутой поверхности, можно выразить в полярной системе. Формулы для них, во – первых, вполне естественны для анализа круглых пластин, а, во – вторых, необходимы при практическом решении задач на стадии формулировки краевых условий.

Формулы для изгибающих моментов и поперечных сил несложно вывести на основе известных выражений аналогичных величин в декартовых координатах (см. формулы для прямоугольных пластинок (1.6,а)). Воспользовавшись, например, определением

,

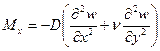после подстановки формул преобразования производных (2.3) находят моменты в радиальном направлении

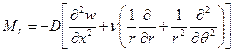. (2.12,а)

Аналогично выводят формулы и для окружных и крутящих моментов:

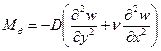
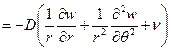, (2.12,б)

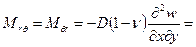
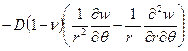. (2.12,в)

Точно также и для поперечных сил легко установить, что:

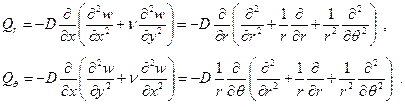(2.13)

При полярно – симметричном изгибе круглой пластинки формулы упрощаются:

Изгибающие моменты равны

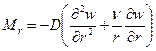, (2.14,а)

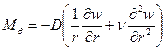. (2.14,б)

Поперечные силы -

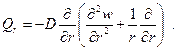(2.15)

Остальные усилия не возникают совсем

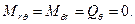(2.16)

2.4. Граничные условия для круглых пластин

А) При защемлении контура

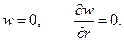(2.17)

Б) При шарнирном опирании контура

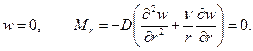(2.18)

В) На свободном контуре (при отсутствии внешних воздействий по контуру отверстия)

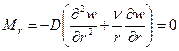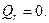, (2.19)

Г) На свободном контуре (при наличии внешних воздействий)

по наружному контуру

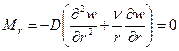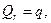, (2.20)

если нагрузка 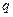распределена только на контуре;

если нагрузка 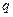распределена на внутреннем контуре (у отверстия), то должны быть выполнены следующие условия

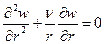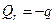, . (2.21)

2.5. Прогибы кольцевых пластин

На основе полученного решения несложно определит прогибы не только сплошных круглых пластинок, но пластинок с симметричным отверстием, т. е. кольцевых пластинок, при самых разных краевых условиях.

Рис. 2.2

В частности, для круглой пластинки с защемлённым внешним контуром и шарнирным опиранием в месте выреза (рис. 2.2) краевые условия имеют вид:

на внешнем контуре, при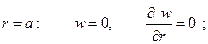

на внутреннем – при

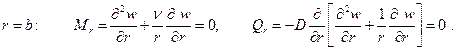
Подставив сюда выражение для прогибов (2.11), приходят к системе четырёх уравнений относительно постоянных интегрирования:

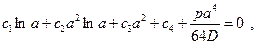
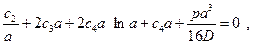
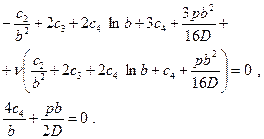
Решив систему, находят:

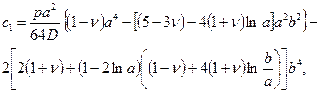
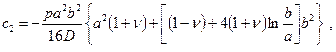
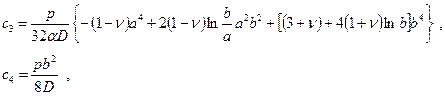
где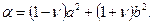

Если ещё ввести параметры:

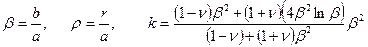
то тогда прогибы кольцевой пластинки находят по формуле

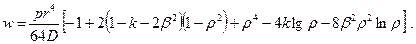
Значения моментов в пластинке при действииравномерно распределённой нагрузки р вычисляют по формулам (2.14).