ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК

ОБЩАЯ (МОМЕНТНАЯ) ТЕОРИЯ РАСЧЁТА

11.1. Уравнения состояния цилиндрической оболочки

Напряжённо–деформированное состояние коротких цилиндрических оболочек характеризуется взаимовлиянием всех внутренних усилий, возникающих при действии произвольных нагрузок. В общем случае состояние оболочки, как известно, описывается тремя группами уравнений: уравнениями равновесия (10.1), геометрическими зависимостями, взятыми для цилиндрических оболочек без каких-либо допущений, а именно:

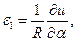
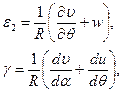
ϰ 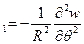, (11.1)

ϰ ,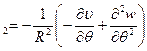

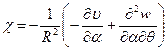
и физическими уравнениями общего вида (8.4).

Полная система данных уравнений может быть приведена к одному разрешающему уравнению в перемещениях. Последовательость сведения состоит в следующем. Сначала из условий равновесия выводятся поперечные силы; в результате из пяти условий остаются только три:

,

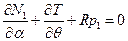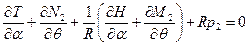, (8.2,б)

.

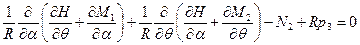После подстановки сюда величин внутренних усилий согласно (8.4) и приведения подобных членов в каждом уравнении с использованием дифференциальных операторов вида:

; ; ;

, ,

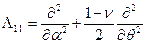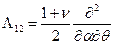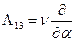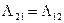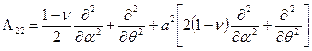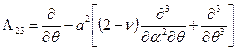, (11.2)

, , ,

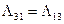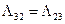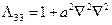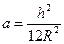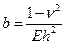постоянных и , а также параметров компонент вектора нагрузки 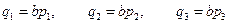система уравнений моментной теории цилиндрической оболочки в перемещениях принимает вид:

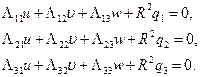(11.3)

Матрица данной системы уравнений, как явствует из определений операторов (11.2), симметрична, что является следствием теоремы Бетти. При постоянных 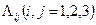, которые считаются коэффициентами системы, её можно решить как обычную систему линейных алгебраических уравнений.

Для этого, во-первых, следует переписать систему (11.3) в стандартной форме:

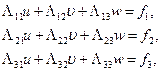
используя обозначение 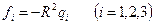. Тогда её решение проще записать в матричном виде

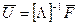. (11.4)

Здесь 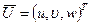обозначает вектор-столбец перемещений произвольной точки оболочки, 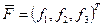- вектор нагрузки,

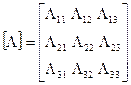
- матрица коэффициентов, состоящая из операторов 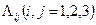(cм. (11.2)).

Более подробно выражение (11.4) записывается через определители, т. е.

,

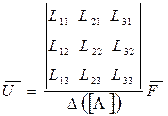где 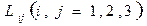- миноры определителя 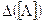; как известно, матрица, составленная из этих миноров, называется союзной матрицей.

В развёрнутой форме частное решение системы уравнений (11.3) принимает вид:

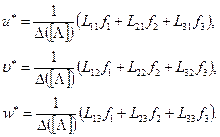
Образуя новые функции уровня нагружения оболочки

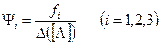, (11.5,а)

перемещения можно записать более компактно, а именно,

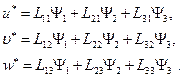(11.6)

Миноры матрицы 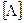находятся без труда:

(*)

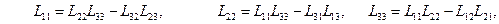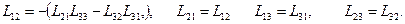
С учётом определений операторов согласно (11.2), оператор 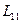, например. имеет вид:

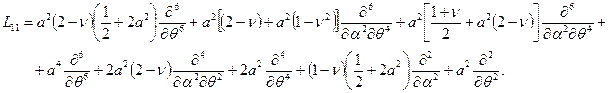
Остальные миноры имеют аналогичную структуру. В силу симметрии матрицы 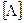справедливы равенства:

.

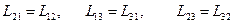Равенства (11.5,а) можно рассматривать как систему трёх уравнений, в которой неизвестными являются функции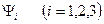

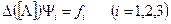, (11.5,б)

Или

.

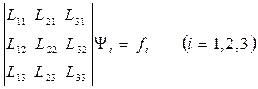Раскрыв этот определитель по правилу Саррюса и приняв во внимание определение (*) и ему подобные, выводят разрешающее уравнение моментной теории оболочки, соответствующее частному решению

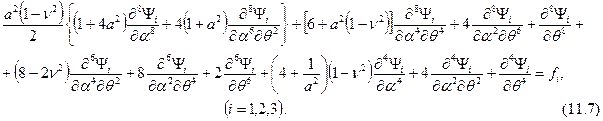
Общее решение однородной системы уравнений

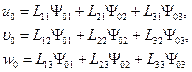(11.8)

нетрудно установить на основе (11.5,б), полагая правую часть нулевой, т.е.

.

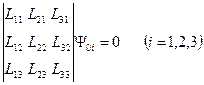Приняв, в частности, функции

,

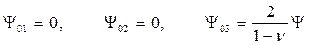согласно (11.6) находят:

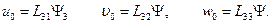
Для вывода разрешающего уравнения, соответствующего однородной системе

,

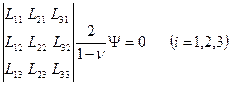достаточно, как и в решении частной задачи, развернуть определитель и учесть выражение (*) и подобные ему. В итоге приходят к разрешающему уравнению общей (моментной) теории цилиндрической оболочки

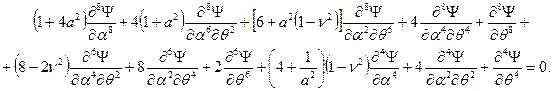(11.9)

11.2. Упрощённая форма разрешающего уравнения

Влияние вкладов ряда слагаемых, содержащихся в формулах миноров (*), на величину перемещений цилиндрических оболочек незначительно. Анализ решений многих задач показал, что слагаемыми, обладающими множителем 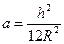, можно пренебречь (за исключением тех, которые входят в выражение оператора 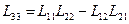). С учётом данного замечания уравнение (11.7) упрощается

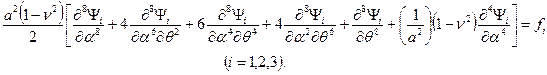
На этом же основании разрешающее уравнение общей (моментной) теории расчёта цилиндрических оболочек приводится к более краткой форме

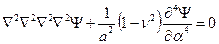, (11.10)

где неизвестной является функция уровня нагружения и деформаций .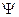

Компоненты вектора перемещения произвольной точки оболочки могут быть выражены через данную функцию по формулам:

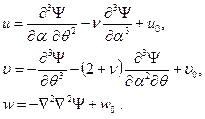(11.11)

Усилия в оболочке, удовлетворяющие условиям равновесия (8.2,б), также выражаются через функцию :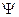

,

,

,

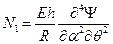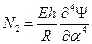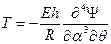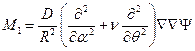, (11.12)

,

,

,

.

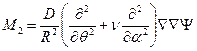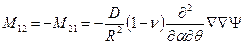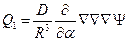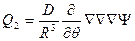Дифференциальное уравнение (11.10), представленное в форме

,

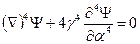где

,

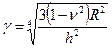эквивалентно системе четырёх уравнений второго порядка

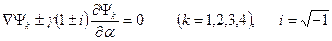. (11.13)

Если каждую функцию нагружения 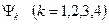выразить в виде произведения экспоненты на некоторую новую функцию напряжения :

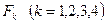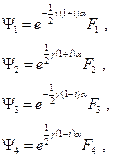
то уравнение (11.10) распадается на группу четырёх независимых уравнений

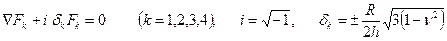. (11.14)

Подобные по форме уравнения описывают колебания мембраны. Их интегралы хорошо изучены и потому могут быть использованы при выполнении расчётов цилиндрических оболочек на статические нагрузки.

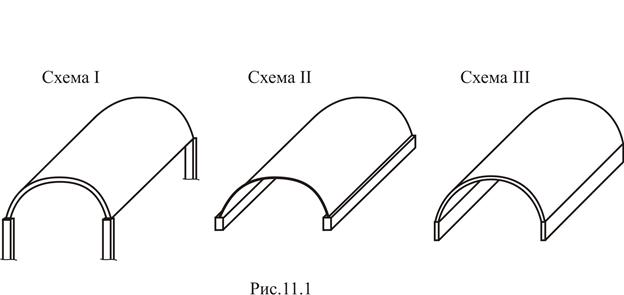
11.3. Расчёт коротких цилиндрических оболочек покрытий

Основные типы конструктивных решений покрытий представлены на рис. 11.1. Первый из них характеризуется многоволновой оболочкой, опирающейся непосредственно на колонны (схема I). Во втором случае опирание происходит через бортовой элемент – балку (схема II). В последнем варианте рассматривается оболочка, плавно переходящая в бортовой элемент, в котором возможно появление кручения (схема III). Оболочка считается короткой, если отношение длины оболочки к радиусу цилиндра не превышает единицы, т. е. при .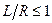

Любая внешняя нагрузка на поверхности оболочки может быть представлена в виде рядов:

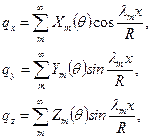(11.15)

где 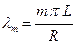. То же касается и частных решений основного уравнения:

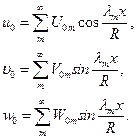(11.16)

Пользуясь данными разложениями, на основе (11.12) легко определить усилия 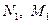и с их помощью убедиться в соблюдении граничных условий для шарнирных краёв при .

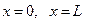Для вычисления перемещений при отсутствии внешнего воздействия

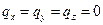функцию напряжений следует принять в виде

.

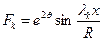Подставив её в дифференциальное уравнение (11.14), приходят к характеристическому уравнению относительно корней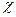

,

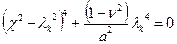где 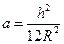- геометрический параметр, характеризующий относительную толщину оболочки.

Решив уравнение, находят:

.

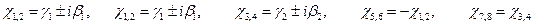Вводя новые параметры оболочки:

, ,

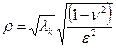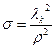вещественные и мнимые части корней можно представить в следующем виде:

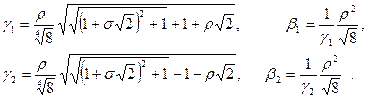
При известных корнях характеристического уравнения функция напряжений принимает вид

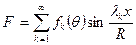, (11.17)

где

,

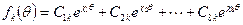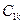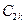, ,…- произвольные постоянные.

Вычислив производные функции напряжений, входящие в формулы для перемещений (11.11), и суммируя их с выражениями (11.16), несложно найти перемещения оболочки:

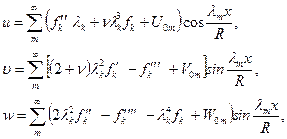(11.18)

где штрих над функцией обозначает дифференцирование по дуге, т. е. .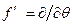

11.4. Граничные условия для расчёта коротких оболочек на вертикальные нагрузки

Для примера далее рассматривается формулировка граничных условий для оболочки, проектируемой по второй расчётной схеме (рис. 11.1,б). Приводятся расчётные формулы для случая, когда на оболочку действует равномерно распределённая по поверхности вертикальная нагрузка 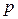, проекции которой составляют:

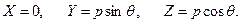
По данным значениям легко определить величины (11.15):

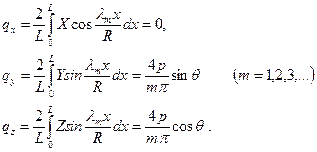, (11.19)

Частное решение, соответствующее указанному характеру нагружения, можно принять в форме:

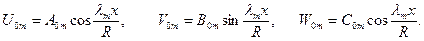(11.20)

В таком случае функцию 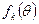, удовлетворяющую условиям симметрии относительно меридиональной плоскости 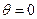, следует взять в следующем виде

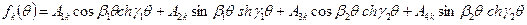, (11.21)

где 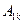, ,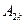…- произвольные постоянные, 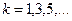; 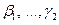- корни характеристического уравнения.

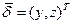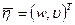Если воспользоваться обозначениями векторов перемещений оболочки в общей и локальной системах координат через и , соответственно, то связь между ними можно представить в матричном виде

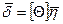, (11.22)

где

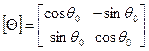
- матрица поворота вектора перемещений, 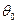- половина центрального угла оболочки [12] (рис. 11.2,а).

а б

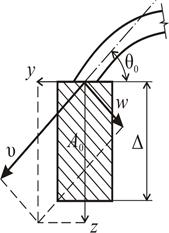
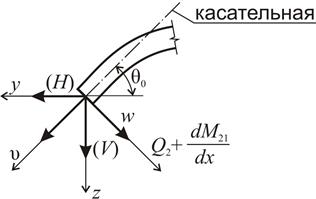
Рис. 11.2

Аналогичная зависимость между компонентами реакции 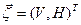на опоре и вектора обобщённых напряжений 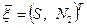записывается в аналогичной форме (рис. 11.2,б)

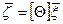, (11.23)

где 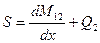- нормальная составляющая напряжений в оболочке. На основе приведенных матричных соотношений можно установить граничные условия, необходимые при интегрировании разрешающего уравнения (11.13).

В многоволновой оболочке с бортовыми элементами по II расчётной схеме (рис. 11.1), т. е. в случае наличия бортового элемента между оболочками в виде балки прямоугольного сечения с площадью 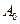, высотой 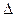и жёсткостью 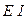, прогибы элемента можно найти из уравнения изгиба в вертикальной плоскости

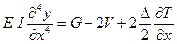, (11.24)

где 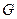- погонный вес балки, 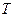- сдвигающее усилие в оболочке на её кромке, направленное вдоль оси балки. Последнее слагаемое в уравнении (11.24) отражает разность уровней боковой грани срединной поверхности оболочки на контуре и оси балки.

Очевидно, на стыке оболочек вертикальная составляющая реакции и вес элемента должны быть уравновешены 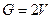. Отсюда следует, что согласно (11.20) вес балки можно разложить в ряд

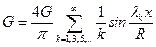. (11.25).

Кроме того, необходимо принять во внимание и зависимость между деформациями оболочки и балки в уровне верха последней

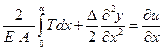. (11.26)

Вследствие симметрии конструкции в месте сопряжения оболочек горизонтальные перемещения балки, которые в общем случае находятся по формуле (11.22)

,

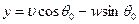отсутствуют. Следовательно, перемещения оболочки в этом месте в направлении касательной связаны с её прогибами

.

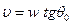Одновременно с этим угол поворота 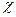кромки оболочки при 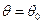, определяемый выражением (11.1), также равен нулю. Поэтому справедливо ещё и соотношение вида

.

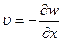Составив граничные условия, переходят к определению коэффициентов 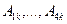функции (11.21). Функция напряжений 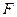находится из решения системы уравнений (11.24) и (11.26). Зная её, по формулам (11.18) определяют перемещения оболочки, а по формулам (11.12) – внутренние усилия.

В частности, для оболочки с пролётом 11,8 м и радиусом срединной поверхности 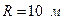(длиной 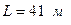) при действии нагрузки 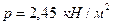построены эпюры усилий 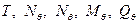, показанные на эпюрах (рис. 11.3). Погонный вес балки составляет G 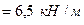. Если при расчёте цилиндрической оболочки ограничится безмоментной (мембранной) теорией, то соответствующие усилия оказываются значительно меньшими (см. пунктирные линии на эпюрах).

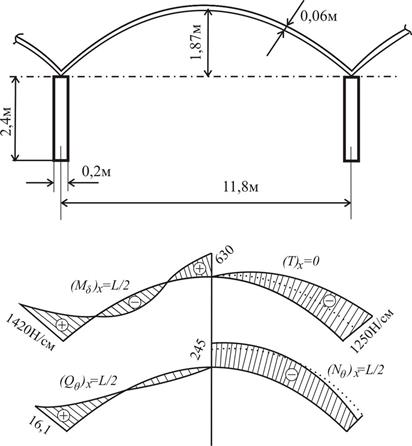
Рис. 11.3

Влияние высоты бортовой балки на внутренние усилия в цилиндрических оболочках при различных отношениях пролёта к длине подробно рассматривается в работе Цетыркина И. Е. [19].

При проектировании коротких цилиндрических оболочек рекомендуется пользоваться таблицами расчётных значений внутренних усилий, помещёнными в справочной литературе [1], [17].