Уравнения состояния цилиндрической оболочки по полумоментной теории. Принятые гипотезы расчёта

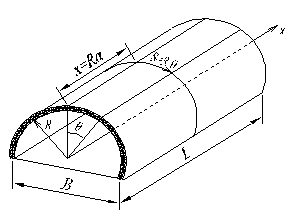
В предыдущей лекции было отмечено, что длинные цилиндрические оболочки, закреплённые на продольных кромках, при неравномерной или несимметричной нагрузке работают в основном на изгиб в поперечном направлении (рис. 10.1,а). Это означает, что в таком случае в качестве расчётной модели оболочки можно рассматривать множество элементарных полос в виде арок, соединённых между собой в продольном направлении связями-стерженьками, способными воспринимать только продольные и сдвигающие усилия данного направления (рис. 10.1,б). По этой причине изгибающие и крутящие моменты 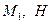, а следовательно, и поперечные силы 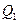в условиях равновесия оболочек (8.2,а) следует положить равными нулю. Это допущение подтверждается экспериментами, в которых отмечается незначительная роль указанных усилий в передаче внешней нагрузки на диафрагмы, устанавливаемые в торцах оболочки.

а

б

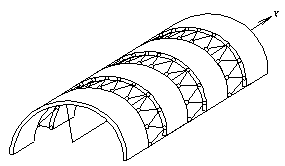
Рис. 10.1

С учётом этого условия при анализе равновесия цилиндрической оболочки по полумоментной теории следует решить систему следующих уравнений:

,

,

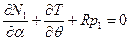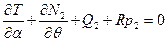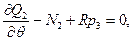(10.1)

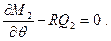
Эти уравнения, содержащие пять неизвестных усилий 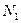, , 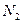, , 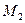, 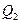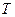получены из общих условий равновесия элемента оболочки (6.2). На рис. 10.2 элемент показан вместе с рассматриваемыми усилиями.

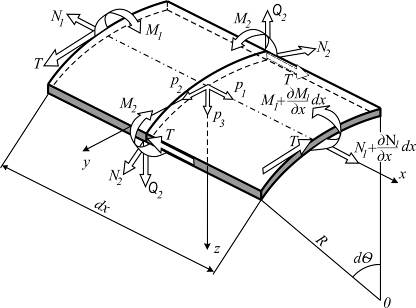
Рис. 10.2

Подобное напряжённое состояние возникает в цилиндрической оболочке открытого профиля при отношении 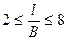, где В - ширина оболочки (рис. 10,1,а). Оболочки с указанным соотношением размеров относятся к оболочкам средней длины.

Из общих геометрических зависимостей (см. п. 5.7 раздела 5) следует выделить формулы:

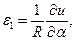(10.3,а)

ϰ 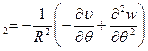(10.3,б)

и использовать их в качестве определений основных деформаций полоски*.

Осевые деформации полоски в окружном направлении и деформации сдвига полагают отсутствующими, т. е.

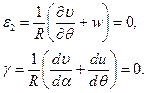(10.4,а)

В определениях деформаций по этим формулам, как и в условиях равновесия (10.1), введена безразмерная координата .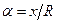

Физические соотношения могут быть получены по формулам (6.10) лекции № 6 в результате подстановки деформаций (10.3) и (10.4):

,

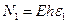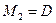ϰ, (10.5)

где величина «цилиндрической» жёсткости 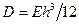вычисляется при 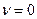(это значение коэффициента Пуассона обычно принимается при расчёте железобетонных оболочек).

10.2 Разрешающее уравнение полумоментной теории цилиндрической оболочки. Функция напряжений

Уравнения состояния цилиндрических оболочек можно привести к одному разрешающему уравнению, содержащему единственную неизвестную. Но сначала путём исключения из условий равновесия (10.1) усилий 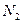, , 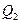, 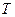а из (10.4,а) с помощью (10.4,б) - перемещений 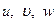, привлекая к тому же определения усилий по (10.5), после небольших преобразований можно установить два уравнения:

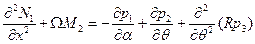, (10.6,а)

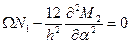. (10.6,б)

Здесь 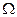- дифференциальный оператор (полумоментной теории) цилиндрической оболочки, структура которого имеет вид

;

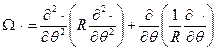под точкой после символа самого оператора и частной производной подразумевается одно из усилий - 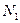, или .

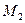Система однородных уравнений, полученных из (10.6) в результате приравнивания правой части первого уравнения системы нулю, при постоянной толщине оболочки может быть приведена к одному разрешающему уравнению путём введения функции усилий 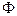согласно следующим определениям усилий:

,

,

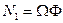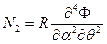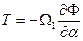, (10.7)

,

,

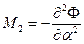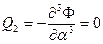где

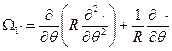
- ещё один, более короткий, дифференциальный оператор рассматриваемой оболочки.

Разрешающее уравнение имеет вид

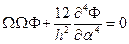. (10.8)

Принимая во внимание краевые условия конкретной задачи, выраженные через функцию 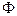, можно найти непосредственно функцию усилий .

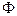В качестве частного решения всегда можно взять усилия безмоментного состояния: *.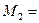

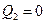10.3. Интегрирование основного уравнения полумоментной теории цилиндрической оболочки

Интеграл дифференциального уравнения четвёртого порядка

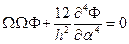
нетрудно установить, воспользовавшись решением известной задачи динамики стержня с непрерывным распределением массы. Как и там, неизвестную функцию 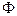необходимо представить в виде ряда, составленного из произведений двух функций, каждая из которых зависит только от какой-либо одной переменной рассматриваемой задачи, т.е. решение следует принять в виде**

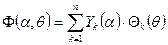. (10.9)

При этом одну группу функций, 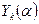, например, набирают среди балочных:

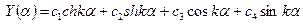, (10.10)

причём берут те из них, что отвечают конкретным условиям опирания торцов оболочки. Другая группа функций отыскивается из уравнения (10.8). В результате подстановки (10.9) в (10.8) составляют выражение

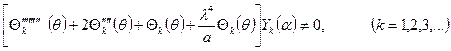. (10.11)

Неравенство нулю объясняется тем, что принятая согласно (10.9) функция 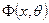удовлетворяет основному уравнению (10.8) благодаря выбору одной из составляющих её частей ( 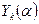) только на границах.

Чтобы максимально приблизить функцию 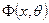к истинным значениям по всей длине оболочки, можно воспользоваться вариационным методом Бубнова – Галёркина. Для этого необходимо умножить выражение (10.11) на 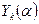, а затем проинтегрировать его в пределах от нуля до .

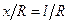Поскольку балочные функции обладают свойством ортогональности, т. е.

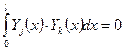при ,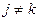

постольку правая часть уравнений

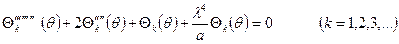(10.12)

в результате интегрирования будет нулевой. Таким образом, каждое уравнение второй группы искомой функции должно удовлетворять полученному обыкновенному дифференциальному уравнению восьмого порядка.

Последовательность решения такого рода уравнений хорошо известна. Определив корни характеристического уравнения

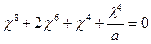
или

,

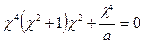каковыми в рассматриваемом случае являются величины

, (10.12)

где 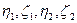зависят от 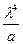, находят общее решение

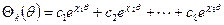. (10.13)

Если рассматривать область оболочки вдоль образующей вблизи края с положительной координатой ( 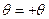), то в решении можно ограничиться четырьмя корнями с положительными вещественными частями:

. (10.14)

Соответствующее решение имеет вид

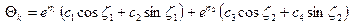. (10.15)

Т. к. слагаемые содержат произвольные постоянные, то ничего не изменится, если первое из них умножить на 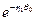, а второе – на 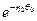. Воспользовавшись новой координатой для отсчёта углов, начинающихся от края 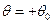, в виде

,

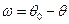функцию 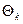можно представить в более удобной форме

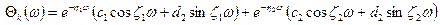. (10.17)

В конечном счёте общее решение основного уравнения принимает вид

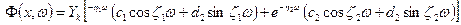. (10.18)

На его основе с помощью формул (10.7) усилия в оболочке можно выразить через функции, которые входят в (10.18). Кроме того, перемещения также могут быть выражены через них. Это позволит без затруднений составить краевые условия и на их основе найти постоянные интегрирования.

Замечания:

1. Корни характеристического уравнения могут быть записаны в общем виде

.

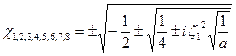Анализ величин, входящих в данное выражение, для оболочек средней длины указывает на то, что слагаемые практически не оказывают влияния на величину корней и потому могут быть опущены. Следовательно, корни можно вычислять по формуле

,

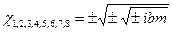где

;

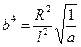в таком случае

,

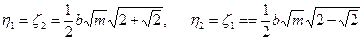т. е. все корни зависят лишь от одного параметра оболочки .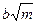

1. Обоснование выражений для усилий согласно (10.7) будет дано в следующем разделе, в котором рассматривается общая (моментная) теория расчёта цилиндрических оболочек.

10.4. Приближённые методы анализа напряжённого состояния цилиндрической оболочки

Очевидно, выполнение расчётов цилиндрических оболочек путём интегрирования уравнений, встречает затруднения. Поэтому рядом учёных были предложены другие подходы. В частности, Власов В. З. развил теорию «заменяющей складки», когда анализ оболочки сводится к расчёту складчатой системы. При этом применяются классические методы строительной механики – метод сил или метод перемещений. Обширные исследования состояния цилиндрических оболочек проведены в работах отечественных учёных: Пастернак П.Л. [19] воспользовался методом сил, Милейковский И. Е. [11] - методом перемещений. Другое направление исследований в работах Лауля Х. Х., Канна С. Н. основано на «балочной» теории [19].

* Формула для кривизны полоски, согласно (10.3,б), совпадает с формулой, определяющей кривизну арки [11].

* U. Fisterwalder в 1932 году предложил известную конструкцию перекрытий системы «Zeiss - Dywidag», в основе которой лежит теория рассматриваемой оболочки без учёта кинематической предпосылки (10.4,а).

** Решение дифференциального уравнения (10.8) в виде (10.9) предложено Канторовичем [9].