Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 14 страница
Взаимосвязь между двойственными корпускулярно-волновыми свойствами света можно объяснить, если использовать, как это делает квантовая оптика, статистический подход к рассмотрению закономерностей распространения света. Например, дифракция света на щели состоит в том, что при прохождении света через щель происходит перераспределение фотонов в пространстве. Так как вероятность попадания фотонов в различные точки экрана неодинакова, то и возникает дифракционная картина. Освещенность экрана пропорциональна вероятности попадания фотонов на единицу площади экрана. С другой стороны, по волновой теории, освещенность пропорциональна квадрату амплитуды световой волны в той же точке экрана. Следовательно, квадрат амплитуды световой волны в данной точке пространства является мерой вероятности попадания фотонов в данную точку.
6 ЭЛЕМЕНТЫ КВАНТОВОЙ ФИЗИКИ АТОМОВ, МОЛЕКУЛ И ТВЕРДЫХ ТЕЛ
Глава 27 Теория атома водорода по Бору
§ 208. Модели атома Томсона и Резерфорда
Представление об атомах как неделимых мельчайших частицах вещества («атомос» — неразложимый) возникло еще в античные времена (Демокрит, Эпикур, Лукреций). В средние века, во времена безграничного господства церкви, учение об атомах, будучи материалистическим, естественно, не могло получить признания, а тем более дальнейшего развития. К началу XVIII в. атомистическая теория приобретает все большую популярность, так как к этому времени в работах А. Лавуазье (1743—1794, французский химик), М. В. Ломоносова и Д. Дальтона была доказана реальность существования атомов. Однако в это время вопрос о внутреннем строении атомов даже не возникал, так как атомы по-прежнему считались неделимыми.
Большую роль в развитии атомистической теории сыграл Д. И. Менделеев, разработавший в 1869 г. Периодическую систему элементов, в которой впервые на научной основе был поставлен вопрос о единой природе атомов. Во второй половине XIX в. экспериментально было доказано, что электрон является одной из основных составных частей любого вещества. Эти выводы, а также многочисленные экспериментальные данные привели к тому, что в начале XX в. серьезно встал вопрос о строении атома.
Первая попытка создания на основе накопленных экспериментальных данных модели атома принадлежит Дж. Дж. Томсону (1903). Согласно этой модели, атом представляет собой непрерывно заряженный положительным зарядом шар радиусом порядка 10–10 м, внутри которого около своих положений равновесия колеблются электроны; суммарный отрицательный заряд электронов равен положительному заряду шара, поэтому атом в целом нейтрален. Через несколько лет было доказано, что представление о непрерывно распределенном внутри атома положительном заряде ошибочно.
В развитии представлений о строении атома велико значение опытов английского физика Э. Резерфорда (1871—1937) по рассеянию a-частиц в веществе. Альфа-частицы возникают при радиоактивных превращениях; они являются положительно заряженными частицами с зарядом 2е и массой, примерно в 7300 раз большей массы электрона. Пучки a-частиц обладают высокой монохроматичностью (для данного превращения имеют практически одну и ту же скорость (порядка 107 м/с)).
Резерфорд, исследуя прохождение a-частиц в веществе (через золотую фольгу толщиной примерно 1 мкм), показал, что основная их часть испытывает незначительные отклонения, но некоторые a-частицы (примерно одна из 20 000) резко отклоняются от первоначального направления (углы отклонения достигали даже 180°). Так как электроны не могут существенно изменить движение столь тяжелых и быстрых частиц, как a-частицы, то Резерфордом был сделан вывод, что значительное отклонение a-частиц обусловлено их взаимодействием с положительным зарядом большой массы. Однако значительное отклонение испытывают лишь немногие a-частицы; следовательно, лишь некоторые из них проходят вблизи данного положительного заряда. Это, в свою очередь, означает, что положительный заряд атома сосредоточен в объеме, очень малом по сравнению с объемом атома.
На основании своих исследований Резерфорд в 1911 г. предложил ядерную (планетарную) модель атома. Согласно этой модели, вокруг положительного ядра, имеющего заряд Zе (Z — порядковый номер элемента в системе Менделеева, е — элементарный заряд), размер 10–15—10–14 м и массу, практически равную массе атома, в области с линейными размерами порядка 10–10 м по замкнутым орбитам движутся электроны, образуя электронную оболочку атома. Так как атомы нейтральны, то заряд ядра равен суммарному заряду электронов, т. е. вокруг ядра должно вращаться Z электронов.
Для простоты предположим, что электрон движется вокруг ядра по круговой орбите радиуса r. При этом кулоновская сила взаимодействия между ядром и электроном сообщает электрону центростремительное ускорение. Второй закон Ньютона для электрона, движущегося по окружности под действием кулоновской силы, имеет вид
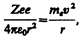 (208.1)
(208.1)
где тe, и v — масса и скорость электрона на орбите радиуса r, e0 — электрическая постоянная.
Уравнение (208.1) содержит два неизвестных: r и v. Следовательно, существует бесчисленное множество значений радиуса и соответствующих ему значений скорости (а значит, и энергии), удовлетворяющих этому уравнению. Поэтому величины r, v (следовательно, и Е) могут меняться непрерывно, т. е. может испускаться любая, а не вполне определенная порция энергии. Тогда спектры атомов должны быть сплошными. В действительности же опыт показывает, что атомы имеют линейчатый спектр. Из выражения (208.1) следует, что при r»10–10 м скорость движения электронов v = 106 м/с, а ускорение v2/r =1022 м/с2. Согласно классической электродинамике, ускоренно движущиеся электроны должны излучать электромагнитные волны и вследствие этого непрерывно терять энергию. В результате электроны будут приближаться к ядру и в конце концов упадут на него. Таким образом, атом Резерфорда оказывается неустойчивой системой, что опять-таки противоречит действительности.
Попытки построить модель атома в рамках классической физики не привели к успеху: модель Томсона была опровергнута опытами Резерфорда, ядерная же модель оказалась неустойчивой электродинамически и противоречила опытным данным. Преодоление возникших трудностей потребовало создания качественно новой — квантовой — теории атома.
§ 209. Линейчатый спектр атома водорода
Исследования спектров излучения разреженных газов (т. е. спектров излучения отдельных атомов) показали, что каждому газу присущ определенный линейчатый спектр, состоящий из отдельных спектральных линий или групп близко расположенных линий. Самым изученным является спектр наиболее простого атома — атома водорода.
Швейцарский ученый И. Бальмер (1825—1898) подобрал эмпирическую формулу, описывающую все известные в то время спектральные линии атома водорода в видимой области спектра:
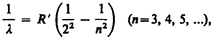 (209.1)
(209.1)
где R'=1,10×107 м–1 — постоянная Ридберга.* Taк как n = c/l, то формула (209.1) может быть переписана для частот:
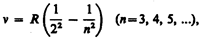 (209.2)
(209.2)
где R=R'c=3,29×1015 с–1 — также постоянная Ридберга.
* И. Ридберг (1854—1919) — шведский ученый, специалист в области спектроскопии.
Из выражений (209.1) и (209.2) вытекает, что спектральные линии, отличающиеся различными значениями п, образуют группу или серию линий, называемую серией Бальмера. С увеличением n линии серии сближаются; значение n = ¥ определяет границу серии, к которой со стороны больших частот примыкает сплошной спектр.
В дальнейшем (в начале XX в.) в спектре атома водорода было обнаружено еще несколько серий. В ультрафиолетовой области спектра находится серия Лаймана:
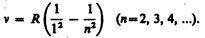
В инфракрасной области спектра были также обнаружены:
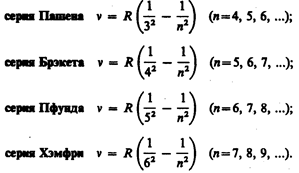
Все приведенные выше серии в спектре атома водорода могут быть описаны одной формулой, называемой обобщенном формулой Бальмера:
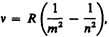 (209.3)
(209.3)
где т имеет в каждой данной серии постоянное значение, m = 1, 2, 3, 4, 5, 6 (определяет серию), п принимает целочисленные значения начиная с т+1 (определяет отдельные линии этой серии).
Исследование более сложных спектров — спектров паров щелочных металлов (например, Li, Na, К) — показало, что они представляются набором незакономерно расположенных линий. Ридбергу удалось разделить их на три серии, каждая из которых располагается подобно линиям бальмеровской серии.
Приведенные выше сериальные формулы подобраны эмпирически и долгое время не имели теоретического обоснования, хотя и были подтверждены экспериментально с очень большой точностью. Приведенный выше вид сериальных формул, удивительная повторяемость в них целых чисел, универсальность постоянной Ридберга свидетельствуют о глубоком физическом смысле найденных закономерностей, вскрыть который в рамках классической физики оказалось невозможным.
§ 210. Постулаты Бора
Первая попытка построить качественно новую — квантовую — теорию атома была предпринята в 1913 г. датским физиком Нильсом Бором (1885—1962). Он поставил перед собой цель связать в единое целое эмпирические закономерности линейчатых спектров, ядерную модель атома Резерфорда и квантовый характер излучения и поглощения света. В основу своей теории Бор положил два постулата.
Первый постулат Бора (постулат стационарных состояний):в атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергии. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Движение электронов по стационарным орбитам не сопровождается излучением электромагнитных волн.
В стационарном состоянии атома электрон, двигаясь по круговой орбите, должен иметь дискретные квантованные значения момента импульса, удовлетворяющие условию
 (210.1)
(210.1)
где те — масса электрона, v — его скорость по n-й орбите радиуса rn, ћ = h/(2p).
Втором постулат Бора (правило частот):при переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией
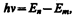 (210.2)
(210.2)
равной разности энергий соответствующих стационарных состояний (Еn и Em — соответственно энергии стационарных состояний атома до и после излучения (поглощения)). При Еm<Еn происходит излучение фотона (переход атома из состояния с большей энергией в состояние с меньшей энергией, т. е. переход электрона с более удаленной от ядра орбиты на более близлежащую), при Еm>Еn — его поглощение (переход атома в состояние с большей энергией, т. е. переход электрона на более удаленную от ядра орбиту). Набор возможных дискретных частот n = (En—Em)/h квантовых переходов и определяет линейчатый спектр атома.
§ 211. Опыты Франка и Герца
Изучая методом задерживающего потенциала столкновения электронов с атомами газов (1913), Д. Франк и Г. Герц экспериментально доказали дискретность значений энергии атомов. Принципиальная схема их установки приведена на рис. 292. Вакуумная трубка, заполненная парами ртути (давление приблизительно равно 13 Па), содержала катод (К), две сетки (C1 и С2) и анод (А). Электроны, эмиттируемые катодом, ускорялись разностью потенциалов, приложенной между катодом и сеткой C1. Между сеткой С2 и анодом приложен небольшой (примерно 0,5 В) задерживающий потенциал.

Электроны, ускоренные в области 1, попадают в область 2 между сетками, где испытывают соударения с атомами паров ртути. Электроны, которые после соударений имеют достаточную энергию для преодоления задерживающего потенциала в области 3, достигают анода. При неупругих соударениях электронов с атомами ртути последние могут возбуждаться. Согласно боровской теории, каждый из атомов ртути может получить лишь вполне определенную энергию, переходя при этом в одно из возбужденных состояний. Поэтому если в атомах действительно существуют стационарные состояния, то электроны, сталкиваясь с атомами ртути, должны терять энергию дискретно, определенными порциями, равными разности энергий соответствующих стационарных состояний атома.
Из опыта следует (рис. 293), что при увеличении ускоряющего потенциала вплоть до 4,86 В анодный ток возрастает монотонно, его значение проходит через максимум (4,86 В), затем резко уменьшается и возрастает вновь. Дальнейшие максимумы наблюдаются при 2×4,86 и 3×4,86 В.
Ближайшим к основному, невозбужденному, состоянию атома ртути является возбужденное состояние, отстоящее от основного по шкале энергий на 4,86 эВ. Пока разность потенциалов между катодом и сеткой меньше 4,86 В, электроны, встречая на своем пути атомы ртути, испытывают с ними только упругие соударения. При еj = 4,86 эВ энергия электрона становится достаточной, чтобы вызвать неупругий удар, при котором электрон отдает атому ртути всю кинетическую энергию, возбуждая переход одного из электронов атома из нормального энергетического состояния на возбужденный энергетический уровень. Электроны, потерявшие свою кинетическую энергию, уже не смогут преодолеть тормозящего поля и достигнуть анода. Этим и объясняется первое резкое падание анодного тока при еj = 4,86 эВ. При значениях энергии, кратных 4,86 эВ, электроны могут испытать с атомами ртути 2, 3, ... неупругих соударения, потеряв при этом полностью свою энергию, и не достигнуть анода, т. е. должно наблюдаться резкое падение анодного тока. Это действительно наблюдается на опыте (рис. 293).
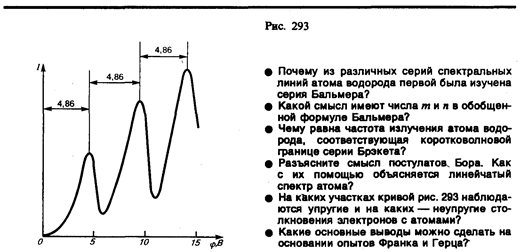
Таким образом, опыты Франка и Герца показали, что электроны при столкновении с атомами ртути передают атомам только определенные порции энергии, причем 4,86 эВ — наименьшая возможная порция энергии (наименьший квант энергии), которая может быть поглощена атомом ртути в основном энергетическом состоянии. Следовательно, идея Бора о существовании в атомах стационарных состояний блестяще выдержала экспериментальную проверку.
Атомы ртути, получившие при соударении с электронами энергию DE, переходят в возбужденное состояние и должны возвратиться в основное, излучая при этом, согласно второму постулату Бора (см. (210.2)), световой квант с частотой n = DE/h. По известному значению DE = 4,86 эВ можно вычислить длину волны излучения: l= hc/DE » 255 нм. Таким образом, если теория верна, то атомы ртути, бомбардируемые электронами с энергией 4,86 эВ, должны являться источником ультрафиолетового излучения с l » 255 нм. Опыт действительно обнаруживает одну ультрафиолетовую линию с l » 254 нм. Таким образом, опыты Франка и Герца экспериментально подтвердили не только первый, но и второй постулат Бора. Эти опыты сыграли огромное значение в развитии атомной физики.
§ 212. Спектр атома водорода по Бору
Постулаты, выдвинутые Бором, позволили рассчитать спектр атома водорода и водородоподобных систем — систем, состоящих из ядра с зарядом Ze и одного электрона (например, ионы Не+, Li2+), а также теоретически вычислить постоянную Ридберга.
Следуя Бору, рассмотрим движение электрона в водородоподобной системе, ограничиваясь круговыми стационарными орбитами. Решая совместно уравнение (208.1) 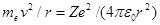 , предложенное Резерфордом, и уравнение (210.1), получим выражение для радиуса n-й стационарной орбиты:
, предложенное Резерфордом, и уравнение (210.1), получим выражение для радиуса n-й стационарной орбиты:
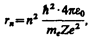 (212.1)
(212.1)
где n = 1, 2, 3, ... . Из выражения (212.1) следует, что радиусы орбит растут пропорционально квадратам целых чисел.
Для атома водорода (Z = 1) радиус первой орбиты электрона при n = 1, называемый первым боровоским радиусом (а), равен
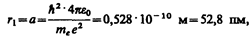 (212.2)
(212.2)
что соответствует расчетам на основании кинетической теории газов. Так как радиусы стационарных орбит измерить невозможно, то для проверки теории необходимо обратиться к таким величинам, которые могут быть измерены экспериментально. Такой величиной является энергия, излучаемая и поглощаемая атомами водорода.
Полная энергия электрона в водородоподобной системе складывается из его кинетической энергии (тev2/2) и потенциальной энергии в электростатическом поле ядра (–Ze2/(4pe0r)):
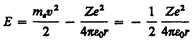
(учли, что 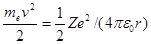 ; см. (208.1)). Учитывая квантованные для радиуса n-й стационарной орбиты значения (212.1), получим, что энергия электрона может принимать только следующие дозволенные дискретные значения:
; см. (208.1)). Учитывая квантованные для радиуса n-й стационарной орбиты значения (212.1), получим, что энергия электрона может принимать только следующие дозволенные дискретные значения:
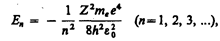 (212.3)
(212.3)
где знак минус означает, что электрон находится в связанном состоянии.
Из формулы (212.3) следует, что энергетические состояния атома образуют последовательность энергетических уровней, изменяющихся в зависимости от значения n. Целое число n в выражении (212.3), определяющее энергетические уровни атома, называется главным квантовым числом. Энергетическое состояние с n=1 является основным (нормальным) состоянием; состояния с n > 1 являются возбужденными. Энергетический уровень, соответствующий основному состоянию атома, называется основным (нормальным) уровнем; все остальные уровни являются возбужденными.
Придавая n различные целочисленные значения, получим для атома водорода (Z = 1), согласно формуле (212.3), возможные уровни энергии, схематически представленные на рис. 294. Энергия атома водорода с увеличением n возрастает и энергетические уровни сближаются к границе, соответствующей значению n = ¥. Атом водорода обладает, таким образом, минимальной энергией (E1 = –13,55 эВ) при n = 1 и максимальной (Е¥ = 0) при n = ¥. Следовательно, значение Е¥ = 0 соответствуетионизацииатома (отрыву от него электрона). Согласно второму постулату Бора (см. (210.2)), при переходе атома водорода (Z= 1) из стационарного состояния л в стационарное состояние т с меньшей энергией испускается квант
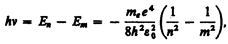
откуда частота излучения
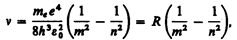 (212.4)
(212.4)
где R = mee4/(8h3 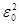 ).
).
Воспользовавшись при вычислении R современными значениями универсальных постоянных, получим величину, совпадающую с экспериментальным значением постоянной Ридберга в эмпирических формулах для атома водорода (см. § 209). Это совпадение убедительно доказывает правильность полученной Бором формулы (212.3) для энергетических уровней водородоподобной системы.
Подставляя, например, в формулу (212.4) т=1 и п=2, 3, 4, ..., получим группу линий, образующих серию Лаймана (см. § 209) и соответствующих переходам электронов с возбужденных уровней (n = 2, 3, 4, ...) на основной (m = l). Аналогично, при подстановке m = 2, 3, 4, 5, 6 и соответствующих им значений n получим серии Бальмера, Пашена, Брэкета, Пфунда и Хэмфри (часть из них схематически представлена на рис. 294), описанные в § 209. Следовательно, по теории Бора, количественно объяснившей спектр атома водорода, спектральные серии соответствуют излучению, возникающему в результате перехода атома в данное состояние из возбужденных состояний, расположенных выше данного.
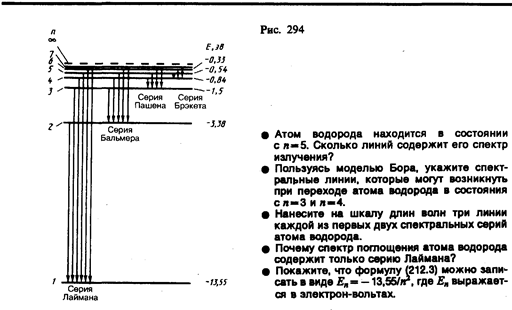
Спектр поглощения атома водорода является линейчатым, но содержит при нормальных условиях только серию Лаймана. Он также объясняется теорией Бора. Так как свободные атомы водорода обычно находятся в основном состоянии (стационарное состояние с наименьшей энергией при n = 1), то при сообщении атомам извне определенной энергии могут наблюдаться лишь переходы атомов из основного состояния в возбужденные (возникает серия Лаймана).
Теория Бора была крупным шагом в развитии атомной физики и явилась важным этапом в создании квантовой механики. Однако эта теория обладает внутренними противоречиями (с одной стороны, применяет законы классической физики, а с другой — основывается на квантовых постулатах). В теории Бора рассмотрены спектры атома водорода и водородоподобных систем и вычислены частоты спектральных линий, однако эта теория не смогла объяснить интенсивности спектральных линий и ответить на вопрос: почему совершаются те или иные переходы? Серьезным недостатком теории Бора была невозможность описания с ее помощью спектра атома гелия — одного из простейших атомов, непосредственно следующего за атомом водорода.
Глава 28 Элементы квантовой механики
§ 213. Корпускулярно-волновой дуализм свойств вещества
Французский ученый Луи де Бройль (1892—1987), осознавая существующую в природе симметрию и развивая представления о двойственной корпускулярно-волновой природе света, выдвинул в 1923 г. гипотезу об универсальности корпускулярно-волнового дуализма. Де Бройль утверждал, что не только фотоны, но и электроны и любые другие частицы материи наряду с корпускулярными обладают также волновыми свойствами.
Итак, согласно де Бройлю, с каждым микрообъектом связываются, с одной стороны, корпускулярные характеристики — энергия Е и импульс p, а с другой — волновые характеристики — частота n и длина волны l. Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов:
 (213.1)
(213.1)
Смелость гипотезы де Бройля заключалась именно в том, что соотношение (213.1) постулировалось не только для фотонов, но и для других микрочастиц, в частности для таких, которые обладают массой покоя. Таким образом, любой частице, обладающей импульсом, сопоставляют волновой процесс с длиной волны, определяемойпо формуле де Бройля:
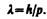 (213.2)
(213.2)
Это соотношение справедливо для любой частицы с импульсом р.
Вскоре гипотеза де Бройля была подтверждена экспериментально. В 1927 г. американские физики К. Дэвиссон (1881—1958) и Л. Джермер (1896—1971) обнаружили, что пучок электронов, рассеивающийся от естественной дифракционной решетки — кристалла никеля, — дает отчетливую дифракционную картину. Дифракционные максимумы соответствовали формуле Вульфа — Брэггов (182.1), а брэгговская длина волны оказалась в точности равной длине волны, вычисленной по формуле (213.2). В дальнейшем формула де Бройля была подтверждена опытами П. С. Тартаковского и Г. Томсона, наблюдавших дифракционную картину при прохождении пучка быстрых электронов (энергия »50 кэВ) через металлическую фольгу (толщиной »1 мкм).
Так как дифракционная картина исследовалась для потока электронов, то необходимо было доказать, что волновые свойства присущи не только потоку большой совокупности электронов, но и каждому электрону в отдельности. Это удалось экспериментально подтвердить в 1948 г. российскому физику В. А. Фабриканту (р. 1907). Он показал, что даже в случае столь слабого электронного пучка, когда каждый электрон проходит через прибор независимо от других (промежуток времени между двумя электронами в 104 раз больше времени прохождения электроном прибора), возникающая при длительной экспозиции дифракционная картина не отличается от дифракционных картин, получаемых при короткой экспозиции для потоков электронов, в десятки миллионов раз более интенсивных. Следовательно, волновые свойства частиц не являются свойством их коллектива, а присущи каждой частице в отдельности.
Впоследствии дифракционные явления обнаружили также для нейтронов, протонов, атомных и молекулярных пучков. Это окончательно послужило доказательством наличия волновых свойств микрочастиц и позволило описывать движение микрочастиц в виде волнового процесса, характеризующегося определенной длиной волны, рассчитываемой по формуле де Бройля (213.2). Открытие волновых свойств микрочастиц привело к появлению и развитию новых методов исследования структуры веществ, таких,как электронография и нейтронография (см. § 182), а также к возникновению новой отрасли науки — электронной оптики (см. § 169).
Экспериментальное доказательство наличия волновых свойств микрочастиц привело к выводу о том, что перед нами универсальное явление, общее свойство материи. Но тогда волновые свойства должны быть присущи и макроскопическим телам. Почему же они не обнаружены экспериментально? Например, частице массой 1 г, движущейся со скоростью 1 м/с, соответствует волна де Бройля с l = 6,62×10–31 м. Такая длина волны лежит за пределами доступной наблюдению области (периодических структур с периодом d»10–31 м не существует). Поэтому считается, что макроскопические тела проявляют только одну сторону своих свойств — корпускулярную — и не проявляют волновую.
Представление о двойственной корпускулярно-волновой природе частиц вещества углубляется еще тем, что на частицы вещества переносится связь между полной энергией частицы e и частотой n волн де Бройля:
 (213.3)
(213.3)
Это свидетельствует о том, что соотношение между энергией и частотой в формуле (213.3) имеет характер универсального соотношения, справедливогокак для фотонов, так и для любых других микрочастиц. Справедливость же соотношения (213.3) вытекает из согласия с опытом тех теоретических результатов, которые получены с его помощью в квантовой механике, атомной и ядерной физике.
Подтвержденная экспериментально гипотеза да Бройля о корпускулярно-волновом дуализме свойств вещества коренным образом изменила представления о свойствах микрообъектов. Всем микрообъектам присущи и корпускулярные, и волновые свойства; в то же время любую из микрочастиц нельзя считать ни частицей, ни волной в классическом понимании. Современная трактовка корпускулярно-волнового дуализма может быть выражена словами академика В. А. Фока (1898—1974): «Можно сказать, что для атомного объекта существует потенциальная возможность проявлять себя, в зависимости от внешних условий, либо как волна, либо как частица, либо промежуточным образом. Именно в этой потенциальной возможности различных проявлений свойств, присущих микрообъекту, и состоит дуализм волна—частица. Всякое иное, более буквальное, понимание этого дуализма в вида какой-нибудь модели неправильно.» (в сб.: Философские вопросы современной физики. — М.: Изд-во АН СССР, 1959).
§ 214. Некоторые свойства волн да Бройля
Рассмотрим свободно движущуюся со скоростью v частицу массой т. Вычислим для нее фазовую и групповую скорости волн да Бройля. Фазовая скорость, согласно (154.8),
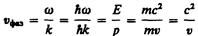 (214.1)
(214.1)
(E=ћw и p=ћk, где k=2p/l—волновое число). Так как c>v, то фазовая скорость волн де Бройля больше скорости света в вакууме (фазовая скорость волн может быть как меньше, так и больше с в отличие от групповой скорости волн (см. § 155)). Групповая скорость, согласно (155.1),
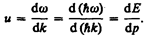
Для свободной частицы 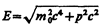 (см. (40.7)) и
(см. (40.7)) и
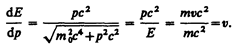
Следовательно, групповая скорость волн де Бройля равна скорости частицы.
Групповая скорость фотона 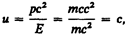 т. е. равна скорости самого фотона.
т. е. равна скорости самого фотона.
Дата добавления: 2015-12-16; просмотров: 555;
