Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 8 страница
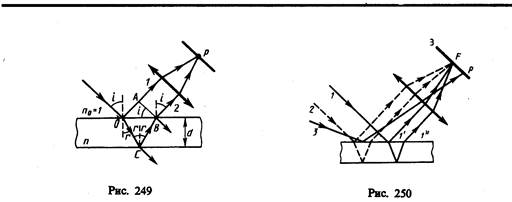
2. Полосы равной толщины (интерференция от пластинки переменной толщины).Пусть на клин (угол a между боковыми гранями мал) падает плоская волна, направление распространения которой совпадает с параллельными лучами 1 и 2 (рис. 251). Из всех лучей, на которые разделяется падающий луч 1, рассмотрим лучи 1' и 1", отразившиеся от верхней и нижней поверхностей клина. При определенном взаимном положении клина и линзы лучи 1' и 1" пересекутся в некоторой точке А, являющейся изображением точки В. Так как лучи 1' и 1" когерентны, они будут интерферировать. Если источник расположен довольно далеко от поверхности клина и угол a ничтожно мал, то оптическая разность хода между интерферирующими лучами 1' и 1" может быть с достаточной степенью точности вычислена по формуле (174.1), где d — толщина клина в месте падения на него луча. Лучи 2' и 2", образовавшиеся при делении луча 2, падающего в другую точку клина, собираются линзой в точке А'. Оптическая разность хода уже определяется толщиной d'. Таким образом, на экране возникает система интерференционных полос. Каждая из полос возникает при отражении от мест пластинки, имеющих одинаковую толщину (в общем случае толщина пластинки может изменяться произвольно). Интерференционные полосы, возникающие в результате интерференции от мест одинаковой толщины, называются полосами равной толщины.
Так как верхняя и нижняя грани клина не параллельны между собой, то лучи 1' и 1" (2' и 2") пересекаются вблизи пластинки, в изображенном на рис. 251 случае — над ней (при другой конфигурации клина они могут пересекаться и под пластинкой). Таким образом, полосы равной толщины локализованы вблизи поверхности клина. Если свет падает на пластинку нормально, то полосы равной толщины локализуются на верхней поверхности клина.
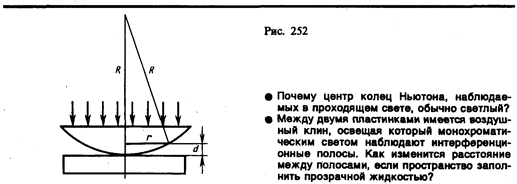
3. Кольца Ньютона. Кольца Ньютона, являющиеся классическим примером полос равной толщины, наблюдаются при отражении света от воздушного зазора, образованного плоскопараллельной пластинкой и соприкасающейся с ней плосковыпуклой линзой с большим радиусом кривизны (рис. 252). Параллельный пучок света падает нормально на плоскую поверхность линзы и частично отражается от верхней и нижней поверхностей воздушного зазора между линзой и пластинкой. При наложении отраженных лучей возникают полосы равной толщины, при нормальном падения света имеющие вид концентрических окружностей.
В отраженном свете оптическая разность хода (с учетом потери полуволны при отражении), согласно (174.1), при условии, что показатель преломления воздуха n=1, а i=0,
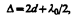
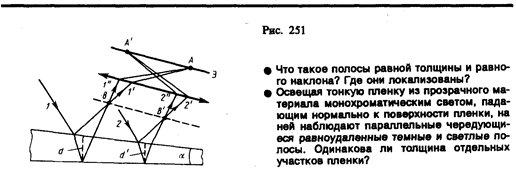
где d—ширина зазора. Из рис. 252 следует, что 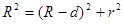 , где R—радиус кривизны линзы, r — радиус кривизны окружности, всем точкам которой соответствует одинаковый зазор d. Учитывая, что d мало, получим d=r2/(2R). Следовательно,
, где R—радиус кривизны линзы, r — радиус кривизны окружности, всем точкам которой соответствует одинаковый зазор d. Учитывая, что d мало, получим d=r2/(2R). Следовательно,
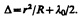 (174.4)
(174.4)
Приравняв (174.4) к условиям максимума (172.2) и минимума (172.3), получим выражения для радиусов m-го светлого кольца и m-го темного кольца соответственно
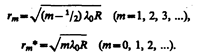
Измеряя радиусы соответствующих колец, можно (зная радиус кривизны линзы R) определить l0 и, наоборот, по известной l0 найти радиус кривизны R линзы.
Как для полос равного наклона, так и для полос равной толщины положение максимумов зависит от длины волны l0 (см. (174.2)). Поэтому система светлых и темных полос получается только при освещении монохроматическим светом. При наблюдении в белом свете получается совокупность смещенных друг относительно друга полос, образованных лучами разных длин волн, и интерференционная картина приобретает радужную окраску. Все рассуждения были проведены для отраженного света. Интерференцию можно наблюдать и в проходящем свете, причем в данном случае не наблюдается потери полуволны. Следовательно, оптическая разность хода для проходящего и отраженного света отличается на l0/2, т.е. максимумам интерференции в отраженном свете соответствуют минимумы в проходящем, и наоборот.
§ 175. Применение интерференции света
Явление интерференции обусловлено волновой природой света; его количественные закономерности зависят от длины волны l0. Поэтому это явление применяется для подтверждения волновой природы света и для измерения длин волн(интерференционная спектроскопия).
Явление интерференции применяется также для улучшения качества оптических приборов (просветление оптики) и получения высокоотражающих покрытий. Прохождение света через каждую преломляющую поверхность линзы, например через границу стекло–воздух, сопровождается отражением »4% падающего потока (при показателе преломления стекла »1,5). Так как современные объективы содержат большое количество линз, то число отражений в них велико, а поэтому велики и потери светового потока. Таким образом, интенсивность прошедшего света ослабляется и светосила оптического прибора уменьшается. Кроме того, отражения от поверхностей линз приводят к возникновению бликов, что часто (например, в военной технике) демаскирует положение прибора.
Для устранения указанных недостатков осуществляют так называемое просветление оптики. Для этого на свободные поверхности линз наносят тонкие пленки с показателем преломления, меньшим, чем у материала линзы. При отражении света от границ раздела воздух–пленка и пленка–стекло возникает интерференция когерентных лучей 1' и 2' (рис. 253). Толщину пленки d и показатели преломления стекла nс и пленки n можно подобрать так, чтобы волны, отраженные от обеих поверхностей пленки, гасили друг друга. Для этого их амплитуды должны быть равны, а оптическая разность хода равна 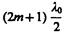 (см. (172.3)). Расчет показывает, что амплитуды отраженных лучей равны, если
(см. (172.3)). Расчет показывает, что амплитуды отраженных лучей равны, если
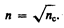 (175.1)
(175.1)
Так как nс, n и показатель преломления воздуха n0 удовлетворяют условиям nс >n>n0, то потеря полуволны происходит на обеих поверхностях; следовательно, условие минимума (предполагаем, что свет падает нормально, т. е. i=0)
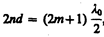
где nd —оптическая толщина пленки. Обычно принимают m=0, тогда
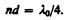
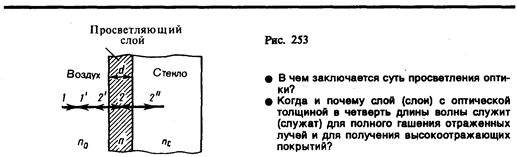
Таким образом, если выполняется условие (175.1) и оптическая толщина плевки равна l0/4, то в результате интерференции наблюдается гашение отраженных лучей. Taк как добиться одновременного гашения для всех длин воли невозможно, то это обычно делается для наиболее восприимчивой глазом длины волны l0»0,55 мкм. Поэтому объективы с просветленной оптикой имеют синевато-красный оттенок.
Создание высокоотражающих покрытий стало возможным лишь на основемноголучевой интерференции. В отличие от двухлучевой интерференции, которую мы рассматривали до сих пор, многолучевая интерференция возникает при наложении большого числа когерентных световых пучков. Распределение интенсивности в интерференционной картине существенно различается; интерференционные максимумы значительно уже и ярче,чем при наложении двух когерентных световых пучков. Так, результирующая амплитуда световых колебаний одинаковой амплитуды в максимумах интенсивности, где сложение происходит в одинаковой фазе, в N раз больше, а интенсивность в N2 раз больше, чем от одного пучка (N — число интерферирующих пучков). Отметим, что для нахождения результирующей амплитуды удобно пользоваться графическим методом, используя метод вращающегося вектора амплитуды (см. § 140). Многолучевая интерференция осуществляется в дифракционной решетке (см. § 180).
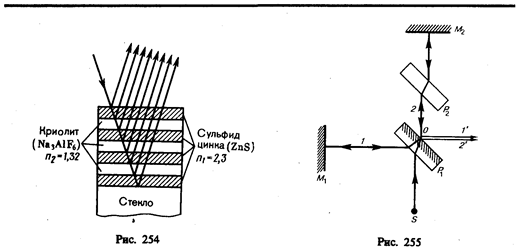
Многолучевую интерференцию можно осуществить в многослойной системе чередующихся пленок с разными показателями преломления (но одинаковой оптической толщиной, равной l0/4), нанесенных на отражающую поверхность (рис. 254). Можно показать, что на границе раздела пленок (между двумя слоями ZnS с большим показателем преломления п1 находится пленка криолита с меньшим показателем преломления n2) возникает большое число отраженных интерферирующих лучей, которые при оптической толщине пленок l0/4 будут взаимно усиливаться, т. е. коэффициент отражения возрастает. Характерной особенностью такой высокоотражательной системы является то, что она действует в очень узкой спектральной области, причем чем больше коэффициент отражения, тем уже эта область. Например, системаиз семипленок для области 0,5мкм дает коэффициент отражения r»96% (при коэффициенте пропускания »3,5% и коэффициенте поглощения <0,5%). Подобные отражатели применяются в лазерной технике, а также используются для создания интерференционных светофильтров (узкополосных оптических фильтров).
Явление интерференции также применяется в очень точных измерительных приборах, называемых интерферометрами. Все интерферометры основаны на одном и том же принципе и различаются лишь конструкционно. На рис. 255 представлена упрощенная схема интерферометра Майкельсона. Монохроматический свет от источника S падает под углом 45° на плоскопараллельную пластинку P1. Сторона пластинки, удаленная от S, посеребренная и полупрозрачная, разделяет луч на две части: луч 1 (отражается от посеребренного слоя) в луч 2 (проходит через него). Луч 1 отражается от зеркала M1 и, возвращаясь обратно, вновь проходит через пластинку P1 (луч 1'). Луч 2 идет к зеркалу М2, отражается от него, возвращается обратно и отражается от пластинки Р1 (луч 2'). Так как первый из лучей проходит сквозь пластинку Р1 дважды, то для компенсации возникающей разности хода на пути второго луча ставится пластинка Р2 (точно такая же, как и Р1, только не покрытая слоем серебра).
Лучи 1' и 2' когерентны; следовательно, будет наблюдаться интерференция, результат которой зависит от оптической разности хода луча 1 от точки О до зеркала М1 и луча 2 от точки О до зеркала M2. При перемещении одного из зеркал на расстояние l0/4 разность хода обоих лучей увеличится на l0/2 и произойдет смена освещенности зрительного поля. Следовательно, по незначительному смещению интерференционной картины можно судить о малом перемещении одного из зеркал и использовать интерферометр Майкельсона для точного (порядка 10–7 м) измерения длин (измерения длины тел, длины волны света, изменения длины тела при изменении температуры (интерференционный дилатометр)).
Российский физик В. П. Линник (1889—1984) использовал принцип действия интерферометра Майкельсона для создания микроинтерферометра (комбинация интерферометра и микроскопа), служащего для контроля чистоты обработки поверхности.
Интерферометры — очень чувствительные оптические приборы, позволяющие определять незначительные изменения показателя преломления прозрачных тел (газов, жидких и твердых тел) в зависимости от давления, температуры, примесей и т. д. Такие интерферометры получили название интерференционных рефрактометров. На пути интерферирующих лучей располагаются две одинаковые кюветы длиной l, одна из которых заполнена, например, газом с известным (n0), а другая — с неизвестным (nx) показателями преломления. Возникшая между интерферирующими лучами дополнительная оптическая разность хода D=(nx—n0)l . Изменение разности хода приведет к сдвигу интерференционных полос. Этот сдвиг можно характеризовать величиной
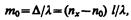
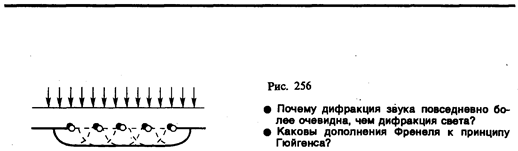
где m0 показывает, на какую часть ширины интерференционной полосы сместилась интерференционная картина. Измеряя величину m0 при известных l, n0 и l, можно вычислять nx или изменение nx–n0. Например, при смещении интерференционной картины на 1/5 полосы при l=10 см и l=0,5 мкм nx–n0 = 10–6, т.е. интерференционные рефрактометры позволяют измерять изменение показателя преломления с очень высокой точностью (до 1/1 000 000).
Применение интерферометров очень многообразно. Кроме перечисленного, они применяются для изучения качества изготовления оптических деталей, измерения углов, исследования быстропротекающих процессов, происходящих в воздухе, обтекающем летательные аппараты, и т. д. Применяя интерферометр, Майкельсон впервые провел сравнение международного эталона метра с длиной стандартной световой волны. С помощью интерферометров исследовалось также распространение света в движущихся телах, что привело к фундаментальным изменениям представлений о пространстве и времени.
Задачи
22.1. Определить, какую длину пути s1 пройдет фронт волны монохроматического света в вакууме за то же время, за которое он проходит путь s2=1,5 мм в стекле с показателем преломления n2=1,5. [2,25 мм]
22.2. В опыте Юнга щели, расположенные на расстоянии 0,3 мм, освещались монохроматическим светом с длиной волны 0,6 мкм. Определить расстояние от щелей до экрана, если ширина интерференционных полос равна 1 мм. [0,5 м]
22.3. На стеклянный клин (n=1,5) нормально падает монохроматический свет (l=698 нм). Определить угол между поверхностями клина, если расстояние между двумя соседними интерференционными минимумами в отраженном свете равно 2 мм. [0,4']
22.4. Установка для наблюдения колец Ньютона освещается монохроматическим светом, падающим нормально. При заполнении пространства между линзой и стеклянной пластинкой прозрачной жидкостью радиусы темных колец в отраженном свете уменьшились в 1,21 раза. Определить показатель преломления жидкости. [1,46]
22.5. На линзу с показателем преломления 1,55 нормально падает монохроматический свет с длиной волны 0,55 мкм. Для устранения потерь отраженного света на линзу наносится тонкая пленка. Определить: 1) оптимальный показатель преломления пленки; 2) толщину пленки. [1) 1,24; 2) 0,111 мкм]
22.6. В опыте с интерферометром Майкельсона для смещения интерференционной картины на 450 полос зеркало пришлось переместить на расстояние 0,135 мм. Определить длину волны падающего света. [0,6 мкм]
22.7. На пути одного из лучей интерференционного рефрактометра поместили откачанную трубку длиной 10 см. При заполнении трубки хлором интерференционная картина сместилась на 131 полосу. Определить показатель преломления хлора, если наблюдение производится с монохроматическим светом с длиной волны 0,59 мкм. [1,000773]
Глава 23Дифракция света
§ 176. Принцип Гюйгенса — Френеля
Дифракцией называется огибание волнами препятствий, встречающихся на их пути, или в более широком смысле — любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через небольшие отверстия в экранах и т. д. Например, звук хорошо слышен за углом дома, т. е. звуковая волна его огибает.
Явление дифракции объясняется с помощью принципа Гюйгенса (см. § 170), согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени.
Пусть плоская волна нормально падает на отверстие в непрозрачном экране (рис. 256). Согласно Гюйгенсу, каждая точка выделяемого отверстием участка волнового фронта служит источником вторичных волн (в однородной изотропной среде они сферические). Построив огибающую вторичных волн для некоторого момента времени, видим, что фронт волны заходит в область геометрической тени, т. е. волна огибает края отверстия.
Явление дифракции характерно для волновых процессов. Поэтому если свет является волновым процессом, то для него должна наблюдаться дифракция, т. е. световая волна, падающая на границу какого-либо непрозрачного тела, должна огибать его (проникать в область геометрической тени). Из опыта, однако, известно, что предметы, освещаемые светом, идущим от точечного источника, дают резкую тень и, следовательно, лучи не отклоняются от их прямолинейного распространения. Почему же возникает резкая тень, если свет имеет волновую природу? К сожалению, теория Гюйгенса ответить на этот вопрос не могла.
Принцип Гюйгенса решает лишь задачу о направлении распространения волнового фронта, но не затрагивает вопроса об амплитуде, а следовательно, и об интенсивности волн, распространяющихся по разным направлениям. Френель вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции вторичных волн.
Согласнопринципу Гюйгенса — Френеля, световая волна, возбуждаемая каким-либо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн. Френель исключил возможность возникновения обратных вторичных волн и предположил, что если между источником и точкой наблюдения находится непрозрачный экран с отверстием, то на поверхности экрана амплитуда вторичных волн равна нулю, а в отверстии — такая же, как при отсутствии экрана.
Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду (интенсивность) результирующей волны в любой точке пространства, т. е. определить закономерности распространения света. В общем случае расчет интерференции вторичных волн довольно сложный и громоздкий, однако, как будет показано ниже, для некоторых случаев нахождение амплитуды результирующего колебания осуществляется алгебраическим суммированием.
§ 177. Метод зон Френеля. Прямолинейное распространение света
Принцип Гюйгенса — Френеля в рамках волновой теории должен был ответить на вопрос о прямолинейном распространении света. Френель решил эту задачу, рассмотрев взаимную интерференцию вторичных волн и применив прием, получивший название метода зон Френеля.
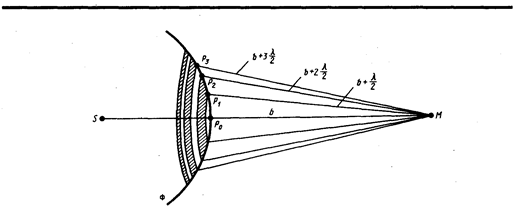
Найдем в произвольной точке М амплитуду световой волны, распространяющейся в однородной среде из точечного источника S (рис. 257). Согласно принципу Гюйгенса — Френеля, заменим действие источника S действием воображаемых источников, расположенных на вспомогательной поверхности Ф, являющейся поверхностью фронта волны, идущей из S (поверхность сферы с центром S). Френель разбил волновую поверхность Ф на кольцевые зоны такого размера, чтобы расстояния от краев зоны до М отличались на l/2, т. е. Р1М – Р0М = Р2М – Р1М = Р3М – Р2М = ... = l/2. Подобное разбиение фронта волны на зоны можно выполнить, проведя с центром в точке М сферы радиусами b + 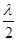 , b + 2
, b + 2 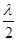 , b + 3
, b + 3 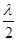 , ... . Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на l/2, то в точку М они приходят в противоположной фазе и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке М
, ... . Так как колебания от соседних зон проходят до точки М расстояния, отличающиеся на l/2, то в точку М они приходят в противоположной фазе и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке М
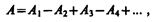 (177.1)
(177.1)
где А1, А2, ... — амплитуды колебаний, возбуждаемых 1-й, 2-й, ..., т-й зонами.
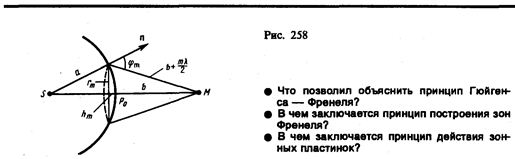
Для оценки амплитуд колебаний найдем площади зон Френеля. Пусть внешняя граница m-й зоны выделяет на волновой поверхности сферический сегмент высоты hm (рис. 258). Обозначив площадь этого сегмента через sm, найдем, что площадь m-й зоны Френеля равна Dsm = sm – sm–1, где sm–1 —площадь сферического сегмента, выделяемого внешней границей (m – 1)-й зоны. Из рисунка следует, что
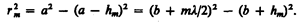 (177.2)
(177.2)
После элементарных преобразований, учитывая, что l<<a и l<<b, получим
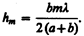 (177.3)
(177.3)
Площадь сферического сегмента и площадь т-й зоны Френеля соответственно равны
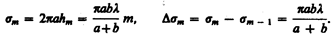 (177.4)
(177.4)
Выражение (177.4) не зависит от т, следовательно, при не слишком больших т площади зон Френеля одинаковы. Таким образом, построение зон Френеля разбивает волновую поверхность сферической волны на равные зоны.
Согласно предположению Френеля, действие отдельных зон в точке М тем меньше, чем больше угол jт (рис. 258) между нормалью n к поверхности зоны и направлением на М, т. е. действие зон постепенно убывает от центральной (около Р0) к периферическим. Кроме того, интенсивность излучения в направлении точки М уменьшается с ростом т и вследствие увеличения расстояния от зоны до точки М. Учитывая оба этих фактора, можем записать
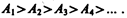
Общее число зон Френеля, умещающихся на полусфере, очень велико; например при а=b=10 см и l=0,5мкм 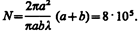 Поэтому в качестве допустимого приближения можно считать, что амплитуда колебания Аm от некоторой m-й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон, т. е.
Поэтому в качестве допустимого приближения можно считать, что амплитуда колебания Аm от некоторой m-й зоны Френеля равна среднему арифметическому от амплитуд примыкающих к ней зон, т. е.
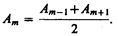 (177.5)
(177.5)
Тогда выражение (177.1) можно записать в виде
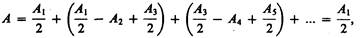 (177.6)
(177.6)
так как выражения, стоящие в скобках, согласно (177.5), равны нулю, а оставшаяся часть от амплитуды последней зоны ±Аm/2 ничтожно мала.
Таким образом, амплитуда результирующих колебаний в произвольной точке М определяется как бы действием только половины центральной зоны Френеля. Следовательно, действие всей волновой поверхности на точку М сводится к действию ее малого участка, меньшего центральной зоны.
Если в выражении (177.2) положим, что высота сегмента h<<а (при не слишком больших т), тогда 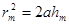 . Подставив сюда значение (177.3), найдем радиус внешней границы т-й зоны Френеля:
. Подставив сюда значение (177.3), найдем радиус внешней границы т-й зоны Френеля:
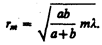 (177.7)
(177.7)
При а=b=10 см и l=0,5 мкм радиус первой (центральной) зоны r1 = 0,158 мм. Следовательно, распространение света от S к М происходит так, будто световой поток распространяется внутри очень узкого канала вдоль SM, т.е. прямолинейно. Таким образом, принцип Гюйгенса — Френеля позволяет объяснить прямолинейное распространение света в однородной среде.
Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используютсязонные пластинки —в простейшем случае стеклянные пластинки, состоящие из системы чередующихся прозрачных и непрозрачных концентрических колец, построенных по принципу расположения зон Френеля, т. е. с радиусами rm зон Френеля, определяемыми выражением (177.7) для заданных значений а, b и l (т = 0, 2, 4,... для прозрачных и т = 1, 3, 5,... для непрозрачных колец). Если поместить зонную пластинку в строго определенном месте (на расстоянии а от точечного источника и на расстоянии b от точки наблюдения на линии, соединяющей эти две точки), то для света длиной волны l она перекроет четные зоны и оставит свободными нечетные начиная с центральной. В результате этого результирующая амплитуда A=A1+A3+A5+... должна быть больше, чем при полностью открытом волновом фронте. Опыт подтверждает эти выводы: зонная пластинка увеличивает освещенность в точке М, действуя подобно собирающей линзе.
§ 178. Дифракция Френеля на круглом отверстии и диске
Рассмотримдифракцию в сходящихся лучах, илидифракцию Френеля, осуществляемую в том случае, когда дифракционная картина наблюдается на конечном расстоянии от препятствия, вызвавшего дифракцию.
1. Дифракция на круглом отверстии. Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране Э в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 259). Экран параллелен плоскости отверстия и находится от него на расстоянии b. Разобьем открытую часть волновой поверхности Ф на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами (см. (177.1) и (177.6)),
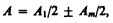
где знак плюс соответствует нечетным m и минус — четным т.

Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке В будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю. Если отверстие открывает одну зону Френеля, то в точке В амплитуда А=А1, т. е. вдвое больше, чем в отсутствие непрозрачного экрана с отверстием (см. § 177). Интенсивность света больше соответственно в четыре раза. Если отверстие открывает две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если m нечетное — то светлое кольцо), причем интенсивность в максимумах убывает с расстоянием от центра картины.
Расчет амплитуды результирующего колебания на внеосевых участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непрозрачным экраном. Если отверстие освещается не монохроматическим, а белым светом, то кольца окрашены.
Число зон Френеля, открываемых отверстием, зависит от его диаметра. Если он большой, тоАm<<A1 и результирующая амплитуда A=A1/2, т. е. такая же,как и при полностью открытом волновом фронте. Никакой дифракционной картины не наблюдается, свет распространяется,как и в отсутствие круглого отверстия, прямолинейно.
Дата добавления: 2015-12-16; просмотров: 586;
