Ламинарное движение шарика в жидкости. Формула Стокса

Стоксом было получено строгое решение задачи о ламинарном обтекания шарика безграничной жидкостью. В этом случае сила сопротивления F определяется формулой

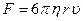, (14)

где h – коэффициент внутреннего трения жидкости, u –скорость шарика, r – радиус шарика.

Гидродинамический вывод формулы Стокса довольно сложен. Поэтому ограничимся анализом задачи с помощью теории размерности. На основании физических соображений и опыта можно считать, что сила F должна определяться параметрами h, u, r и плотностью жидкости r_ж. Искомый закон следует искать в виде степенного соотношения

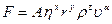, (15)

где А – безразмерный множитель, а x, y, z и a – подлежащие определению показатели степени. Выбор показателей степени определяется из того условия, что размерности левой и правой частей должны совпадать. Из опыта известно, сто при малых скоростях движения тела (ламинарное течение) сила сопротивления пропорциональна скорости (показатель степени a=1). Приравнивая показатели степени по массе, длине и времени в левой и правой частях уравнения (15), получим

1 = x + z, 1 = -x + 1 + y - 3z, -2 = -x - 1; (16)

откуда

x = 1, y = 1, z = 0. (17)

Таким образом получим

F=Ahru. (18)

Безразмерный множитель А не может быть определен из соображения размерности, но строгое решение этой задачи дает для этого множителя значение 6p.

Рассмотрим свободное падение шарика в вязкой жидкости. На шарик действуют сила тяжести, архимедова сила и сила вязкого трения, зависящая от скорости u. На основании второго закона механики будем иметь

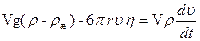, (19)

где V – объем шарика, r – его плотность, r_ж – плотность исследуемой жидкости, g – ускорение силы тяжести.

Решая это уравнение найдем

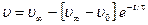, (20)

где 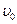– скорость шарика в момент начала его движения, которая в опытах обычно равна нулю, 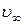– установившаяся скорость движения шарика, t – время релаксации. При этом величины 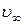и t соответственно равны

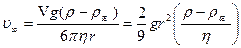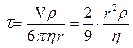; . (21)

Из уравнения (20) видно, что скорость шарика экспоненциально приближается к установившейся скорости 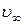. Установление скорости определяется временем релаксации t. Если время падения шарика в несколько раз больше времени релаксации (t>>t), то процесс установления скорости можно считать закончившимся.

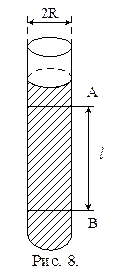
Поэтому для некоторой части пути, ограниченной метками А и В, где движение шарика будет равномерным, скорость шарика равна

u = l/t,(22)

где l – расстояние, t – время падения шарика между метками А и В.

Подставляя значение скорости в уравнение (21), получим:

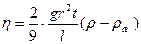. (23)

Данное уравнение справедливо лишь тогда, когда шарик падает в безграничной среде. Если шарик падает вдоль оси трубки радиуса R, то приходится учитывать влияние стенок, т.е. ввести поправки на влияние боковых стенок. Формула для определения коэффициента вязкости с учетом поправок принимает следующий окончательный вид:

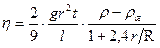. (24)

Соотношение (24) используется для определения вязкости жидкостей методом Стокса. Опуская шарик радиусом r в сосуд с исследуемой жидкостью, и измеряя время t прохождения шариком некоторого расстояния l можно найти коэффициент внутреннего трения жидкости h.

При выводе формулы Стокса предполагалось, что обтекание шарика жидкостью имеет ламинарный характер. Известно, что характер обтекания определяется значением числа Рейнольдса, которое определяется из формулы (6)

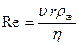. (25)

Для тел сферической формы обтекание будет ламинарным при условии Re <10.