Импульсные трансформаторы.

Импульсные трансформаторы (ИТ) применяются для передачи и формирования импульсов длительностью от единиц милисекунд до сотен микросекунд. Главным требованием, предъявляемым к ИТ при передаче импульсов, обычно является минимальное искажение формы передаваемого сигнала.

Допустим, что на первичную обмотку трансформатора в момент to(рис.1.20,а) поступает ступенчатое напряжение е . Трансформатор считаем идеальным в том смысле, что предполагается отсутствие паразитных параметров: омических сопротивлений обмоток (r1=r2=0), индуктивности рассеяния (Ls=0), паразитных емкостей (Cп=0), а также постоянство коэффициента магнитной проницаемости материала сердечника. Индуктивность L1первичной обмотки является конечной величиной и, следовательно, намагничивающий ток холостого хода не равен нулю. Если принять внутреннее сопротивление генератора импульсов е равным нулю, то конечная величина намагничивающего тока не будет влиять на форму передаваемого сигнала (см.рис.1.20,б).

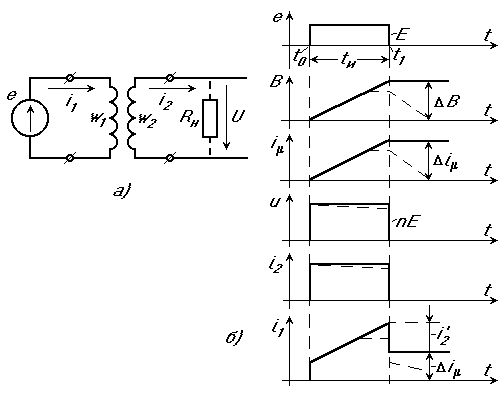
Рис.1.20. Схема идеального импульсного трансформатора (а) и форма напряжений и токов (б).

Если сопротивление нагрузки Rнотключить, то приложенное напряжение будет уравновешиваться ЭДС самоиндукции первичной обмотки, возникающей при протекании намагничивающего тока:

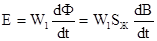(1.37)

где W1- число витков первичной обмотки; Ф, В и Sж- соответственно магнитный поток, магнитная индукция и поперечное сечение сердечника трансформатора.

Выходное напряжение U в этом случае будет равно ЭДС самоиндукции, возникающей во вторичной обмотке:

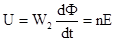, (1.38)

где W2- число витков вторичной обмотки; n - коэффициент трансформации.

Из формулы (1.37) следует, что магнитная индукция сердечника при передаче прямоугольных импульсов нарастает линейно

B = Kb·E ·t, (1.39)

где Kb= (W1·Sж)-1.

Таким образом, к моменту t1окончания импульса длительностью tиприращение магнитной индукции DB будет пропорционально площади импульса, т.е.

DB = Kb·E ·tu (1.40)

C учетом соотношений

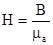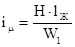, (1.41)

получаем, что намагничивающий ток, равный в данном случае току первичной обмотки, будет также нарастать линейно

i_m = Km·E ·t, (1.42)

где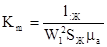

lж- средняя длина магнитопровода; ma = m·mo- абсолютная магнитная проницаемость; mo- относительная магнитная проницаемость; m - магнитная постоянная.

Соотношения (1.41) и (1.42) определяют эквивалентную схему замещения ИТ, изображенную на рис.1.21. Индуктивность намагничивания Lmопределяют из равенства

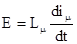(1.43)

в следующем виде

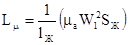, (1.44)

В рассматриваемом идеальном случае L_m = L1, напряжение на выходе эквивалентной схемы

U' = U/n, (1.45)

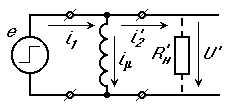
Рис.1.21. Схема замещения идеального трансформатора.

Из эквивалентной схемы (рис.1.21) можно определить приращение намагничивающего тока за время импульса, а именно

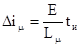, (1.46)

Если подключить нагрузочное сопротивление Rнк вторичной обмотке, то в цепи вторичной обмотки потечет ток i2, стремящийся размагнитить сердечник на величину, пропорциональную нагрузочным ампервиткам i2·w2. Однако в связи с тем, что скорость изменения магнитного потока должна остаться постоянной в соответствии с соотношением (1.37), намагничивающие ампервитки должны увеличиться в соответствии с равенством

i1 ·W1= im·W1+ i2 ·W2, (1.47)

Ток i2определяется выражением

, (1.48)

Следовательно, чтобы эквивалентная схема (рис.1.21) правильно отражала ток i1, протекающий по первичной обмотке

i₁ = i_m + i₂', (1.49)

где i₂' = n×i₂,

необходимо на выходе подключить эквивалентную нагрузку

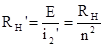, (1.50)

Таким образом, в рассматриваемом идеальном случае передачи прямоугольного импульса DB, DH и Di_m будут определяться лишь конструкцией трансформатора и материалом его магнитопровода и не будут зависеть от нагрузки. От Rнбудет зависеть лишь ток i1. В реальных условиях наличие тока намагничивания i_m определяет искажение формы выходного сигнала (снижение вершины импульса), в связи с чем индуктивность L_m не должна быть меньше определенной величины.

После окончания импульса (момент t1) принятая идеализация теряет смысл, т.к. после выключения напряжения е происходит короткое замыкание первичной обмотки и токи i1, i_m, i2, а следовательно, и магнитная индукция В должны остаться постоянными и равными i1(t1), i2(t1), i_m(t1), B(t1). На практике всегда происходит рассеяние магнитной энергии, т.е. убывание тока imв соответствии со структурой сопротивлений, включенных в обмотки трансформатора. Возможный характер процессов с учетом наличия омических сопротивлений в цепи первичной обмотки трансформатора показан пунктирными кривыми на рис.120,б.

Рассмотренные идеализированные процессы передачи импульсов трансформатором на практике осложняются явлением гистерезиса, влиянием вихревых токов, рассеянием электромагнитной энергии и влияние токов смещения в обмотках ИТ. Рассмотрим сущность наиболее существенных из этих явлений и методы их учета.

Явление гистерезиса. Для магнитных материалов, из которых изготавливаются сердечники ИТ, связь между B и H является нелинейной и характеризуется шлейфами гистерезиса предельного симметричного цикла. Верхняя половина типового шлейфа гистерезиса приведена на рис.1.22. Если отсутствует остаточное намагничивание сердечника, то при передаче через трансформатор первого из последовательности импульсов площадью E·tиизображающая точка перемещается из точки О в точку B1, являющуюся пересечением основной кривой намагничивания с горизонтальной прямой B=DB, где приращение индукции DB определяется формулой (1.40). После окончания первого импульса изображающая точка перейдет в точку Bo1по нисходящей ветви B1-Bo1симметричного цикла. При поступлении второго импульса изображающая точка перемещается в точку B2вначале по восходящей ветви симметричного цикла, примыкающей к основной кривой намагничивания, а затем по нисходящей ветви, причем разность величин индукции в точках B2и Bo1также равна DB. Этот процесс нарастания остаточной магнитной индукции при поступлении очередного импульса будет продолжаться до тех пор, пока изображающая точка не достигнет точки О', соответствующей остаточной индукции Boпредельного цикла. После этого при передаче каждого из импульсов напряжения изображающая точка будет перемещаться между точками О' и M по предельной петле частного (несимметричного) цикла, заштрихованной на рис.1.22, наклон которой будет определяться величиной DB. Таким образом, среднее в пределах импульса значение магнитной проницаемости, называемой импульсной магнитной проницаемостью mDбудет определяться соотношением

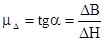(1.51)

Рис.1.22. Кривые намагничивания сердечника ИТ.

Проницаемость mDвсегда меньше нормальной (статической) магнитной проницаемости в точке М (mн=Bm/DH), причем разница между ними тем больше, чем выше величина остаточной индукции Bo. Чтобы избежать искажения формы передаваемых импульсов, приращение DB индукции за время импульса не должно превышать разности

DBmax= Bs- Bo,

где Bs- индукция насыщения данного материала.

Таким образом, материал сердечника ИТ должен обладать возможно более низкой остаточной индукцией Bo, высоким значением Bsи mD.

Эквивалентная схема реального трансформатора.

На рис.1.23 приведена эквивалентная схема трансформатора, учитывающая явление гистерезиса, вихревые токи, рассеяние электромагнитной энергии.

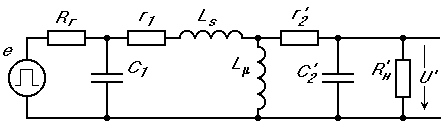
Рис.1.23. Эквивалентная схема трансформатора.

Индуктивность рассеяния Lsвключена до индуктивности намагничивания, так как она невелика [10]. Параметры этой эквивалентной схемы определяются следующими соотношениями

Ls=(1-K2)·L1 @2·L1(1-K), Lm=K2·L1 @L1,

C2'=C2·n2/K2 @C2·n2, r2'=r2·K2/n2 @r2 / n2,

Rн'=Rн·K2/n2 @Rн/n2, (1.52)

где C1и C2- паразитные емкости обмоток трансформатора,

К³0,99 - коэффициент связи.

В связи с этим индуктивность рассеяния Lsимеет величину порядка 1% от L_m и может быть от десятков долей микрогенри до нескольких десятков микрогенри. L_m определяется расчетным путем, а также экспериментально резонансным методом или методом ударного возбуждения.

Суммарное сопротивление обмоток r1 + r2'@ 2·r1составляет обычно единицы процентов от величины Rн' и Rгим, как правило пренебрегают. Влияние явлений гистерезиса и вихревых токов учитывается в изменении параллельной ветви схемы (рис.1.23), включающей L_m (см. выше).

Переходные процессы в схеме рис.1.23 описываются дифференциальным уравнением 4-го порядка. Поэтому анализ быстрых процессов, имеющих место при формировании фронтов импульсов , и сравнительно медленных процессов формирования (или передачи) вершины импульса проводится отдельно.

Формирование фронтов импульса. Для определения формы фронтов выходного импульса используется эквивалентная схема, представленная на рис.1.24, полученная из схемы рис.1.23 исключением индуктивности намагничивания Lmи суммарного активного сопротивления обмоток.

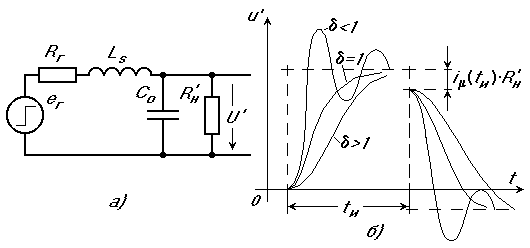
Рис.1.24. Эквивалентная схема трансформатора для определения фронтов выходного импульса (а) и формы выходного напряжения (б).

В схеме рис.1.24 Co=C1+C2' суммарная паразитная емкость обмоток.

Значения корней характеристического уравнения, определяющего характер переходных процессов в схеме рис.1.24,а определяются соотношениями

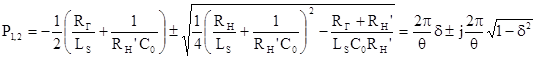, (1.53)

где , ,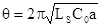

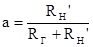
В зависимости от величины подкоренного выражения в (1.53) характер установления стационарной амплитуды Um=a·E будет апериодическим (d > 1), критическим (d = 1) или колебательным (d<1). На практике обычно выбирают d = 0,6...0,7, т.е. процесс - колебательный затухающий, что дает наименьшую длительность фронта.

Формирование вершины импульса. Для определения искажения формы вершины импульса из эквивалентной схемы рис.1.23 исключаются паразитные емкости С1и С2', а также индуктивность рассеяния Ls.

Закон изменения вершины импульса после поступления на вход схемы ступенчатого напряжения Е будет определяться экспонентой

U' = Uo·e -t/t, (1.54)

где 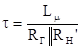, Uo= a·E.

Для получения малых искажений вершины импульса должно выполняться условие t >> tи, тогда можно ограничиться линейным членом разложения экспоненты (1.54) в степенной ряд. Оценку искажений удобно характеризовать относительным снижением вершины к концу импульса tи:

, (1.55)

Хвост импульса, изображенный на рис.1.25,б образуется за счет падения напряжения на сопротивлении Rн' от убывания намагничивающего тока.

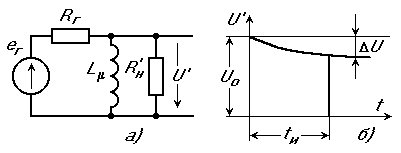
Рис.1.25. Эквивалентная схема ИТ для определения искажений вершины импульса (а) и форма выходного напряжения (б).