АНАЛИТИЧЕСКИЙ МЕТОД
КОНТРОЛЬНО-ИЗМЕРИТЕЛЬНЫЕ ПРИБОРЫ И
УСТРОЙСТВА
Для контроля за состоянием среды, протекающей по трубопроводам судовых систем, используют манометры, вакуумметры и термометры. Манометрами измеряют давление среды выше атмосферного, а вакуумметрами — ниже атмосферного. Ртутные термометры служат для измерения температуры среды. На шкалах манометров и термометров красной чертой указываются наибольшие допустимые рабочие параметры.
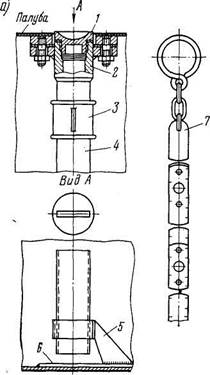
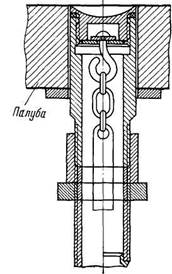
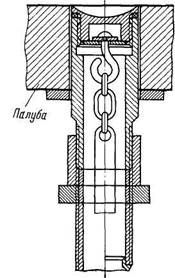
Количество жидкости в цистернах измеряют главным образом измерительными трубами с метрштоками (измерительными рейками) и уровнемерами (указательными колонками и поплавковыми указателями уровня). Уровнемеры применяют в основном для измерения высоты уровня жидкости во вкладных цистернах, устанавливаемых или навешиваемых на фундаменты. Положение уровня жидкости в корпусных цистернах, являющихся неотъемлемой частью корпуса судна, преимущественно замеряют с помощью измерительных труб. Типовые конструкции измерительных труб, выведенных на палубу, показаны на рис. 27.
Измерительная труба 4 (рис. 27, а) посредством соединительной муфты 3 крепится к палубной втулке 2, снабженной крышкой 1. Нижний конец трубы закреплен на кронштейне 5. Для измерения уровня жидкости в трубу опускают метршток 7. Чтобы не допустить повреждения обшивки от его ударов, под нижним отверстием трубы приваривают планку 6.
Метрштоки выполняют в виде металлической рейки или складными в виде линейки, состоящей из отдельных звеньев. Они могут быть градуированы в линейных
| 
|
Рис. 27. Измерительные трубы
единицах, единицах объема или массы жидкости. Метршток прикрепляют к крышке измерительной трубы или размещают вблизи трубы. Протарированные для данной емкости метрштоки называются штатными (рис. 27, б).
Измерительные трубы выводят из самых глубоких мест цистерн по прямой линии. При необходимости они могут иметь погибь, не препятствующую прохождению метрштока.
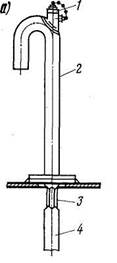
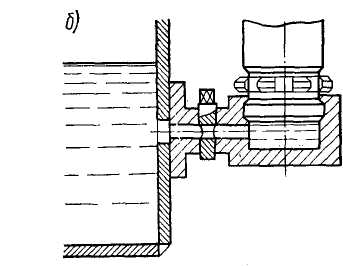
Часто измерительные трубы совмещают с воздушными, обеспечивающими выход воздуха из цистерны при заполнении и подвод атмосферного воздуха при удалении из нее жидкости (рис. 28, а). Измерительная труба 4 крепится к воздушной 2, имеющей отверстие с пробкой 1 для опускания метрштока в цистерну. В верхней части измерительной трубы (под настилом цистерны) сделаны продольные 3 прорези для выхода воздуха.
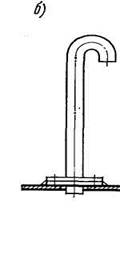
На рис. 28, б показана воздушная труба, устанавливаемая отдельно на настиле (палубе) цистерны. Чтобы исключить попадание через трубу в цистерну загрязнений или забортной воды, наружный конец ее выполняют в виде гуська (загибают на 180°). Иногда его снабжают защитным колпаком. Воздушные трубы цистерны должны быть выведены из верхней ее части и, как правило, из места, наиболее удаленного от наполнительного трубопровода. Цистерны, простирающиеся от борта до борта, должны оборудоваться воздушными трубами у обоих бортов.
|
|
Суммарная площадь сечения воздушных труб цистерны, заполняемой гравитационным способом, должна быть не менее суммарной площади сечения ее наполнительных труб. Площадь сечения воздушных труб цистерны, заполняемой судовыми или береговыми насосами, должна составлять не менее 1,25 площади сечения ее наполнительного трубопровода. При диаметре наполнительного трубопровода менее 50 мм диаметр воздушной трубы может не превышать диамет ра наполнительной трубы. Если цистерна, заполняемая судовыми или береговыми насосами, оборудована переливной трубой, суммарная площадь
сечения воздушных труб цистерны должна быть не менее 1/3 площади сечения наполнительного трубопровода. Во всех случаях диаметр воздушной трубы для водяных цистерн должен быть не менее 40 мм.
| Рис. 28. Воздушные трубы |
Кроме цистерн для хранения жидкости, воздушными трубами оборудуют также коффердамы, ледовые и кингстонные ящики. Воздушные трубы ледовых и кингстоновых ящиков снабжают запорными клапанами, устанавливаемыми непосредст-
венно на ящиках.
|

|
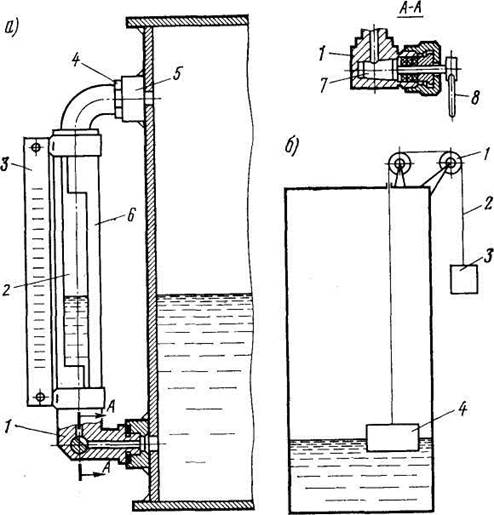
Рис. 29. Уровнемеры
Воздушные и измерительные трубы выполняют из стали или из легкого сплава.
Рассмотрим устройство указательной колонки и поплавкового указателя уровня.
Указательные колонки работают по принципу сообщающихся сосудов. Устройство простейшей колонки для воды дано на рис. 29, а. Цилиндрическая стеклянная трубка 2 диаметром 15x3,5 мм нижним концом закреплена и уплотнена в бронзовом корпусе 1, а верхним герметически соединена с металлической трубкой штуцера 4. Трубка защищена от повреждения кожухом 6. Концы колонки ввернуты в приварыши 5, расположенные на стенке цистерны. Количество воды, находящееся в цистерне, определяют по шкале 3. От цистерны колонку отсоединяют пробкой 7 с помощью насаженной на нее рукоятки 8.
На рис. 29, б приведена схема поплавкового указателя уровня. При изменении высоты уровня жидкости в цистерне меняется положение поплавка 4 и противовеса 3, связанных гибким тросиком 2. Для уменьшения трения тросик перемещается по роликам 1. Снаружи цистерны устанавливается градуированная шкала с нулевой точкой наверху и максимальной отметкой внизу. При изменении уровня жидкости перемещается поплавок и связанный с ним тросиком противовес, показывающий на шкале уровень жидкости в цистерне.
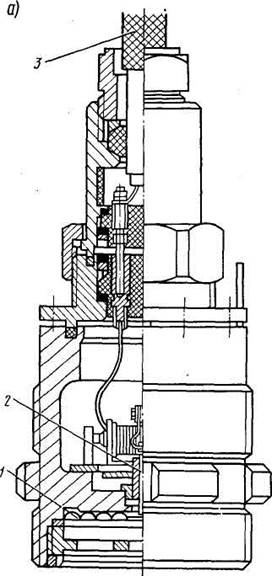
В последние годы начали широко внедрять дистанционные указатели уровня различных типов. Ограничимся рассмотрением прибора типа УУЖЭК (указатель уровня жидкости электрический корабельный), предназначенного для измерения в цистернах и отсеках судна уровня воды, жидкого топлива, масла и др. Принцип действия прибора основан на упругих свойствах мембраны 1 (рис. 30, а), прогибающейся под давлением столба жидкости, и преобразовании этого прогиба с помощью передаточного механизма 2 и потенциометра, введенного в цепи датчика и измерителя.
|
|
Изменение сопротивлений элементов схемы вызывает изменение токов, протекающих по рамкам магнитоэлектрического измерителя. Стрелка его отклоняется на угол, пропорциональный измерению давления, и показывает уровень по шкале, протарированной в метрах водяного столба (м вод. ст.).
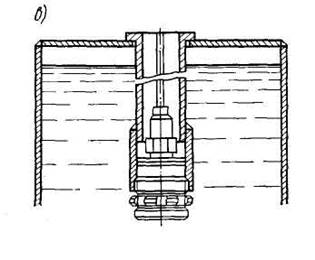
Рис. 30. Датчик прибора типа
УУЖЭК
Воспринимающий гидростатическое давление датчик и дистанционный электрический измеритель соединены кабелем 3.
Прибор является виброустойчивым и может работать в условиях качки. Его выпускают с различным диапазоном измерения в пределах 0—10 м. Датчик размещают снаружи цистерны в специальном патрубке с фланцем (рис. 30, б) на уровне, принимаемом условно для данной цистерны за нуль. Допускается установка его внутри цистерны в трубе, как показано на рис. 30, в.
Кроме типовых контрольно-измерительных приборов и устройств, в судовых системах применяют специальные приборы, как, например сигнализаторы уровня, психрометры и др. Они рассматриваются совместно с системами, в которых используются.
1.7 ОСНОВЫ ГИДРАВЛИЧЕСКОГО РАСЧЕТА ТРУБОПРОВОДОВ
ОСНОВНЫЕ РАСЧЕТНЫЕ ЗАВИСИМОСТИ И ХАРАКТЕРИСТИКИ
В основе гидравлического расчета трубопроводов лежат известные из гидравлики уравнение неразрывности и уравнение Бернулли.
Уравнение неразрывности (сплошности) потока для случая несжимаемой жидкости имеет вид
f1 υ 1 f2 υ 2 const, (10)
где f1, f2 — площади 1-го и 2-го сечений трубы;
υ 1, υ 2 — средние скорости движения жидкости в 1-м и 2-м сечениях.
Уравнение (10) показывает, что если в трубопроводе нет притоков и отводов, то расход жидкости в любом сечении является постоянным, а следовательно, средние скорости будут обратно пропорциональны площадям сечений трубы: υ 1/ υ 2 f2/ f1.
Уравнение Бернулли выражает закон сохранения энергии движущейся жидкости. В случае установившегося движения несжимаемой жидкости для 1-го и 2-го сечений потока относительно произвольно выбранной горизонтальной плоскости сравнения оно запишется в следующем виде:
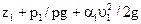
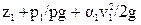
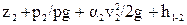 , (11)
, (11)
где 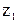 ,
, 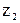 — высоты расположения центров тяжести 1-го и 2-го сечений потока
— высоты расположения центров тяжести 1-го и 2-го сечений потока
над плоскостью сравнения;
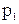 ,
, 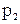 — давления в центрах тяжести 1-го и 2-го сечений;
— давления в центрах тяжести 1-го и 2-го сечений;
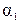 ,
, 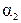 — коэффициенты, учитывающие неравномерность распределения
— коэффициенты, учитывающие неравномерность распределения
скоростей по сечению потока (для турбулентного режима 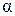 =1,045
=1,045
и практически принимается 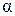 = 1, для ламинарного режима
= 1, для ламинарного режима 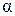 = 2);
= 2);
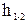 — потерянная удельная энергия потока или потеря напора на участке
— потерянная удельная энергия потока или потеря напора на участке
1—2
Таблица 3
| Температура, °С | Значения V106 при содержании солей по массе | |||
| 0 (пресная вода) | ||||
| 1,789 | 1,804 | 1,815 | 1,825 | |
| 1,516 | 1,530 | 1,544 | 1,556 | |
| 1,306 | 1,320 | 1,334 | 1,348 | |
| 1,145 | 1,152 | 1,165 | 1,179 | |
| 1,007 | 1,019 | 1,032 | 1,045 | |
| 0,897 | 0,905 | 0,917 | 0,930 | |
| 0,805 | 0,816 | 0,827 | 0,838 |
Как известно, ламинарный режим течения наблюдается при числе Рейнольдса Re < 2300, тогда как турбулентный при Re > 2300. Число Рейнольдса Re = υ d/n, где υ — скорость течения жидкости в трубе, м/с; d — внутренний диаметр трубы, м; n — коэффициент кинематической вязкости, м2/с. Для различных капельных жидкостей n зависит главным образом от температуры, уменьшаясь с ее повышением. Значения коэффициента n 106 для воды приведены в табл. 3.
Основным видом течения жидкости в трубопроводах судовых систем является турбулентное. Ламинарный режим течения наблюдается в трубопроводах, транспортирующих жидкости, обладающие значительной вязкостью (мазут, масло, нефть).
По физическому смыслу все члены уравнения (11) представляют собой удельные энергии (отнесенные к единице веса жидкости); так, член z есть удельная потенциальная энергия положения жидкости, член p/pg — удельная потенциальная энергия давления и член 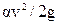 — удельная кинетическая энергия потока в данном сечении. Весь трехчлен z + p/pg+
— удельная кинетическая энергия потока в данном сечении. Весь трехчлен z + p/pg+ 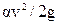 выражает собой полную удельную энергию, которую имеет поток в данном поперечном сечении, т. е. полный гидродинамический напор, выражаемый в метрах столба жидкости. Величина
выражает собой полную удельную энергию, которую имеет поток в данном поперечном сечении, т. е. полный гидродинамический напор, выражаемый в метрах столба жидкости. Величина 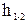 представляет собой уменьшение удельной энергии потока на длине между 1-м и 2-м сечением, затрачиваемой на преодоление сопротивления движению жидкости.
представляет собой уменьшение удельной энергии потока на длине между 1-м и 2-м сечением, затрачиваемой на преодоление сопротивления движению жидкости.
Потери напора h складываются из потерь на трение hт в прямых участках трубопровода и потерь в местных сопротивлениях (задвижке, клапане, колене и др.) hм. Следовательно, можно написать
h = hт + hм. (12)
Потери напора на трение (м) в прямых цилиндрических трубах определяют по формуле Дарси — Вейсбаха
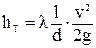 ,
,
где 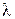 - коэффициент гидравлического трения;
- коэффициент гидравлического трения;
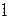 - длина прямой трубы, м;
- длина прямой трубы, м;
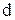 - внутренний диаметр трубы, м;
- внутренний диаметр трубы, м;
υ - средняя скорость жидкости, м/с
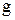 - ускорение свободного падения, м/с2.
- ускорение свободного падения, м/с2.
При определении потерь на трение (м) в трубах прямоугольного сечения используют формулу
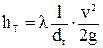 ,
,
где dr — гидравлический диаметр, м.
Для прямоугольного канала с размерами сторон а и b гидравлический диаметр
dr = 2аb /( а + b). (15)
Трубы прямоугольного сечения применяют в системах вентиляции и кондиционирования воздуха.
При выполнении расчетов трубопроводов необходимо знать коэффициент гидравлического трения 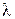 . В общем случае он является функцией числа Рейнольдса Re и шероховатости стенок трубы, по которой протекает жидкость.
. В общем случае он является функцией числа Рейнольдса Re и шероховатости стенок трубы, по которой протекает жидкость.
За меру шероховатости принимают расчетную высоту выступа k, которая называется абсолютной шероховатостью и измеряется в миллиметрах. Для труб промышленного производства, имеющих неравномерное распределение выступов и впадин, волнистость, используют понятие эквивалентной шероховатости kэ. Значение ее получают расчетом, исходя из условия эквивалентности гидравлического сопротивления труб одинаковых длин и внутренних диаметров, одна из которых имеет равномерную зернистую шероховатость, а другая — неравномерную.
Отношение абсолютной шероховатости k(kэ) к характерному линейному поперечному размеру трубы (обычно к диаметру) называется относительной шероховатостью 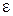 , т. е.
, т. е. 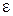 = k/d или
= k/d или 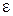 = kэ/d.
= kэ/d.
Для ламинарного режима течения независимо от 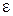 значение
значение 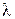 определяют по формуле
определяют по формуле
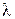 = 64/Re. (16)
= 64/Re. (16)
Для технически гладких трубопроводов, т. е. когда kэ ≈ 0 и 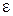 ≈ 0 при Re > 2300
≈ 0 при Re > 2300
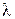 = (1,8 Re – 1,5)-2. (17)
= (1,8 Re – 1,5)-2. (17)
Как частный случай для указанных трубопроводов при 2300 < Re < 105 коэффициент 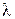 может быть найден по формуле
может быть найден по формуле
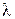 = 0,3164 Re - 0,25 (18)
= 0,3164 Re - 0,25 (18)
Для шероховатых труб при условии, что Re > 2300, т. е. для всей области турбулентного течения, коэффициент 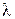 можно определить по формуле
можно определить по формуле
λ=0,1 (1,46 kэ/d+100/Re)0,25. (19)
Эквивалентная шероховатость стальных труб, не бывших в эксплуатации, изменяется в пределах от 0,02 до 0,2 мм в зависимости от технологии их изготовления, срока хранения и т. д. [2]. Для новых алюминиевых труб значение kэ принимают в среднем равным 0,025 мм.
Коэффициент λ можно также найти по графику рис. 31, на котором представлены кривые λ=f(Re,d/kэ). Кривая предельных значений чисел Рейнольдса Reпp показывает, что в области справа от нее коэффициент λ зависит только от относительной шероховатости.
Местные потери напора (м) вычисляют по формуле
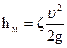 (20)
(20)
где 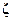 – коэффициент местного сопротивления;
– коэффициент местного сопротивления;
υ – средняя скорость жидкости на входе в местное сопротивление или выходе из него, м/с.
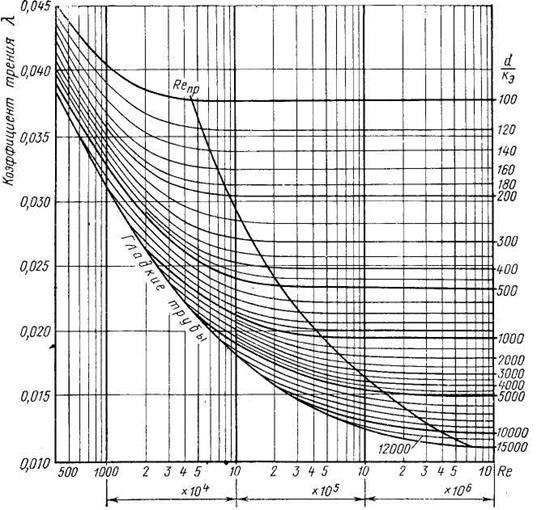
Если на отдельном участке трубопровода имеется несколько местных сопротивлений, то потерю напора на нем определяют как сумму потерь напора в отдельных местных сопротивлениях, т. е.
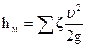 (21)
(21)
Такое суммирование местных сопротивлений справедливо, если они удалены одно от другого на расстоянии 10 диаметров трубы. При меньшем расстоянии
Числа Re
Рис. 31. Зависимость коэффициента гидравлического трения от числа Рейнольдса для стальных труб разного диаметра
между местными сопротивлениями наблюдается их взаимное влияние, выражающееся в увеличении коэффициента 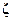 . Однако в практике расчета трубопроводов этим влиянием обычно пренебрегают и расчет ведут по формуле (21).
. Однако в практике расчета трубопроводов этим влиянием обычно пренебрегают и расчет ведут по формуле (21).
Коэффициент местного сопротивления 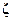 есть величина безразмерная и в общем случае является функцией числа Рейнольдса потока и вида местного сопротивления (крана, клапана, тройника и др.), т. е.
есть величина безразмерная и в общем случае является функцией числа Рейнольдса потока и вида местного сопротивления (крана, клапана, тройника и др.), т. е. 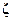 = f (Re, вид местного сопротивления).Несмотря на наличие большого количества экспериментальных материалов и теоретических исследований, общие зависимости для
= f (Re, вид местного сопротивления).Несмотря на наличие большого количества экспериментальных материалов и теоретических исследований, общие зависимости для 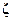 , относящиеся ко всем видам местных сопротивлений, еще не получены.
, относящиеся ко всем видам местных сопротивлений, еще не получены.
Для некоторых наиболее простых видов местных сопротивлений (резкое расширение, течение жидкости в конических трубах, диафрагмы и др.) получены теоретические формулы, по которым определяют потери напора в них. В большинстве случаев 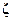 находят экспериментальным путем. При выборе коэффициента местного сопротивления в первую очередь следует учитывать режим движения потока, т. е. значение Re потока, при котором были получены значения
находят экспериментальным путем. При выборе коэффициента местного сопротивления в первую очередь следует учитывать режим движения потока, т. е. значение Re потока, при котором были получены значения 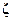 , пределы применимости опытных данных, а также, к какой скорости препятствий они отнесены. Практически при Re ≥ 105 изменением коэффициента
, пределы применимости опытных данных, а также, к какой скорости препятствий они отнесены. Практически при Re ≥ 105 изменением коэффициента 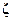 можно пренебречь и считать, что он является величиной постоянной. Значения коэффициентов
можно пренебречь и считать, что он является величиной постоянной. Значения коэффициентов 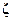 , представляют либо в табличной форме, либо в виде графиков или в виде экспериментальной формулы.
, представляют либо в табличной форме, либо в виде графиков или в виде экспериментальной формулы.
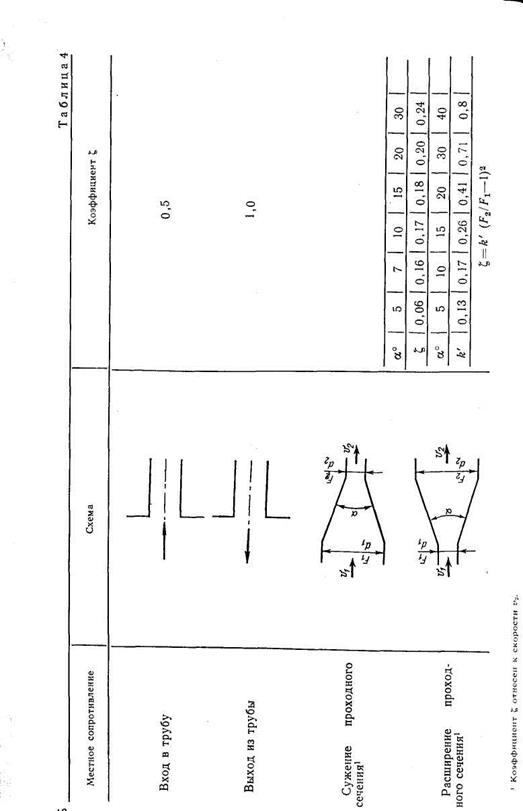
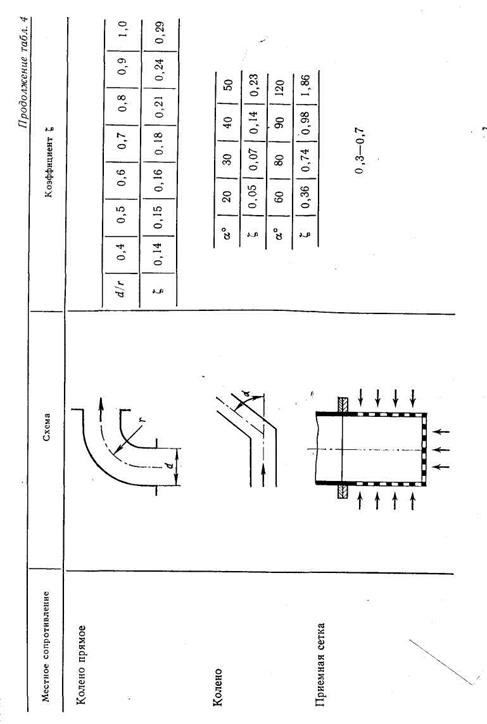
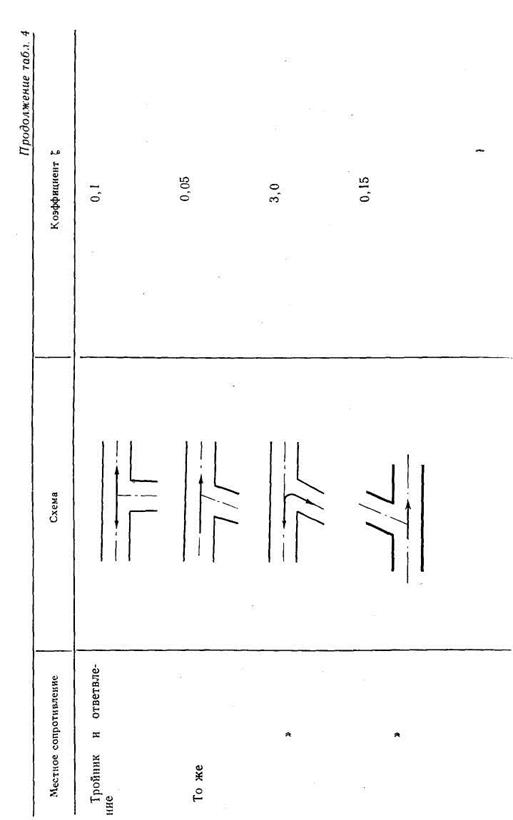
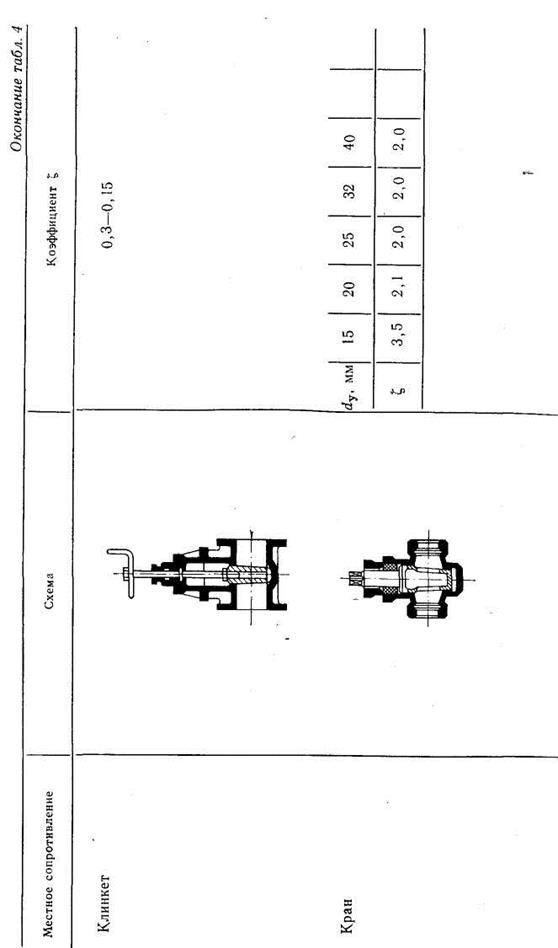
В табл. 4 приведены значения коэффициентов местных сопротивлений 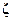 для некоторых элементов судовых водопроводов. Подробные сведения по различным видам гидравлических сопротивлений содержатся в справочнике И. Е. Идельчика [10]. Значения коэффициентов сопротивления
для некоторых элементов судовых водопроводов. Подробные сведения по различным видам гидравлических сопротивлений содержатся в справочнике И. Е. Идельчика [10]. Значения коэффициентов сопротивления 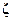 арматуры часто указывают на чертежах завода — поставщика арматуры.
арматуры часто указывают на чертежах завода — поставщика арматуры.
Выведем формулу для построения характеристики трубопровода. Потери напора в трубопроводе можно выразить зависимостью
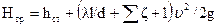 ,
,
где 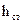 — статическая высота подачи, равная сумме геометрической и манометрической высот, причем под последней подразумевается высота, соответствующая избыточному давлению в системе (пневмоцистерне, магистрали водотушения и др.); 1 — учитывает потерю с выходной скоростью в случае концевой трубы.
— статическая высота подачи, равная сумме геометрической и манометрической высот, причем под последней подразумевается высота, соответствующая избыточному давлению в системе (пневмоцистерне, магистрали водотушения и др.); 1 — учитывает потерю с выходной скоростью в случае концевой трубы.
Так как при расходе Qтр через трубопровод скорость
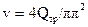 , то
, то 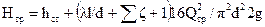
Для каждого данного трубопровода величина 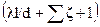
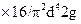 является постоянной. Окончательно получим
является постоянной. Окончательно получим
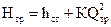 . (22)
. (22)
Это и есть уравнение характеристики трубопровода.
На рис. 32 характеристика трубопровода изображена кривой 2. Если на эту характеристику нанести характеристику насоса 1, то можно определить его режим работы. Точка А пересечения характеристик насоса и трубопровода называется рабочей точкой. Она показывает, что
|
|
|

|
|
насос, работая на данный трубопровод, будет обеспечивать подачу Q1, и напор Н1. Изменение характеристики трубопровода вызывает перемещение точки А на характеристике насоса и, следовательно, изменение режима работы последнего.
Характеристику Н— Q насоса строят по результатам испытаний его на стенде при постоянной частоте вращения n (мин-1). Такие характеристики приводятся в каталогах на насосы.
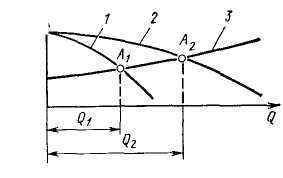
Представим теперь, что в трубопровод жидкость подается не одним, а двумя насосами, подключенными к нему параллельно. При параллельном соединении обеспечивается увеличенная подача жидкости в трубопровод. Будем считать, что насосы одинаковые и характеристика Н— Q каждого из них изображается кривой 1 (рис. 33, а). Суммарная характеристика 2 двух параллельно работающих насосов получается сложением их подач при одинаковых напорах. Нанося на эти характеристики характеристику трубопровода 3, получим рабочие точки А1 и А2, которые определяют количество жидкости, перекачиваемое по трубопроводу од ним (подача Q1) и двумя (подача Q2) параллельно работающими насосами.
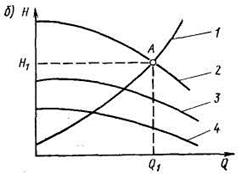
На практике встречаются случаи, когда насосы работают последовательно. При последовательном соединении повышается напор насосной установки (рис. 33, б). На рисунке кривая 4 — характеристика одного насоса, а кривая 3—характеристика другого. Суммарная характеристика 2 двух последовательно работающих насосов получается сложением их напоров при одинаковой подаче. Пересечение характеристики 2 насосов с характеристикой 1 трубопровода в точке А определяет режим работы двух последовательно включенных насосов. Последовательное соединение насосов применяют на танкерах при выкачке вязкого нефтегруза на некоторые нефтебазы, расположенные на значительном расстоянии от причала. Форма характеристик Н— Q , изображенных на рис. 32 и 33, свойственна лопастным насосам.
 n= const n= const
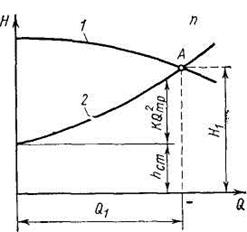 Рис. 32. К определению рабочего
режима насоса
Рис. 32. К определению рабочего
режима насоса
| 
| ||
| Рис. 33. Графики совместной работы насосов | |||
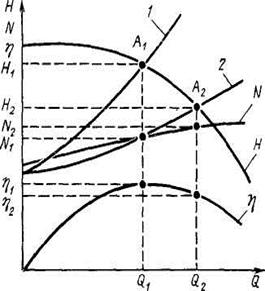 Рис. 34. К определению показателей
работы насоса
Рис. 34. К определению показателей
работы насоса
| У поршневого насоса подача весьма мало зависит от создаваемого им напора, т. е. насос имеет жесткую характеристику. Незначительное уменьшение подачи поршневого насоса с увеличением напора объясняется возрастанием протечек жидкости внутри насоса. На практике этим уменьшением подачи обычно пренебрегают и характеристику Н— Q поршневого насоса изображают в виде прямой, параллельной оси ординат. Для суждения об экономичности работы лопастного насоса в системе на характеристику трубопровода наносят характеристики Н— Q, Н— Q и η — Q насоса (рис.34). Пользуясь такими | ||
| характеристиками, можно при каждой данной подаче Q определить не только необходимый напор Н насоса, но также его мощность N и к. п. д. η. Так, например, рабочей точке А1 соответствует подача Q1 напор Н1 мощность N1 и к. п. д. η1; рабочей точке А2— Q2, Н2, N2 и η2 . Как видно, на трубопровод 1 насос будет работать более экономично, чем на трубопровод 2, поскольку η1 > η2 . При подборе насоса для судовой системы стремятся к тому, чтобы он на расчетном режиме имел максимальный к. п. д. | |||
МЕТОДЫ ГИДРАВЛИЧЕСКОГО РАСЧЕТА ТРУБОПРОВОДОВ
Одним из главных вопросов при проектировании судовых систем является гидравлический расчет трубопроводов. Он служит основой для выбора внутренних диаметров труб, скоростей движения жидкостей, подачи и напора гидравлических механизмов (насоса, вентилятора).
| При проектировании судовых систем встречаются разнообразные случаи гидравлического расчета трубопроводов. Можно выделить 2 основных случая: напор, расходуемый на преодоление гидравлических сопротивлений в трубопроводе, является искомой величиной, что чаще всего бывает на практике; напор, расходуемый на преодоление гидравлических сопротивлений в системе, является заранее заданной величиной. В первом случае определяют |
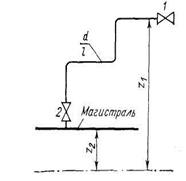
| Рис. 35. Расчетная схема простого трубопровода |
|
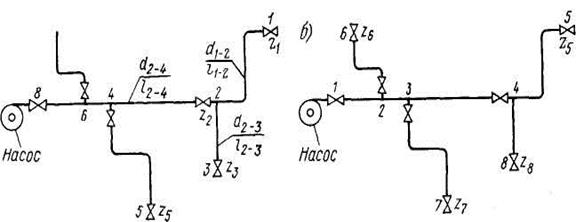
Рис. 36. Расчетные схемы сложного трубопровода:
а — к решению задачи с определением напора и расхода среды;
б — к решению задачи при известных параметрах среды
подачу и напор гидравлического механизма, предназначенного для обслуживания проектируемой системы. Во втором случае находят диаметр трубопровода и параметры движения жидкости в нем, исходя из располагаемого напора системы.
При расчете трубопроводов систем пользуются различными методами. Наибольшее применение получили аналитический метод, метод потерянного напора на единицу длины трубопровода и метод характеристик. Независимо от выбранного метода расчет трубопровода начинают с вычерчивания расчетной схемы и нанесения на нее механизмов, обслуживающих систему, и арматуры (рис. 35 и 36). Трубопровод разбивают на отдельные участки (простые трубопроводы), в пределах которых значения расходов и внутренние диаметры труб постоянны. Участки обычно обозначают двумя цифрами: 1—2, 2—3 и т. д.. первая из которых указывает начало, а вторая — конец участка по ходу расчета. Около каждого участка на выносной линии показывают диаметр трубы и длину участка, а иногда расход и скорость протекающей среды. Кроме того, на схему наносят значения возвышения zi узловых расчетных точек над плоскостью сравнения.
АНАЛИТИЧЕСКИЙ МЕТОД
Данный метод основан непосредственно на решении двух уравнений: уравнения Бернулли и уравнения расхода. Этим методом рассчитывают как простые, так и сложные (разветвленные) трубопроводы.
Расчет простого трубопровода. В расчетной схеме сеть трубопроводов системы обычно разбивают на отдельные участки, в пределах которых сохраняются постоянство расхода жидкости и постоянство диаметра сечения трубы. Такие трубопроводы называют простыми.
Рассмотрим расчет простого трубопровода (см. рис. 35). Напишем уравнение Бернулли для сечений 1 и 2 трубопровода:
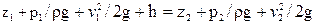 (23)
(23)
Входящая в уравнение величина h, представляющая собой потери на трение и местные сопротивления, определяется зависимостью
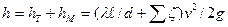 (24)
(24)
Подставив в уравнение (23) значение h по формуле (24) и решив его относительно p2/rg, получим напор H2 в узловой точке 2:
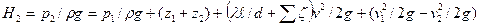 (25)
(25)
Так как диаметр трубопровода постоянный, то 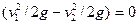 и уравнение (25) примет окончательный вид
и уравнение (25) примет окончательный вид
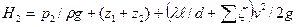
Представим зависимость (24) в виде
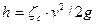 (26)
(26)
где 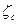 — суммарный (полный) коэффициент сопротивления трубопровода системы, определяемый по формуле
— суммарный (полный) коэффициент сопротивления трубопровода системы, определяемый по формуле
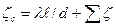 (27)
(27)
Поскольку в основной расчётной формуле (26) потери напора выражены в функции скоростного напора, то рассматриваемый метод расчёта часто называют методом динамических напоров.
Из формулы (26) получим выражение для скорости движения жидкости в трубопроводе
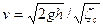
Расход жидкости в трубопроводе будет равен расходу жидкости у потребителя в точке 1. Для большинства потребителей (пожарного ствола, водораспылителя, дренчера и др.)
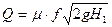 (28)
(28)
где 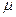 — коэффициент расхода;
— коэффициент расхода;
f — площадь сечения отверстия истечения у потребителя, м2;
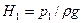 — напор у потребителя, м.
— напор у потребителя, м.
Зная расход Q, можно найти диаметр трубопровода по формуле
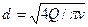 (29)
(29)
Покажем, как используют формулы при расчете трубопроводов. Если напор H2 в узловой точке 2 (см. рис. 35) является искомой величиной, то расчет трубопровода выполняют в такой последовательности: исходя из заданного напора Н1 у потребителя определяют расход Q жидкости по формуле (28); задавшись скоростью движения жидкости в трубопроводе, вычисляют его диаметр d по формуле (29); подбирают условный проход трубы, а затем находят по соответствующему государственному стандарту фактические наружный и внутренний диаметры трубы; уточняют скорость движения жидкости в трубе по формуле υ 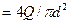 ; вычисляют число Рейнольдса
; вычисляют число Рейнольдса 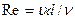 ; по найденному значению Re и принятому значению эквивалентной шероховатости kэ вычисляют коэффициент гидравлического трения l или находят его по графику рис. 31; пользуясь табл. 4 или другими источниками, определяют сумму коэффициентов местных сопротивлений
; по найденному значению Re и принятому значению эквивалентной шероховатости kэ вычисляют коэффициент гидравлического трения l или находят его по графику рис. 31; пользуясь табл. 4 или другими источниками, определяют сумму коэффициентов местных сопротивлений 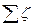 ; вычисляют суммарный коэффициент сопротивлений
; вычисляют суммарный коэффициент сопротивлений 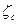 по формуле (27); определяют потери напора h в трубопроводе по формуле (26); находят напор в узловой точке 2 по выражению H2=H1+h+(z1-z2). Из данного расчета видно, что задача решается полностью и в конечном виде.
по формуле (27); определяют потери напора h в трубопроводе по формуле (26); находят напор в узловой точке 2 по выражению H2=H1+h+(z1-z2). Из данного расчета видно, что задача решается полностью и в конечном виде.
Рассмотрим случай гидравлического расчета того же трубопровода 1—2, когда напор H2 в узловой точке 2 является заданным. Цель расчета — определить скорость v жидкости в трубопроводе, а также расход Q и напор H1 ее у потребителя. Диаметр d трубопровода предварительно назначают. Данная задача решается рядом последовательных приближений. Задаемся в 1-м приближении напором у потребителя H1=H1’ и вычисляем следующие величины:
расход воды на участке
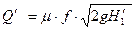 ;
;
скорость движения жидкости в трубопроводе
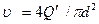 ;
;
число Рейнольдса
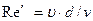
суммарный коэффициент сопротивления трубопровода
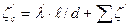
потери напора в трубопроводе
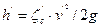
Далее решаем задачу во 2-м приближении. Напор у потребителя будет равен
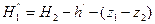
Повторяем расчет по тем же формулам и в такой же последовательности, как и в 1-м приближении. В результате получаем 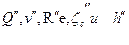 . И так делаем ряд последовательных приближений, пока не получим значения напора
. И так делаем ряд последовательных приближений, пока не получим значения напора 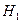 для всех двух последующих приближений, близкие между собой.
для всех двух последующих приближений, близкие между собой.
Расчет сложного трубопровода. Любой сложный (разветвленный) трубопровод состоит из отдельных простых трубопроводов, соединенных по определенной схеме. Гидравлический расчет разветвленного трубопровода (см. рис. 36) выполняется по участкам и обычно сводится к применению для них решений, рассмотренных для простых трубопроводов. Как видно из рис. 36, насос по разветвленному трубопроводу подает воду к целому ряду потребителей. В данной схеме число потребителей равно четырем; в общем случае их может быть значительно больше. Предположим, что напор H и подача Q насоса неизвестны. Расчет трубопровода производим последовательно по участкам от самой отдаленной точки 1 к насосу (рис. 36, а). Участок /—2 представляет собой простой трубопровод и рассчитывается в таком порядке:
расход воды на участке
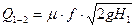
диаметр трубопровода
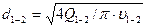 ,
,
где 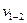 — скорость жидкости в трубопроводе, которой задаются в предела 2-4 м/с,
— скорость жидкости в трубопроводе, которой задаются в предела 2-4 м/с,
число Рейнольдса
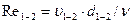
суммарный коэффициент сопротивления трубопровода
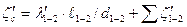 ;
;
потери напора на участке
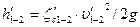
напор в точке 2
Участок 2—3 также представляет собой простой трубопровод, и поскольку для него напор в точке 2 тот же, что и для участка , то рассчитывают его рядом последовательных приближений.
Участок 2—4 — простой трубопровод и рассчитывается следующим образом. Определяют расход воды на участке а затем вычисляют и находят напор Я4 в точке 4 по формуле
После этого рассчитывают участки 4—5, 4—6, 6—7 и 6—5.
Подача и напор насоса системы будут равны:
В общем случае потребную подачу насоса определяют по выражению
где — сумма расходов воды потребителями, работающими одновременно.
Из всех возможных комбинаций одновременной работы потребителей берут тот случай, когда расход воды будет максимальным.
Если подача Q и напор Я насоса заданы, то целью расчета является определение параметров движения жидкости по участкам, а также напора и расхода жидкости у потребителей. На участки трубопровод разбивают в направлении от насоса к самой удаленной точке (рис. 36, 6). Расчет начинают с магистрали 14, а затем рассчитывают отдельные ответвления. Приняв скорость движения жидкости в магистрали равной 2-4 м/с, определяют ее диаметр по формуле
Участки магистрали рассчитывают последовательно один за другим, начиная с участка /—2. Для этого участка имеем:
число Рейнольдса
потери напора
напор в точке 2
Аналогично рассчитывают участки 2—3 и 3—4.
Напор в точке 3
Напор в точке 4
По известным напорам в узловых точках 2,3 и 4 рассчитывают ответвления 2—6, 3—7, 4—8 и 4—5.
Дата добавления: 2015-12-11; просмотров: 1343;
