Свойства смешанного произведения
1. Смешанное произведение не изменяется:
а). Если перемножаемые вектора переставлять в круговом порядке:
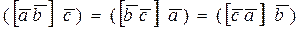
б). Если поменять местами знаки векторного и скалярного умножения:
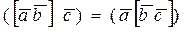
Это позволяет записывать смешанное произведение трех векторов в виде 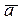
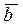
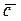 без знаков векторного и скалярного умножения.
без знаков векторного и скалярного умножения.
2. Перестановка в смешанном произведении любых двух векторов изменяет лишь его знак:
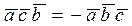 ,
, 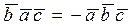 ,
, 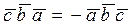 .
.
Действительно, используя равенства
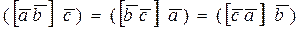 ;
; 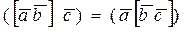
имеем:
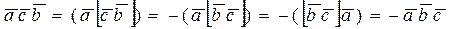
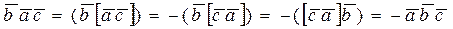
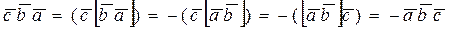
3. Смешанное произведение обращается в нуль, если:
а). Хотя бы один из перемножаемых векторов ест нуль - вектор,
б). Два из перемножаемых векторов коллинеарны,
в). Три перемножаемых вектора компланарны.
Координатная форма записи смешанного произведения
Коротко смешанное произведение записывается в виде определителя третьего порядка:
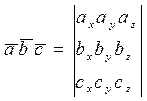 (1.8.2.1)
(1.8.2.1)
Замечание 1.При помощи смешанного произведения можно вычислить объем четырехгранной пирамиды, заданной координатами ее вершин:
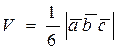
Замечание 2.Три вектора 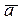 ,
, 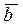 ,
, 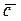 компланарны тогда и только тогда, когда их смешанное произведение равно 0.
компланарны тогда и только тогда, когда их смешанное произведение равно 0.
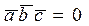 или
или 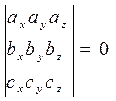
Дата добавления: 2015-12-10; просмотров: 747;
