Электронно-дырочный переход в состоянии равновесия

Принцип действия большинства полупроводниковых приборов основан на физических явлениях, происходящих в области контакта твердых тел. При этом преимущест­венно используются контакты: полупроводник-полупровод­ник; металл-полупроводник; металл-диэлектрик-полупро­водник.

Если переход создается между полупроводниками n-типа и p-типа, то его называют электронно-дырочным или p-n переходом.

Электронно-дырочный переход создается в одном кри­сталле полупроводника с использованием сложных и раз­нообразных технологических операций.

Рассмотрим p-n переход, в котором концентрации до­норов N_д и акцепторов N_a изменяются скачком на границе раздела (рис. 1.7, а). Такой p-nпереход называют рез­ким. Равновесная концентрация дырок в p-области ( 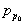) значительно превышает их концентрацию в n-области ( 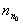). Аналогично для электронов выполняется условие 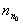> 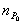. Неравномерное распределение концентраций одноименных носителей зарядов в кристалле (рис. 1.7, б) приводит к возникновению диффузии электронов из n-области в p-область и дырок из p-области в n-область. Такое движе­ние зарядов создает диффузионный ток электронов и ды­рок. С учетом выражений (1.13) и (1.14) плотность полно­го диффузионного тока, проходящего через границу разде­ла, определится суммой

.

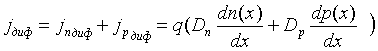Электроны и дырки, переходя через контакт навстречу друг другу (благодаря диффузии), рекомбинируют и в приконтактной области дырочно­го полупроводника образуется нескомпенсированный заряд отрицатель­ных ионов акцепторных примесей, а в электронном полу­проводнике нескомпенсирован -ный заряд положительных донорных ионов (рис. 1.6, в). Таким образом, электрон­ный полупроводник заряжается положительно, а дыроч­ный - отрицательно. Между областями с различными ти­пами электропроводности возникает собственное электри­ческое поле напряженностью E_соб (рис. 1.7, а), созданное двумя слоями объемных зарядов.

Этому полю соответствует разность потенциалов U_к между n- и p-областями, назы­ваемая контактной (рис. 1.7, г). За пределами области объемного заряда полупроводниковые области n- и р-типа остаются электрически нейтральными.

Собственное электрическое поле является тормозя­щим для основных носителей заряда и ускоряющим для неосновных. Электроны p-области и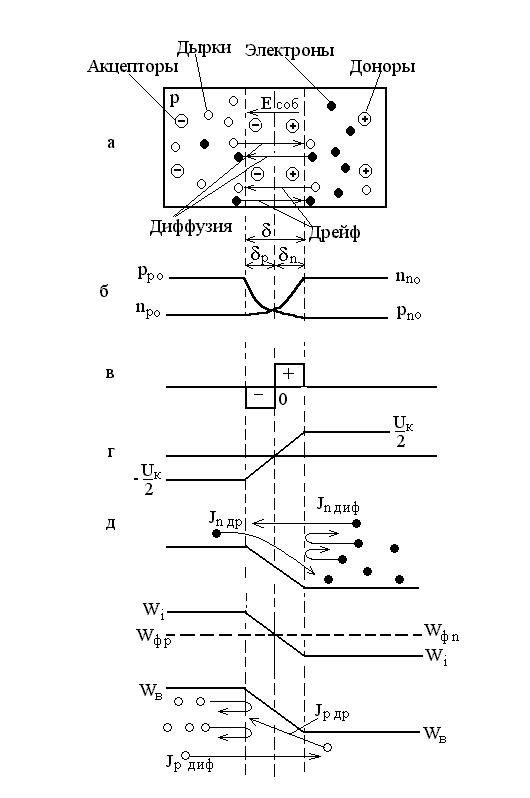

Рисунок 1.7 Равновесное состояние p-n перехода.

дырки n-области, со­вершая тепловое движение, попадают в пределы диффузи­онного электрического поля, увлекаются им и перебрасы­ваются в противоположные области, образуя ток дрейфа, или ток проводимости.

Выведение носителей заряда из области полупроводни­ка, где они являются неосновными, через электронно-дырочный переход ускоряющим электрическим полем назы­вают экстракцией носителей заряда.

Используя выражение (1.12) и учитывая, что Е = -dU/dx, определяем плотность полного дрейфового тока через гра­ницу раздела p- и n-областей:

.

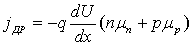Так как через изолированный полупроводник ток про­ходить не должен, между диффузионным и дрейфовым то­ками устанавливается динамическое равновесие:

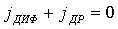. (1.15)

Приконтактную область, где имеется собственное электрическое поле, называют p-n переходом.

Поскольку потенциальная энергия электрона и потен­циал связаны соотношением W = -qU, образование не­скомпенсированных объемных зарядов вызывает пониже­ние энергетических уровней n-области и повышение энер­гетических уровней р-области. Смещение энергетических диаграмм прекратится, когда уровни Ферми W _фn и W _фp совпадут (рис. 1.7, д). При этом на границе раздела (x = 0) уровень Ферми проходит через середину запрещенной зоны. Это означает, что в плоскости сечения x = 0 полупровод­ник характеризуется собственной электропроводностью и обладает по сравнению с остальным объемом повышен­ным сопротивлением. В связи с этим его называют запи­рающим слоем или областью объемного заряда.

Совпадение уровней Ферми n- и p-областей соответству­ет установлению динамического равновесия между облас­тями и возникновению между ними потенциального барь­ера U_k для диффузионного перемещения через p-n переход электронов n-области и дырок p-области.

Из рис. 1.7, д следует, что потенциальный барьер

.

Подстановка в это выражение результатов логарифмиро­вания соотношений (1.4), (1.7) позволяет получить сле­дующее равенство:

.

Если обозначить j_т = kT/q и учесть уравнение (1.10), то можно записать:

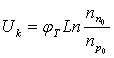; (1.16) 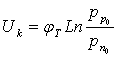. (1.17)

Из уравнений (1.16) и (1.17) следует:

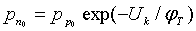; . (1.18)

При комнатной температуре (Т = 300 К) j_т > 0,026 В.

Таким образом, контактная разность потенциалов зави­сит от отношения концентраций носителей зарядов одного знака в р- и n-областях полупроводника.

Другим важным параметром p-n перехода является его ширина, обозначаемая d = d_p + d_n.

Ширину запирающего слоя d можно найти, решив урав­нения Пуассона для n-области и p-области:

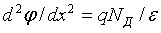; (1.19) 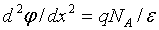. (1.20)

Решения уравнений (1.19) и (1.20) при граничных ус­ловиях

; ;

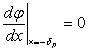
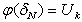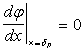
имеют вид:

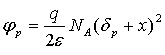для -d_p < x < 0;

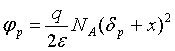для 0 < x <d_n; (1.21)

В точке x = 0 оба решения должны давать одинаковые значения j и 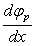. Приравняв 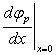и 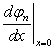, можно записать:

. (1.22)

Из равенства (1.22) видно, что ширина слоев объемных зарядов в n- и p-областях обратно пропорциональна кон­центрациям примесей и в несимметричном переходе запи­рающий слой расширяется в область с меньшей концен­трацией примесей.

На основании равенства (1.22) можно записать:

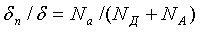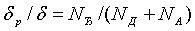; , (1.23)

где d = d_n + d_р.

Приравнивая правые части уравнений (1.21) и учиты­вая соотношения (1.23), при x = 0 получаем

.

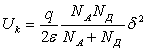На основании этого выражения формулу для определения ширины запирающего слоя p-n перехода можно записать в следующем виде:

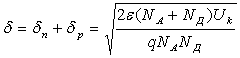. (1.24)

Из соотношения (1.24) видно, что на ширину запираю­щего слоя существенное влияние оказывает концентрация примесных атомов. Увеличение концентрации примесных атомов сужает запирающий слой, а уменьшение расширя­ет его. Это часто используется для придания полупровод­никовым приборам требуемых свойств.