Двойной электрический слой и электрокинетические явления.

В системах цемент-вода, глина-вода и др. силикатных системах протекают электрокинетические явления, которые возникают при относительном перемещение фаз в жидких коллоидных системах, к которым относятся электроосмос, электрофорез, потенциал течения и потенциал оседа­ния.

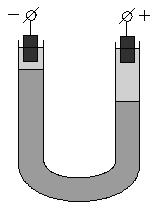
Если поместить золь в постоянное электрическое поле, то, как и в растворах электролитов, заряженные частицы будут двигаться к противоположно заряженным электродам: коллоидная частица с адсорбированными на ней противоионами – в одну сторону, противоионы диффузного слоя – в другую. Движение частиц дисперсной фазы в электрическом поле называется электрофорезом. Явление электрофореза можно наблюдать, поместив в U-образную трубку какой-либо окрашенный золь, поверх которого налит не смешивающийся с золем бесцветный электролит.

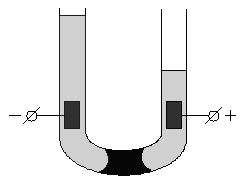
Если опустить в электролит электроды и наложить разность потенциалов, то граница окрашенного золя в одном из колен трубки будет подниматься, в другом – опускаться (рис. 4.13). Если поместить в U-образную трубку пористую перегородку (например, мелкий кварцевый песок) и заполнить её водой, то при наложении разности потенциалов в одном колене будет наблюдаться подъем уровня жидкости, в другом – его опускание (рис. 4.14). Движение дисперсной среды в электрическом поле относительно неподвижной дисперсной фазы (в рассмотренном случае – относительно поверхности пористых тел) называется электроосмосом.

Рис. 4.13 Схема опыта по электрофорезу	Рис. 4.14 Схема опыта по электроосмосу

Скорость движения частиц дисперсной фазы при электрофорезе, а также скорость движения дисперсной среды при электроосмосе прямо пропорциональны напряженности электрического поля E и диэлектрической проницаемости дисперсионной среды ε и обратно пропорциональны вязкости среды η. Скорость движения частиц дисперсной фазы при электрофорезе U связана с величиной ζ-потенциала уравнением Гельмгольца-Смолуховского (К – постоянная, зависящая от формы частиц дисперсной фазы; для сферических частиц К = 6):

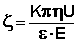(IV.20)

Обратные электрофорезу и электроосмосу электрокинетические явления (т.н. электрокинетические явления второго рода) называются соответственно потенциал седиментации и потенциал протекания. Потенциал седиментации (эффект Дорна) – возникновение разности потенциалов при вынужденном движении дисперсной фазы относительно неподвижной дисперсионной среды (например, под действием силы тяжести). Потенциал протекания (эффект Квинке) есть явление возникновения разности потенциалов при движении дисперсионной среды относительно неподвижной дисперсной фазы (например, при продавливании электролита через пористое тело). Причиной всех этих явлений является возникновение ДЭС на границе раздела фаз.

Модели ДЭС

Первая теория строения ДЭС была развита Гельмгольцем и Перреном; в их представлении двойной электрический слой подобен плоскому конденсатору, внутренняя обкладка которого находится в твердой фазе, а внешняя – в жидкости параллельно поверхности ядра на расстоянии порядка диаметра иона. Потенциал электрического поля внутри ДЭС φ в этом случае линейно уменьшается с увеличением расстояния от поверхности r (рис. 4.12а).

Позднее Гуи и Чепмен предложили другую модель, согласно которой противоионы, благодаря тепловому движению, образуют вблизи твердой поверхности ядра диффузную ионную атмосферу. Уменьшение электрического потенциала ДЭС φ с увеличением расстояния r в этом случае происходит нелинейно (рис. 4.12б).

Предложенная Штерном модель строения ДЭС объединяет ранние модели, учитывая как адсорбцию противоионов, так и их тепловое движение. Согласно этой модели, являющейся в настоящее время общепринятой, часть противоионов находится на расстояниях порядка диаметра иона от поверхности ядра, образуя т.н. слой Гельмгольца (адсорбционный слой противоионов), а другая часть образует диффузный слой (т.н. слой Гуи). Потенциал диффузной части двойного электрического слоя называют электрокинетическим потенциалом (см. рис.4.12в).

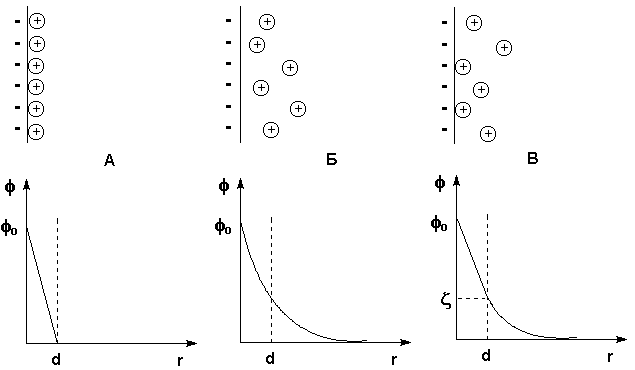
Рис. 4.12 Строение ДЭС: а) – по Гельмгольцу и Перрену, б) – по Гуи и Чепмену, в) – по Штерну. Вверху – схема расположения противоионов, внизу – зависимость потенциала от расстояния.

Экспериментально было установлено, что при движении твердой и жидкой фаз относительно друг друга скольжение жидкости происхо­дит не у твердой поверхности, а в самой жидкости по границе между адсорбционным и диффузным слоями по так называемой поверхности скольжения.

При этом на этой границе создает­ся разность потенциалов, называемая электрокинетическим или дзета-потенциалом (x-потенциал), определяемым как разность по­тенциалов между адсорбционным слоем, неподвижно связанным с поверхностью твердой фазы, и всей остальной (подвижной) массой жидкости. Величина x-потенциала обусловлена толщиной диффузного слоя противоионов. Чем больше значение ξ, тем более устойчива коллоидная системы. При введении в коллоидный раствор электролитов диффузионный слой будет сжиматься и все большее число противоионов будет попадать в адсорбционный слой, умень­шая x-потенциал и постепенно приближая его значение к нулю (изо-электрическое состояние коллоида). В этом состоянии электрокинетические явления отсутствуют.

Седиментация

Частицы дисперсной фазы одновременно испытывают действие силы земного притяжения и архимедовой силы; в зависимости от соотношения плотностей дисперсионной среды и дисперсной фазы равнодействующая этих сил будет вынуждать частицы к оседанию либо всплытию. Процесс оседания либо всплытия коллоидных частиц в золе называется седиментацией. Однако седиментации всегда противодействует другой процесс, стремящийся к равномерному распределению коллоидных частиц по всему объему раствора – диффузия, осуществляемая под действием броуновского движения частиц. Соотношение между этими двумя процессами определяет кинетическую устойчивость золей – способность коллоидных частиц удерживаться во взвешенном состоянии, не подвергаясь седиментации.

В статистической теории броуновского движения, развитой А. Эйнштейном, вводится понятие средний сдвиг ±Δx, представляющий собой проекцию расстояния между положениями частицы X₁ и X₂, в которых частица находилась во время двух последовательных наблюдений через время t. Значение квадрата среднего сдвига можно найти по уравнению Эйнштейна, связывающего Δx² с температурой T, радиусом взвешенных частиц r и вязкостью среды η:

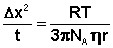(IV.21)

Средний сдвиг частицы связан с коэффициентом диффузии D, который может быть рассчитан по уравнению (IV.22):

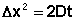(IV.22)

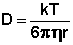(IV.23)

Как видно из уравнения (IV.23), величина коэффициента диффузии определяется отношением тепловой энергии молекул kT и вязкостного сопротивления диффузии со стороны среды. Поскольку процесс диффузии проявляется тем сильнее, чем меньше масса коллоидных частиц, более крупные частицы оседают либо всплывают в первую очередь. Кинетическая устойчивость золя, таким образом, прямо пропорциональна степени дисперсности золя. Заметное оседание частиц в системе, обладающей высокой кинетической устойчивостью, можно вызвать при помощи центрифугирования золя, используя значительные по величине центробежные силы, что многократно увеличивает силу, действующую на частицу и способствующую её оседанию (современные ультрацентрифуги работают при ускорениях свыше 400000g).

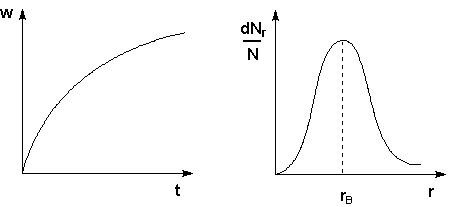
Рис. 4.15 Кривая седиментации Рис. 4.16 Кривая распределения

Методы седиментации и ультрацентрифугирования применяются для изучения полидисперсности коллоидных систем, обусловленной существованием в коллоидных системах частиц различных размеров. Изучение полидисперсности коллоидных систем для установления количественного распределения частиц по размерам (т.н. кривых распределения) – седиментационный анализ – производится при помощи измерения возрастания веса осевших частиц w со временем. По результатам такого исследования строят кривые седиментации (рис. 4.15). Проводя анализ кривой седиментации, можно рассчитать кривую распределения для данной системы, которая характеризует относительное содержание в системе частиц разного размера (рис. 4.16). Обычно кривые распределения содержат один максимум, который соответствует r_в – наиболее вероятному радиусу частиц дисперсной фазы.