Емкость канала связи

Скорость передачи информации, а ее предельно допустимое значение для данного канала называют емкостью канала, относится к фундаментальным понятиям теории связи. Она служит одной из главных характеристик канала передачи информации. Оценка скорости передачи информации и предельных возможностей канала связи представляет большой практический и теоретический интерес.

Рассматривая процесс передачи информации в общих чертах, можно предположить, что основными факторами, ограничивающими скорость передачи информации, являются полоса пропускания и уровень помех.

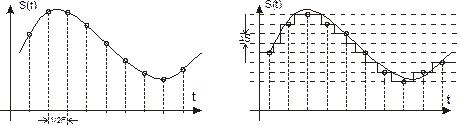
Существует фундаментальная теорема о „выборках«, которая доказывает, что сигнал, не содержащий в своем спектре частот выше , может представляться 2 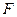независимыми значениями в секунду, и совокупность значений, отстоящих друг от друга на Т секунд, определяет непрерывный сигнал полностью. Заметим, что „выборкой« является отсчет амплитуды сигнала в определенный момент (на рис. 5.12 а можно увидеть эти выборки).

а) б)

Рис. 5.12. Представление непрерывного сигнала в виде дискретных отсчетов (выборок);

а — отсчеты сигнала, взятые через интервал 1 /(2F); б — отсчеты сигнала, квантованные по амплитуде.

Термин „выборки« взят от английского samples, теорему о выборках называют также теоремой отсчетов.

Эта теорема позволяет на интервале Т заменить непрерывный сигнал с ограниченным спектром последовательностью его дискретных значений, причем их нужно не бесконечное число, а вполне определенное, равное . Уровень шумов (помех) не позволяет точно определить амплитуду сигнала и в этом смысле вносит некоторую неопределенность в значение отсчетов сигнала.

Максимально возможная скорость передачи информации по каналу связи при фиксированных ограничениях называется емкостью канала, обозначается через С и имеет размерность бит/с.

Рассмотрим соотношение для емкости канала связи, являющееся фундаментальным соотношением в теории связи. Оно позволяет понять некоторые принципиальные зависимости при передаче информации вообще.

Напомним, что количество информации I, снимающее неопределенность о состоянии объекта с L равновероятными состояниями,

.

Основание логарифма здесь не имеет значения. Если основание равно двум, то единицей измерения количества информации оказывается бит.

Определим количество различных сообщений, которое можно составить из п элементов, принимающих любые из т различных фиксированных состояний. Из ансамбля п элементов, каждый из которых может находиться в одном из т фиксированных состояний, можно составить 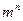различных комбинаций, т. е. 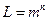. Тогда

= .

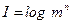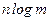При полосе F наибольшее число отсчетов сигнала равно 2F в единицу времени или 2FТ за время Т, то есть n = 2FT.

Если бы шума не существовало, то число дискретных уровней сигнала было бы бесконечным. В случае наличия шума последний определяет степень различимости отдельных уровней амплитуды сигнала. Так как мощность является усредненной характеристикой амплитуды, число различимых уровней сигнала по мощности равно (Р_с+Р_ш)/Р_ш), а по амп­литуде соответственно .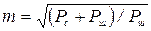

Тогда ёмкость канала

.

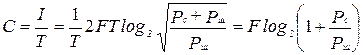Итак, емкость канала ограничивается двумя величинами: шириной полосы канала и шумом. Приведенное соотношение известно как формула Хартли-Шеннона и считается основной в теории информации.

Полоса частот и мощность сигнала входят в формулу таким образом, что для С = const при сужении полосы необходимо увеличивать мощность сигнала, и наоборот.

Емкость канала является максимальной величиной скорости. Чтобы достигнуть такой скорости передачи, информация должна быть закодирована наиболее эффективным образом. Утверждение, что такое кодирование возможно, является важнейшим результатом созданной Шенноном теории информации . Шеннон доказал принципиальную возможность такого эффективного кодирования, не определив, однако, конкретных путей его реализации. (Отметим, что на практике инженеры часто говорят о ёмкости канала, подразумевая под этим реальную, а не потенциальную скорость передачи).

Рис. 5.13 Эффективность цифровых систем связи: 1-граница Шеннона; 2- М-ичная ФМ; 3-М-ичная АМ; 4- М-ичная ЧМ.

Эффективность систем связи характеризуется параметром, равным скорости передачи информации R на единицу ширины полосы F, т. е. R/F. Для иллюстрации существующих возможностей по созданию эффективных систем связи на рис. 5.13 приведены графики зависимости эффективности передачи информации при различных видах М-ичной дискретной амплитудной, частотной и фазовой модуляции (кроме бинарной модуляции используется также модуляция с 4, 8, 16 и даже с 32 положениями модулируемого параметра) от отношения энергии одного бита к спектральной плотности мощности шума (Ео/Nо). Для сравнения показана также граница Шеннона.

Сравнение кривых показывает, в частности, что при неизменном отношении сигнал-шум наиболее популярный вид модуляции 4ФМн в три раза хуже потенциально достижимого. Из сравнения кривых можно сделать более общие выводы: наиболее эффективной оказывается передача с фазовой дискретной модуляцией; современные методы кодирования и модуляции еще весьма далеки от совершенства.