Регулирование теплообменников смешения.
Регулирование теплообменников смеше-F1
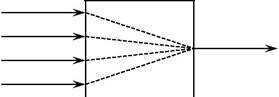
| ниязаключается в поддержании постоянства тем- | F2 | Tсм | ||
| пературы Тсм суммарного потока на выходе. Для | T1 | |||
| создания необходимого температурного режима в | T2 | |||
| химических аппаратах используют передачу энер- | ||||
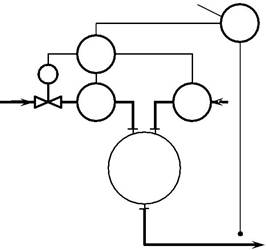
| Рис. 5.1.Структурная схема регулиро- | ||||
| гии в результате смешения двух и более веществ с | вания теплообменника смешения. | |||
| разными теплосодержаниями. |
Во многих задачах регулирования состава или температуры в резервуаре с мешалкой при определении передаточных функций принимают перемешивание идеальным. Тогда объ-ект описывается дифференциальным уравнением первого порядка с постоянной времени, рав-ной времени пребывания в резервуаре. Однако на практике отмечается запаздывание, по исте-чении которого изменение концентрации или температуры питания происходит на выходе из резервуара. Это запаздывание (запаздывание смешения) зависит от размеров резервуара, вяз-кости жидкости, конструкции и скорости вращения мешалки, определяющих интенсивность
| перемешивания. | |||||
| Если | T2> Tсм > T1,при этом теплоемкости и плотности жидкостей одинаковы,то | ||||
| Tсм = T1+ | F2 | (T2 | −T1 ) , (потерями в окружающую среду пренебрегаем) | ||
| F1 | + F2 | ||||
Остановимся на особенностях статической характеристики собственно процесса сме-шения. Рассмотрим для примера аппарат непрерывного действия, в котором смешиваются два потока с расходами G1 и G2, температурами θ1 и θ2, удельными теплоёмкостями cp1 и cp2 (рис. 5.2).
Пусть задача регулирования состоит в поддержании заданного значения θ0 температу-ры выходного потока путём изменения расхода G1 при условии, что основными источниками возмущений являются расход и температура второго потока G2 и θ2, а температура θ1 и удель-
ные теплоёмкости веществ постоянны и равны θ10 , c p1 и c p 2 . Найдем статические характери-
стики объекта по каналу регулирования G1 −θ и каналам возмущения G2 −θ и θ2 −θ (рис. 5.3). Для этого запишем уравнение теплового баланса:
| G θ 0 c | p1 | + G θ | c | p 2 | = (G + G | )θc | p | , | |||||||||||||||||||||||||||||||||||||
| 1 1 | 2 2 | ||||||||||||||||||||||||||||||||||||||||||||
| где c | p | = (G c | p1 | +G | c | p2 | ) /(G +G | ) . | |||||||||||||||||||||||||||||||||||||
| Отсюда | |||||||||||||||||||||||||||||||||||||||||||||
| G θ 0 c | p1 | G θ | c | p 2 | |||||||||||||||||||||||||||||||||||||||||
| θ = | + | . | (5.1) | ||||||||||||||||||||||||||||||||||||||||||
| G c | p1 | +G | c | p 2 | G c | p1 | + G | c | p 2 | ||||||||||||||||||||||||||||||||||||
| Как видно из (5.1), характерной | G1,θ1, c p1 | G2,θ2, c p2 | |||||||||||||||||||||||||||||||||||||||||||
| особенностью | теплообменников | сме- | |||||||||||||||||||||||||||||||||||||||||||
| шения является нелинейность стати- | |||||||||||||||||||||||||||||||||||||||||||||
| ческих характеристик по температур- | G1+ G2,θ, c p | ||||||||||||||||||||||||||||||||||||||||||||
| ным каналам, θ1 – θ и θ2 – θ . | Рис. 5.2.Принципиальная схема теплообменника | ||||||||||||||||||||||||||||||||||||||||||||
| При условии малых отклонений | |||||||||||||||||||||||||||||||||||||||||||||
| смешения. |
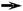

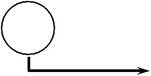
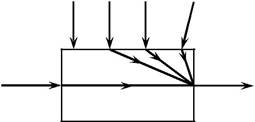
| координат объекта от их заданных | θ1 | G2 | θ2 | z | ||
| значений можно провести линеариза- | ||||||
| цию зависимости (5.1) и найти при- | G1 | θ | ||||
| ближенно | коэффициенты | усиления | ||||
| объекта по каждому каналу. | Рис. 5.3.Структурная схема теплообменника сме- | ||||||||||||||||||||||||||||||||||||||||
| Обозначим | заданные | значения | шения. | ||||||||||||||||||||||||||||||||||||||
| входных и выходных координат через G0 | , | G 0, | θ | и разложим функцию (5.1) в ряд Тейлора в | |||||||||||||||||||||||||||||||||||||
| малой окрестности G0 , | G0, θ 0: | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| ∂θ | ∂θ | 0 | ∂θ | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||
| θ =θ | + | (G1 −G1 | ) + | ∂G | (G2 | −G2 | ∂θ | (θ2 −θ2 ) | , | |||||||||||||||||||||||||||||||||||||||||||||
| ∂G | ) + | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| где | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ∂θ | G20 c p1c p 2(θ10−θ20) | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ∂G | (G 0 c | + G 0 c | )2 ; | |||||||||||||||||||||||||||||||||||||||||||||||||||
| p1 | p 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| ∂θ | 0 | G10 c p1c p 2(θ20−θ10) | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ∂G | (G 0 c | + G 0 c | )2 | ; | (5.2) | |||||||||||||||||||||||||||||||||||||||||||||||||
| p1 | p 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| ∂θ | 0 | G20 c p 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ∂θ | G 0 c | + G | 0 c | . | ||||||||||||||||||||||||||||||||||||||||||||||||||
| p1 | p 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| Переходя к отклонениям y =θ −θ 0 , | x | р | = G −G 0 | , | x | в1 | = G | −G 0 , | x | в2 | =θ | −θ 0 | , получим урав- | |||||||||||||||||||||||||||||||||||||||||
| нение статической характеристики в виде: | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| y = k р x р + k1 xв1+ k2 xв2, | (5.3) | |||||||||||||||||||||||||||||||||||||||||||||||||||||
| ∂θ | 0 | ∂θ | 0 | ∂θ | ||||||||||||||||||||||||||||||||||||||||||||||||||
| где | k | р = | ; | |||||||||||||||||||||||||||||||||||||||||||||||||||
| ∂G | ∂G | ∂θ | ||||||||||||||||||||||||||||||||||||||||||||||||||||
| ; | k1 = | k2 = | . | |||||||||||||||||||||||||||||||||||||||||||||||||||
Анализ зависимостей (5.3) показывает, что даже при обычных возмущениях, наблю-даемых на практике, ошибка в результате линеаризации может оказаться существенной. На-
пример, при увеличении расхода G2 на 30 % по сравнению с заданным коэффициент усиления
| kр может изменится на5-20%, а k1 | – на 25-40% от расчетных, в зависимости от соотношения | ||||||||||||||||||||||||
| расходов G1 и G2. Стабилизация отношения G / G | = γ 0 | позволяет уменьшить влияние этой | |||||||||||||||||||||||
| нелинейности, так как | |||||||||||||||||||||||||
| θ | 0 c | р1 | θ 0 c | р2 | θ 0 c | р1 | θ 0 c | р2 | |||||||||||||||||
| θ = | + | = | + | ||||||||||||||||||||||
| G2 | G2 | γ 0 c р1+ c р2 | |||||||||||||||||||||||
| c р1+ | G | c р2 | G | c р1 | + c р2 | c р1+ | γ 0 | c р2 | |||||||||||||||||
и при отсутствии других возмущений, кроме G2, будет обеспечиваться постоянство выходной температуры.
Наличие других источников возмущения, кроме G2, потребует введение коррекции γ 0 ,
например, в зависимости от значения выходной температуры θ (см. пример каскадной АСР,
рис. 5.7).
Рассмотрим насколько вариантов систем автоматизации теплообменников смешения и проведем их сравнительный анализ по качеству процессов регулирования.
Вариант1. Задача стабилизации выходной температуры смеси θ решается применени-ем одноконтурной замкнутой системы регулирования, в котором регулирующим воздействи-
ем является расход G1 (рис. 5.4). Использование регулятора с интегральной составляющей и законе регулирования (ПИ- или ПИД-регулятор) гарантирует поддержание заданного значе-ния θ в установившемся режиме, однако качество переходного процесса может оказаться не-удовлетворительным при большой инерционности канала регулирования и сильных возмуще-ниях.
| G1 | G2 | θ1 | G2 | θ2 | z | |
| G1 | θ | |||||
| Объект | ||||||
| TC | θ | Регулятор | θ 0 | |||
| а | ||||||
| б |
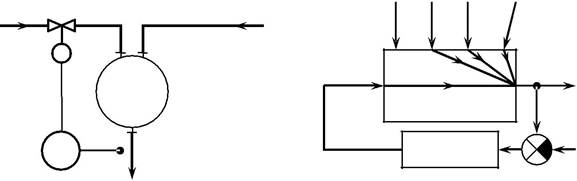
Рис. 5.4.Функциональная(а)и структурная(б)схемы замкнутой одноконтурной АСР темпе-ратуры в теплообменнике смешения.
Вариант2 включает систему регулирования соотношения расходов G1 и G2 (рис. 5.5). Это разомкнутая система регулирования, способность обеспечить инвариантность регулируе-
мой температуры смеси θ к возмущениям по расходу G2 , однако при наличии любого друго-
го возмущения θ не будет равна заданной.
Вариант3 (рис. 5,6) отличается компенсатором возмущения по θ2 .Таким образом, дан-
ная система регулирования может обеспечить независимость выходной температуры от двух
основных возмущений G2 и θ2 . Однако при наличие других возмущений (например, измене-
ние теплопотерь в окружающую среду) температура будет отклоняться от заданной.
Варианты4и5 являются разновидностями комбинированных АСР, в которых обеспе-чивается компенсация основных возмущений и вводится обратная связь по регулируемой ко-ординате.
FFC
| G1 | FE | FE G2 |
Регулятор
γ 0
R
G1
G2 z
θ
Объект
θ
а б
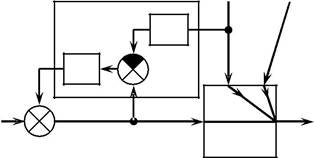
Рис. 5.5.Функциональная(а)и структурная(б)схемы разомкнутой одноконтурной АСР тем-пературы в теплообменнике смешения.
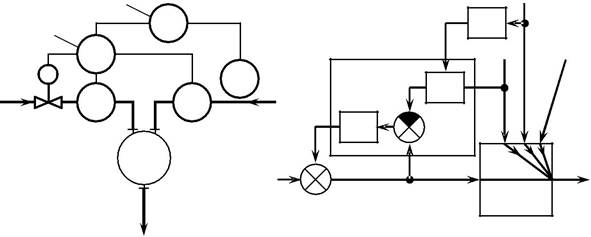
Вариант4 – система регулирования соотношения расходов G1 и G2 с коррекцией ко-
эффициента по выходной температуре смеси θ (рис. 5,7), т.е. двухкаскадная АСР. Основным (внешним) регулятором является регулятор температуры 1, а вспомогательным (внутренним)
– регулятор соотношения 2, осуществляющий компенсацию возмущения по расходу G2 .
| 2 | Компенсатор | ||||||
| θ2 | |||||||
| FFY | |||||||
| 1 | Rk | ||||||
| FFC | |||||||
| TE | Регулятор | G2 | z | ||||
| G1 | FE | FE | ,θ2 | γ 0 | |||
| G2 | R | ||||||
| θ | |||||||
| θ | G1 | Объект | |||||
 а б
а б
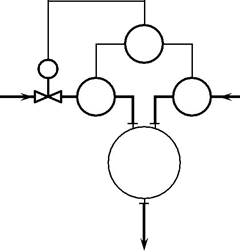
Рис. 5.6.Функциональная(а)и структурная(б)схемы разомкнутой АСР температуры в теп-лообменнике смешения с компенсацией двух возмущений:
1 –регулятор соотношения; 2 –компенсатор.
Вариант5 – система регулирования температуры смеси с коррекцией по двум возму-
щениям G2 и θ2 , т.е. комбинированная АСР. Динамический компенсатор 2 (рис. 5,8) в данном случае должен содержать вычислительное устройство для расчёта корректирующей поправки
на задание по выходной температуре регулятору 1 в зависимости от температуры и расхода второго потока.
2
 FFC
FFC
G1 FE
а
Дата добавления: 2015-11-06; просмотров: 2229;
