Основные соотношения для фазированных АР.

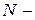Для описания характеристик элементной антенной решетки могут быть использованы соотношения, полученные для линейного излучателя. При этом возбуждение излучателей при остронаправленном излучении обеспечивает синфазное сложение полей в заданном направлении ( 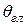, 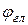), зависящее от положения излучателей ( 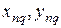, 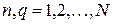) в решетке:

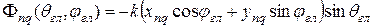. (8.1)

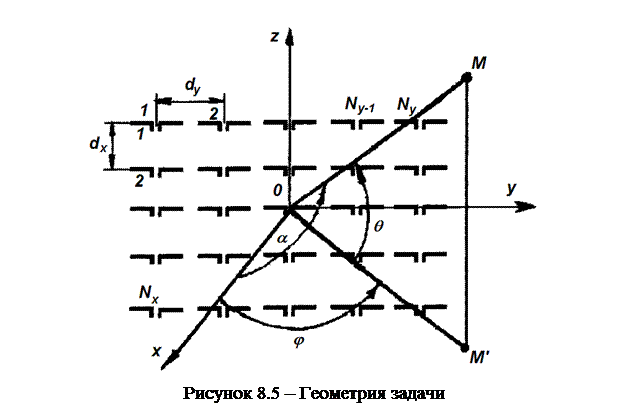
Отсчет углов показан на рисунке 8.5.

Полагая решетку состоящей из одинаковых излучателей, можно представить ее характеристику направленности 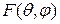в виде произведения парциальной характеристики направленности изолированного излучателя 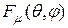и множителя решетки :

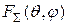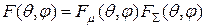. (8.2)

Для ФАР множитель решетки определяется соотношением

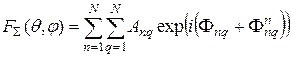, (8.3)

где 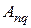‑ амплитуда возбуждения 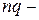го элемента решетки;

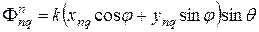‑ пространственный фазовый сдвиг для направления на точку наблюдения ( ).

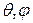При размещении излучателей в узлах координатной сетки с двойной периодичностью синфазное сложение полей отдельных излучателей решетки возможно не только в направлении главного максимума ДН, но и в других направлениях, которым соответствует пространственный фазовый сдвиг, компенсирующий сдвиг фазы между излучателями за счет возбуждения. В этом случае помимо главного максимума существуют еще и дифракционные лепестки высших порядков, пространственная ориентация которых зависит от расстояния между излучателями. При уменьшении этого расстояния число дифракционных максимумов, находящихся в области действительных углов, уменьшается. Для нормальной работы решетки необходимо, чтобы в области действительных углов находился лишь один главный максимум, а дифракционные лепестки отсутствовали.

При использовании прямоугольной сетки дифракционные максимумы высших порядков отсутствуют, если расстояние между излучателями в направлении координатных осей удовлетворяет следующим условиям:

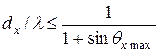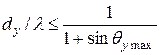, , (8.4)

где 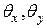‑ максимальные углы отклонения луча в плоскостях 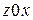и .

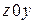Для треугольной сетки соответствующее условие имеет вид:

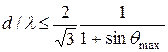. (8.5)

Условия (8.4) и (8.5) не учитывают направленных свойств излучателей решетки и определяют предельные расстояния в решетке изотропных излучателей. При ограниченном секторе сканирования использование направленных излучателей позволяет увеличить расстояние между ними и соответственно уменьшить общее число излучателей.

При сканировании в коническом секторе углов 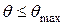выигрыш в числе излучателей по сравнению с решеткой изотропных излучателей для треугольной и прямоугольной сеток составит:

. (8.6)

Следует отметить, что создать излучатель, характеристика направленности которого быстро уменьшится за пределами сектора сканирования, достаточно сложно. В связи с этим число излучателей в реальных сканирующих решетках больше минимально возможного. Выходом из сложившегося положения является объединение слабонаправленных излучателей в подрешетки. Объединение осуществимо, если ширина ДН ФАР не превышает 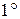, а сектор сканирования в обеих плоскостях меньше .

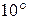Излучатели каждой подрешетки возбуждаются синфазно и формируют ДН, максимум которой ориентирован в направлении нормали к плоскости решетки. При сканировании фазы колебаний каждой подрешетки, которые можно рассматривать как отдельные излучатели антенны, изменяются с помощью фазовращателей.

Относительные размеры подрешеток выбирают в соответствии с заданным сектором сканирования и допустимым уровнем 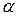дифракционных максимумов высших порядков, находящихся в пределах основного лепестка ДН подрешеток, поскольку форма ДН подрешетки отличается от прямоугольной:

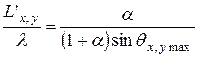. (8.7)

Число строк и столбцов, образованных подрешетками определяется выражением:

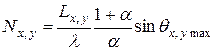. (8.8)

Число фазовращателей в решетке:

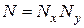. (8.9)

Размеры антенны определяются заданными значениями КНД или шириной ДН, длиной волны и выбранным амплитудным распределением поля в раскрыве антенны (последнее зависит от требуемого уровня боковых лепестков).

Так, при равномерном распределении амплитуды в прямоугольном раскрыве ширина ДН по половинной мощности неотклоненного луча определяется соотношением

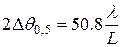град, (8.10)

уровень первых боковых лепестков составляет -13,2 дБ, а уровень остальных уменьшается пропорционально 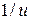, где .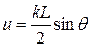

Для расчета ширины ДН линейной решетки при отклонении луча от нормали вводят понятие эквивалентной длины решетки:

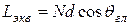. (8.10)

При увеличении угла отклонения эквивалентная длина уменьшается, а ширина ДН в соответствии с формулами увеличивается.

Для прямоугольного раскрыва вводится понятие эквивалентной площади решетки:

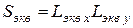. (8.11)

У плоской решетки КНД зависит от отклонения максимума ДН от нормали к плоскости решетки на угол :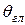

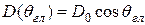. (8.12)

В данной формуле 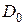‑ значение КНД в направлении перпендикуляра в плоскости решетки.