Линейные излучающие системы. Идеальный излучатель.

Под линейными антеннами следует понимать антенны, образуемые элементарными источниками, расположенными непрерывно или дискретно вдоль линии, если поперечные размеры источников много меньше продольных и длины волны.

Парциальные диаграммы направленности элементов системы предполагаются одинаковыми, что эквивалентно постулированию одинакового распределения излучающих токов внутри каждого элемента. В целом линейная излучающая система полностью определяется законом размещения центров излучателей вдоль оси и законом распределения комплексных амплитуд возбуждения по отдельным элементам, так называемым амплитудно-фазовым распределением возбуждения.

В настоящее время нет единой общепринятой классификации линейных антенн. Классификация, приведенная на рисунке 6.1, является весьма условной.

В курсе дисциплин «Электродинамика и распространение радиоволн», а также в теме «Основы теории антенн» были исследованы характеристики 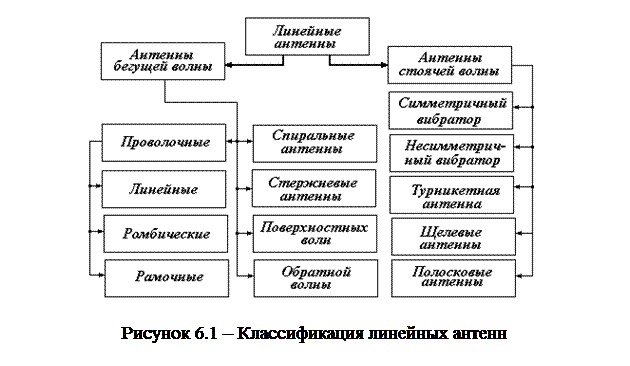отдельных антенных излучателей – вибраторов, элементов Гюйгенса, микрополосковых излучателей. Кроме того, при изучении теории, описывающей вычисление поля прямоугольного отверстия, был изложен подход к нахождению поля системы непрерывных излучателей, каждый из которых представляет собой элемент Гюйгенса. Используем данный подход и к нахождению поля линейных антенн. При этом будем рассматривать как дискретную антенную решетку размерности N, так и систему непрерывных излучателей (в случае моделирования линейного излучателя конечных размеров). Геометрия представления линейного излучателя при нахождении поля в дальней зоне проиллюстрирована на рисунке 6.2.

В соответствии с теоремой перемножения диаграмму направленности линейной излучающей системы 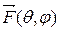представим в виде:

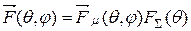, (6.1)

где 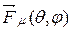‑ векторная диаграмма направленности элемента (парциальная диаграмма направленности).

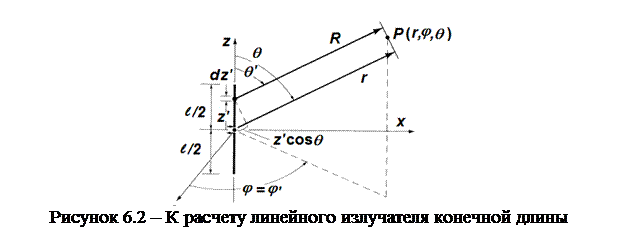Множитель направленности линейной излучающей системы 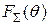в зависимости от представления системы в виде дискретных или непрерывных излучателей записывается в виде:

‑ для дискретной системы излучателей

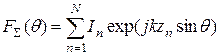; (6.2а)

‑ для непрерывной системы излучателей

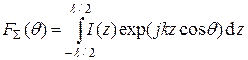, (6.2б)

где 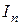‑ комплексная амплитуда возбуждения излучателя с номером n; 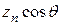‑ разность хода лучей, идущих из начала общей системы координат и из точки расположения излучателя с номером n в точку наблюдения; 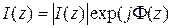‑ амплитудно-фазовое распределение по длине излучателя; 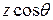‑ разность хода лучей.

Множители направленности линейных систем излучателей не зависят от азимутальной координаты и обладают симметрией вращения вокруг оси 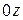. В физическом отношении данные множители описывают интерференцию сферических волн, возбуждаемых изотропными источниками. Данному сомножителю обычно уделяется основное внимание при анализе остронаправленных антенн, поскольку именно он оказывает существенное влияние на ширину главного лепестка.

Своеобразным эталоном, относительно которого оценивают свойства и параметры линейных излучателей с другими различными распределениями возбуждения является идеальный линейный излучатель, представляющий собой линейную излучающую систему с распределением возбуждения вида

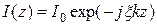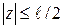при , (6.3)

где 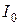‑ постоянная амплитуда; 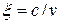‑ коэффициент замедления фазовой скорости возбуждения v по отношению к скорости света c.

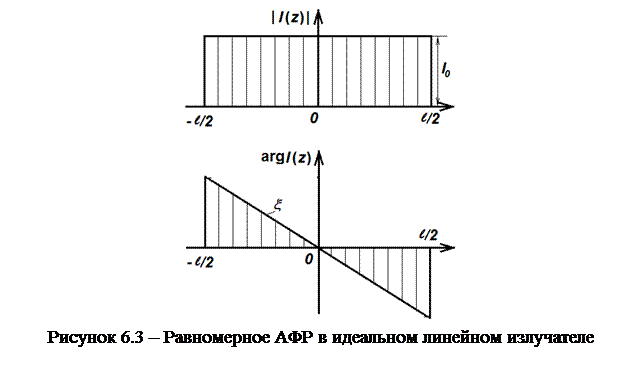Распределение амплитуды возбуждения в идеальном излучателе равномерно, а распределение фазы подчиняется линейному закону, характерному для бегущей вдоль координаты z волны (рисунок 6.3).

Подстановка распределение тока (6.3) в соотношение (6.2б) позволяет записать замкнутое выражение для множителя направленности идеального линейного излучателя:

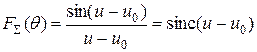, (6.4)

где 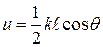, , 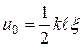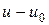‑ новая обобщенная угловая переменная, имеющая смысл половины разности фаз колебаний, приходящих в удаленную точку наблюдения из крайних точек излучателя, с учетом как пространственной разности хода 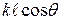, так и полной разности фаз возбуждения крайних точек излучателя.

Фазовый центр линейного идеального излучателя находится в его середине.