Оценка адекватности и точности модели тенденции
После построения модели тенденции осуществляется проверка ее качества по характеристикам адекватности (соответствия данным наблюдения) и точности.
Проверка адекватностимодели основывается на анализе ряда остатков
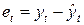, (i = 1, 2, ..., n) (16.21)
Модель считается адекватной, если остатки:
– являются случайными;
– распределены по нормальному закону;
– имеют равное нулю среднее значение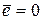 
;
– независимы между собой.
1) Проверка случайности остатков заключается в установлении факта отсутствия или наличия тенденции остатков. Для этой цели может использоваться критерий серий. Предварительно определяется медиана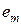 
упорядоченного ряда остатков. Каждому элементу ряда остатков 
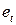ставится в соответствие знак «+», если 
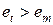,и знак «–», если 
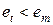.Непрерывно идущую последовательность одинаковых знаков принято называть серией. Определяется максимальная длина серии 
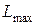и число серий V. Остатки считаются случайными на уровне значимости 0,05, если одновременно выполняются два условия
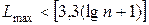, (16.22)
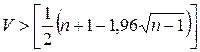. (16.23)
2) Нормальность распределения остатков считается установленной (приближенно) если одновременно выполняются следующие неравенства:
; 
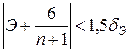, (16.24)
где А – выборочная характеристика асимметрии, Э – выборочная характеристика эксцесса,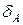 
, 
– среднеквадратические ошибки выборочных характеристик асимметрии и эксцесса, определяемые соотношениями
; 
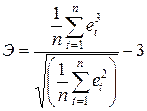; (16.25)
; 
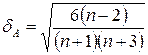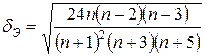; (16.26)
Если же выполняется хотя бы одно из неравенств
; 
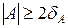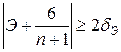, (16.27)
то гипотеза о нормальном характере распределения остатков отвергается. Другие случаи требуют дополнительной проверки с помощью более мощных критериев.
3) Проверка равенства нулю среднего значения ряда остатков 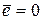осуществляется с помощью критерия Стьюдента. Гипотеза о равенстве нулю 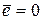отвергается, если выполняется условие
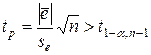, (16.28)
где
.
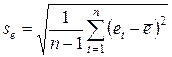4) Под независимостью ряда остатков понимается отсутствие в нем автокорреляции, т. е. отсутствует зависимость каждого значения ряда от предыдущих значений. Если вид функции, описывающей систематическую составляющую, выбран неудачно, то последовательные значения ряда остатков могут коррелировать между собой.
Для проверки ряда остатков на отсутствие автокорреляции уровней остатков используется критерий Дарбина-Уотсона. Этот критерий основан на расчете величины
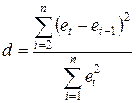, (16.29)
представляющей собой отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.
Между критерием Дарбина-Уотсона d и коэффициентом автокорреляции остатков первого порядка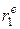 
имеет место следующее соотношение:
. (16.30)
Таким образом, если в остатках существует полная положительная автокорреляция и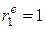 
, то d = 0. Если в остатках полная отрицательная автокорреляция, то 
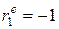и, следовательно, d = 4. Если автокорреляция остатков отсутствует, то 
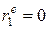и d = 2. Величина d изменяется в диапазоне 
.
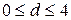Применение критерия Дарбина-Уотсона для выявления автокорреляции остатков осуществляется в следующей последовательности.
а) Выдвигается нулевая гипотеза Н0об отсутствии автокорреляции остатков. Альтернативные гипотезы Н1 и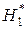 
состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках.
б) По таблицам критерия Дарбина-Уотсона (см. приложение) определяются критические значения критерия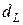 
и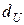 
для заданного числа наблюдений п,числа факторов модели 
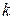и уровня значимости 
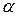. Этими значениям числовой промежуток [0; 4] разбивается на пять отрезков (0, ),( , 
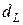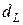), ( ,4- ),(4- 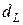,4- ),(4- 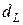,4) (рис. 16.3).
в) Выдвинутые гипотезы принимаются или отклоняются с вероятностью (1- 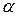) в зависимости от того, в какой отрезок попадет значение критерия d:
(0, 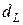)– принимается Н1,остатки имеют положительную корреляцию;
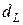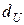( , )– зона неопределенности;
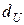( , 4- 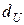) – принимается 
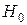,автокорреляция остатков отсутствует;
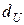(4- , 4- 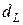) – зона неопределенности;
(4- 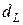,4) – принимается 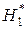,остатки имеют отрицательную корреляцию. Применение критерия иллюстрирует рис. 16.2.
| Есть положительная автокорреляция остатков. Н0 отклоняется. С вероятностью Р = (1 – a) принимается H1 | Зона неопределенности | Нет оснований отклонять Н0 (автокорреляция остатков отсутствует) | Зона неопределенности | Есть
отрицательная
автокорреляция
остатков.
Н0 отклоняется.
С вероятностью
Р = (1 – a)
принимается
|
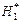
0 dL dU 24-dU 4-dL 4
Рис. 16.3. Алгоритм проверки гипотезы о наличии автокорреляции остатков
К недостаткам критерия Дарбина-Уотсона относится наличие области неопределенности и то, что осуществляется проверка зависимости между ближайшими уровнями ряда.
Другим методом проверки наличия автокорреляции остатков является тест серий (Бреуша-Годфри),основанный на оценке значимости коэффициентов авторегрессионного уравнения
,(16.31)
полученных методом наименьших квадратов. Наличие значимых коэффициентов говорит об имеющейся автокорреляции остатков и ее характере.
Оценка точностимодели тенденции заключается в оценке близости модельных значений тенденции к фактическим уровням ряда и осуществляется с помощью вычисления таких показателей, как:
– дисперсия остатков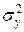 
;
– средняя ошибка аппроксимации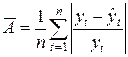 
;
– коэффициент детерминации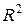 
.
Дата добавления: 2015-11-06; просмотров: 2060;