В точке сплошной среды.
В совремённой геомеханике широко используются понятия механики сплошной среды, в основу которой положены представления о материальных телах как «о некоторой субстанции, непрерывно заполняющей объем геометрического пространства и наделенной определенными физическими свойствами, отражающими статистические закономерности для реальных физических сред».
Введенное предположение о сплошности среды позволяет наделять бесконечно малые объемы тел свойствами среды и эффективно использовать аналитический аппарат дифференциального и интегрального исчисления. В частности, напряжения и перемещения отдельных точек среды представлять в виде некоторых функций координат и времени, непрерывных и дифференцируемых вплоть до такого порядка производных, который обеспечивал бы требуемую точность решения задачи.
В механике сплошных сред различают две категории сил: внешние и внутренние.
Внешние силы—это приложенные к рассматриваемому объекту силы, вызываемые действием других тел. Их подразделяют на поверхностные и объемные.
Поверхностные силы (например, давление) приложены к поверхности тела и характеризуют конкретное взаимодействие его с другими телами.
Объемные или массовые силы приложены к внутренним частям тела (силы веса, силы инерции и др.).
Внутренние силы — это силы связи между отдельными физическими частицами вещества. Внутренние силы под влиянием внешних изменяются, получают приращения, которые и являются основным предметом изучения механики деформируемых тел.
Кроме того, под воздействием внешних сил изменяются также положения отдельных точек в теле, расстояния между ними, т. е. тело деформируется.
Таким образом, определить напряженно-деформируемое состояние какого-либо тела под влиянием приложенных внешних сил — это значит определить в каждой его точке значения приращений внутренних сил и перемещений его точек в пространстве.
Как внешние, так и внутренние силы обычно характеризуют их интенсивностью, т. е. усилием, приходящимся на единицу площади поверхности или объема тела.
При рассмотрении внутренних сил эту интенсивность называют напряжением. В общем случае напряжения являются функциями:
n координат;
n ориентировки бесконечного малого элемента площади ds в пространстве деформируемого тела;
n времени.
Напряжение р как вектор может быть представлено в виде трех взаимоперпендикулярных составляющих. Две из них располагаются в плоскости сечения и называются касательными напряжениями t. Составляющую, направленную перпендикулярно к плоскости сечения, называют нормальной составляющей или нормальным напряжением s.Таким образом, напряженное состояние по любой элементарной площадке может быть однозначно охарактеризовано тремя составляющими напряжений.
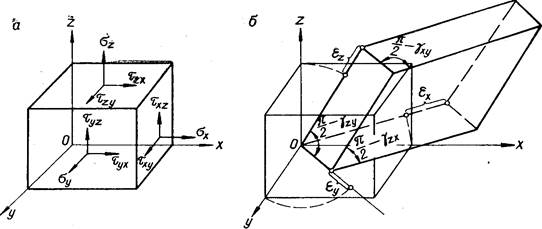
Вместе с тем три взаимоперпендикулярные площадки характеризуют элементарный объем. В соответствии с этим напряженное состояние элементарного объема может быть определено девятью компонентами напряжений - тремя нормальными и шестью касательными составляющими напряжений (рис.1.1, а).
Однако, ещё в курсе сопротивления материалов рассматривался закон парности касательных напряжений, который выводится из условия равновесия выделенного элементарного объема. Напомним, что условие равновесия может быть соблюдено, если главный или результирующий вектор и главный момент всех внешних сил, действующих на рассматриваемый материальный объем, равны нулю.
Если составить уравнения моментов всех сил относительно каждой из осей Ох, Оу и Оz (см. рис. 1.1) и приравнять их нулю, то легко может быть выведено, что
txy = tyx; tyz = tzy; tzx = txz(1.1)
|
Таким образом, всего неизвестных компонентов напряжений будет шесть.
Рис. 1.1. Напряженно-деформированное состояние элементарного объема в декартовых координатах.
а—напряжения на гранях элементарного объема; б—деформации элементарного объема.
Расположим все напряжения, определяющие собой напряжённое состояние в рассматриваемой точке, в виде следующей таблицы (матрицы):
| sx | txy | txz |
| tyx | sy | tyz |
| tzx | tzy | sz |
Здесь в первой строке расположены все компоненты, имеющие направление, параллельное оси Х, соответственно во второй строке - все компоненты, имеющие направление, параллельное оси У, в третьей - все компоненты, имеющие направление, параллельное оси Z.
Кроме того, в первом столбце сгруппировались напряжения, действующие на площадке, нормаль к которой параллельна оси Х, во втором столбце - все напряжения на площадке с нормалью, параллельной оси У, в третьем столбце - на площадке с нормалью, параллельной оси Z.
При таком способе построения нормальные напряжения расположились по главной диагонали, а одинаковые по величине касательные напряжения - симметрично относительно её.
Эту симметричную табличку (матрицу) называют тензором напряжений.Таким образом, можно констатировать, чтонапряжённое состояние в заданной точке в данный момент вполне определено, если задан тензор напряжений для этой точки и для того же момента времени.
У данной матрицы имеются некоторые замечательные свойства, рассмотрение которых расширяет наши представления о напряжённом состоянии в точке. В частности, через каждую пространственно напряжённую точку можно провести несколько замечательных плоскостей, на которых действующие напряжения являются характерными.
Так существуют три взаимно перпендикулярные площадки, по которым касательные напряжения равны нулю, а действующие на них нормальные напряжения имеют характерные для данной точки значения - максимум, минимум и минимакс. Это есть главные площадки для нормальных напряжений. Значения напряжений на этих площадках называются главными нормальными напряжениями.
Также можно выделить три пары площадок, которые делят пополам двугранные углы между главными площадками нормальных напряжений. Значения касательных напряжений на этих площадках являются максимальными и равны полуразности соответствующих нормальных напряжений. Нормальные напряжения на этих площадках равны соответственно полусуммам главных нормальных напряжений.
Эти площадки называются главными площадками для касательных напряжений.
Кроме понятия напряжение в данной точке тела в теории сплошных сред применяют также понятие деформацияв данной точке тела, которое характеризует относительное изменение расстояний между точками тела в результате приложенных внешних сил. Подобно напряжениям деформации являются функциями:
* координат;
* ориентировки бесконечно малого элемента длины dl в пространстве деформируемого тела;
* времени.
Полная деформация еаналогично напряжению может быть также представлена в виде трех взаимно перпендикулярных составляющих. Одна из них обусловливает линейные деформации тела e (удлинения или укорочения), а две другие перпендикулярны к ней и соответствуют сдвиговым деформациям g (рис.1.1, б).
Деформирование любого объема может быть охарактеризовано деформациями трех взаимно перпендикулярных отрезков. Поэтому, как и для напряжений, деформированное состояние какого-либо объема может быть однозначно определено девятью компонентами.
Девять компонент деформаций также составляют тензор деформаций в данной точке:
| ex | 0.5gxy | 0.5gxz |
| 0.5gyx | ey | 0.5gyz |
| 0.5gzx | 0.5gzy | ez |
Здесь необходимо обратить лишь внимание на коэффициент 0.5, который присутствует при сдвиговых деформациях.
Вообще существует полная аналогия между теорией напряжений в точке и теорией деформаций. Поэтому всё, что было сказано относительно напряжений полностью справедливо и для деформаций.
Так аналогично напряжениям через каждую точку деформируемого тела можно провести три взаимоперпендикулярные направления, сдвиги между которыми равны нулю и по которым действуют только линейные деформации «удлинения - укорочения» - главные оси деформации.
Другими словами, эти направления были взаимоперпендикулярными до деформации и остались взаимоперпендикулярными после деформации.
Через ту же точку можно провести направления, по которым угловые деформации оказываются максимальными по величине и равны полуразностям главных линейных деформаций, а линейные деформации по этим направлениям равны полусумме соответствующих главных линейных деформаций.
Дата добавления: 2015-11-06; просмотров: 980;
