КОЛЕБАНИЯ. СПЕКТРЫ. РЕЗОНАНС

Колебаниями называются повторяющиеся процессы изменения каких-либо параметров системы (например, перепады температур, биение сердца, движение Луны и т. д.).

Механические колебания — это повторяющиеся движения различных тел (вращение Земли и планет, колебания маятников, камертонов, струн и др.).

Периодические колебания лежат в основе создания музыкальных звуков, так как только по периодическим колебаниям слуховая система идентифицирует высоту тона.

Простое гармоническое колебание можно определить как колебание тела, смещение которого описывается по формуле:

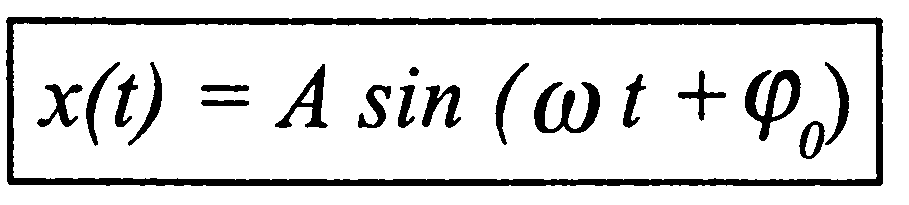
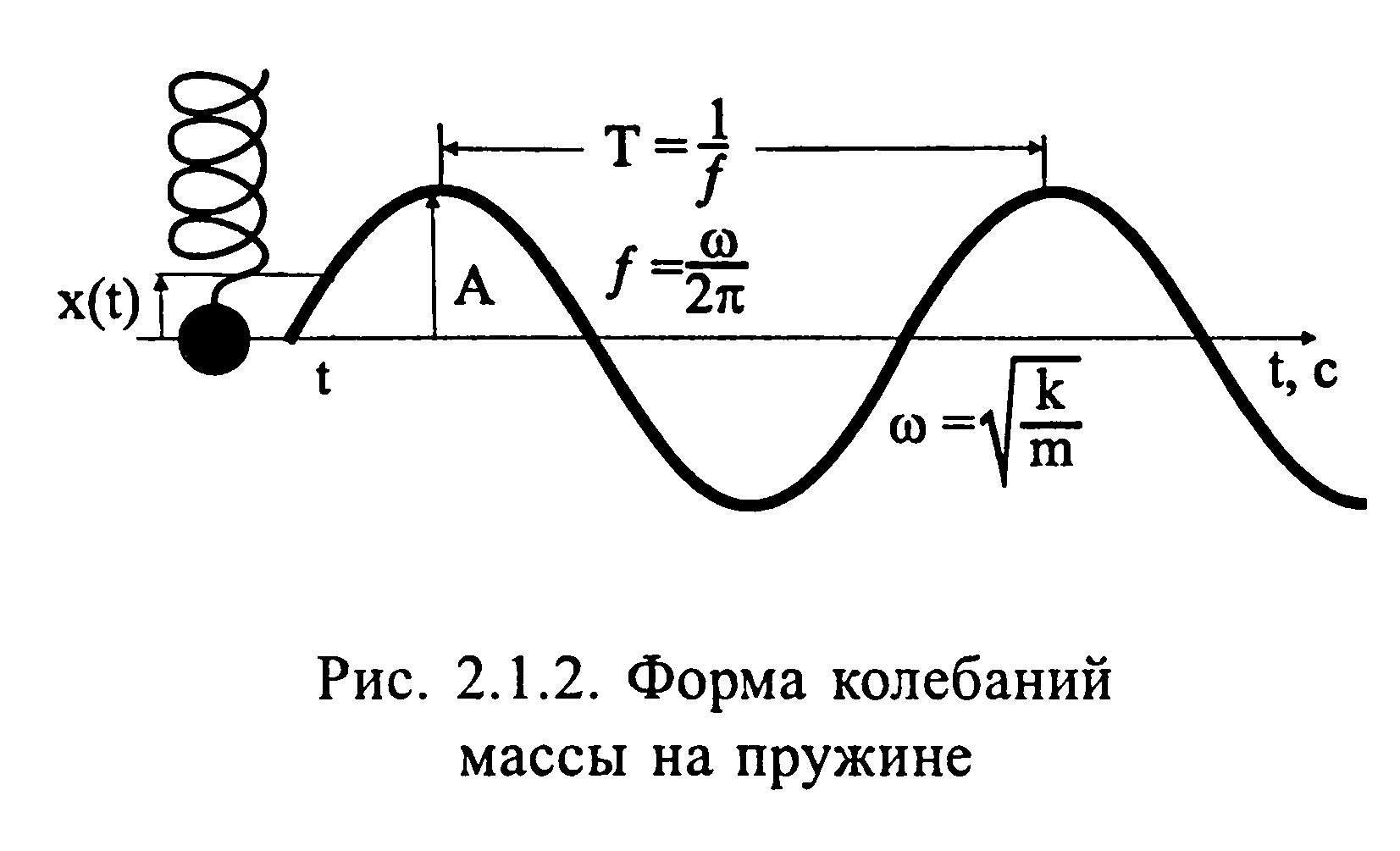
А — амплитуда колебаний. Амплитудой колебаний называется максимальное смещение тела от положения равновесия (при установившихся колебаниях она постоянна) (рис. 2.1.2).

T — период колебаний. Периодом колебаний называется наименьший промежуток времени, через который колебания повторяются (рис. 2.1.2). Измеряется в сек. Например, если маятник проходит полный

цикл колебаний (в одну и другую сторону) за 0,01 с, то его период колебаний равен этой величине: T = 0,01 с. Для простого гармонического колебания период не зависит от амплитуды колебаний.

f — частота колебаний. Частота колебаний определяется числом колебаний (циклов) в секунду. Единица ее измерения равна одному колебанию в секунду и называется герц (Гц).

Частота колебаний — это величина, обратная периоду: f = 1/Т.

Например, если период колебаний равен T = 0,01 с, то частота колебаний равна:

f= 1/Т = 1/0,01 с = 100 Гц.

со — угловая (круговая) частота. Угловая частота связана с

частотой колебаний по формуле со = 2т$, где число к = 3,14. Она

измеряется в радианах в секунду (рад/с). Например, если частота

f = 100 Гц, то со = 628 рад/с.

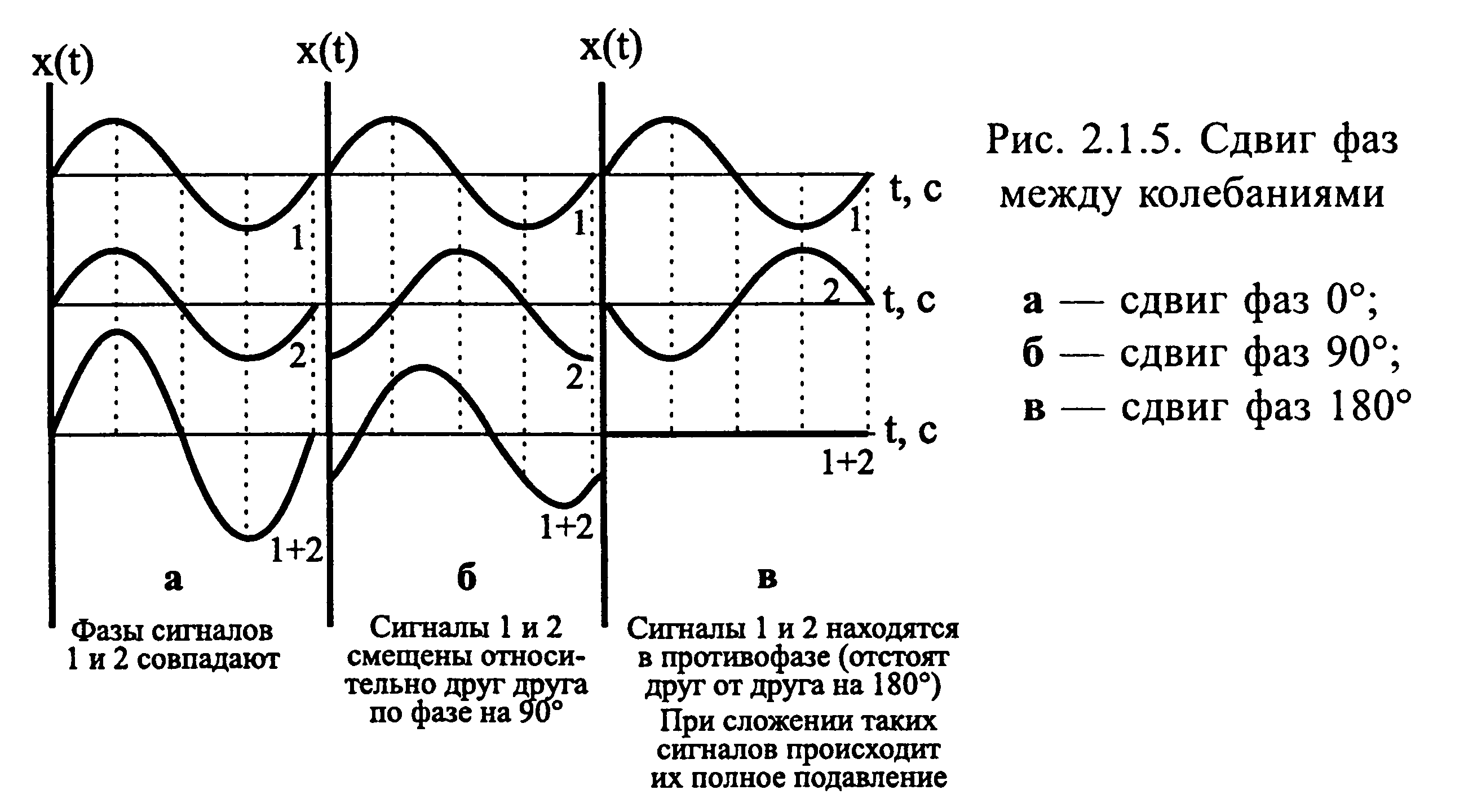
ω— начальная фаза. Начальная фаза определяет положение тела, с которого началось колебание. Она измеряется в градусах. Например, если маятник начал колебаться из положения равновесия, то его начальная фаза равна нулю. Если маятник сначала отклонить

в крайнее правое положение и затем толкнуть, он начнет колебания с начальной фазой 90°. Если два маятника (или две струны, мембраны и др.) начнут свои колебания с задержкой во времени, то между ними образуется сдвиг фаз (рис. 2.1.5); если задержка во времени равна одной четверти периода, то сдвиг фаз — 90°, если половине периода —180°, трем четвертям периода — 270°, одному периоду — 360°. Если какое-то тело (пружину, маятник, струну, камертон и др.) вывести из положения равновесия (т. е. приложить силу и отпустить), то оно будет совершать свободные периодические колебания с определенной частотой, которая зависит только от его жесткости и массы.

Такая частота называется собственной частотой колебаний. Частота собственных колебаний тела (например, массы на пружине или струны) может быть представлена как:

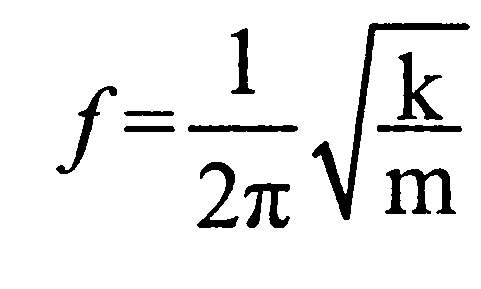
где к — жесткость тела, m — его масса.

Частота собственных колебаний струны:

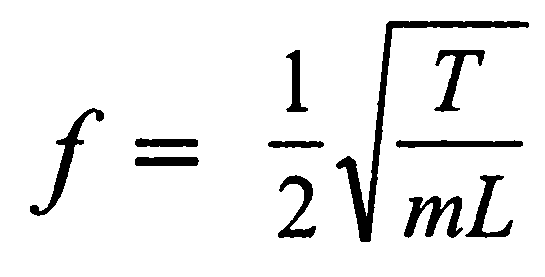
Струна длиной L, массой m и натяжением T имеет основную собственную частоту.

Эту же формулу можно записать в несколько другом виде, если представить массу как произведение поверхностной плотности материала струны на ее длину: m = pL , то

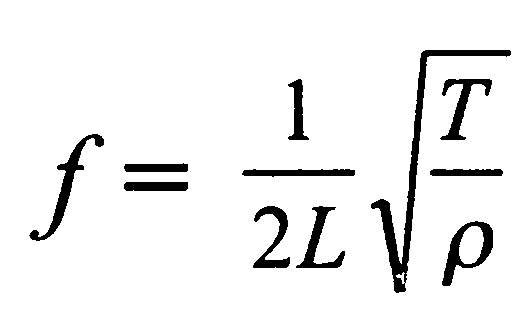
Моды – формы колебаний на разных собственных частотах.

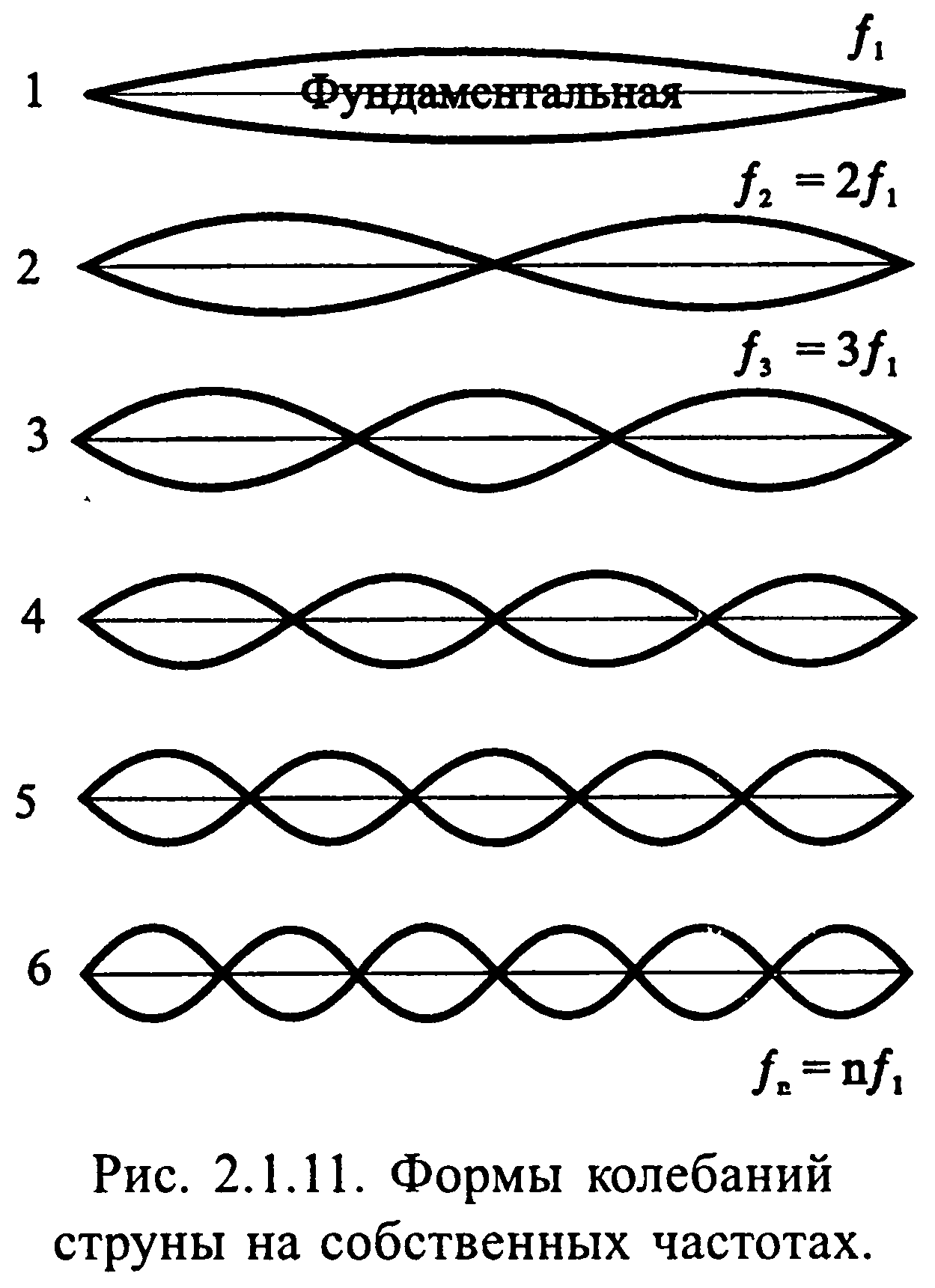
Набор собственных частот и амплитуд колебаний, которые воз-

буждаются в данном теле при воздействии на него внешней силы

(ударом, щипком, смычком и др.), называется амплитудным спектром

При возбуждении реальных тел они совершают колебания сложной формы, которые могут быть представлены в виде суммы одновременных колебаний с различными собственными частотами и амплитудами (метод представления называется анализом Фурье).

Первая основная (низшая) собственная частота называется фундаментальной частотой

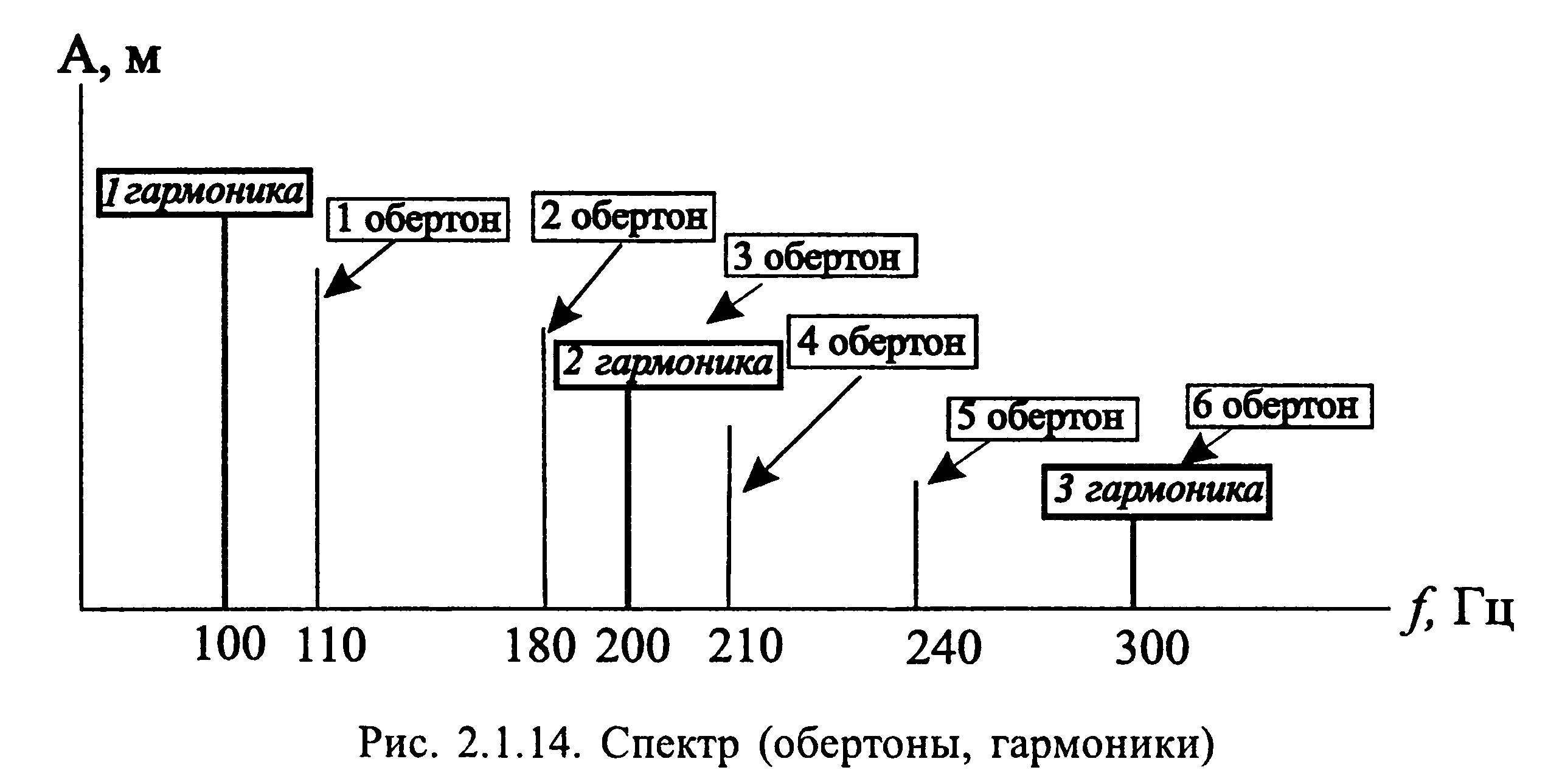
(иногда ее называют основной частотой). Все собственные частоты выше первой называются обертонами, например на рис. 2.1.14.

фундаментальная частота 100 Гц, первый обертон — 110 Гц, второй обертон — 180 Гц и т. д. Обертоны, частоты которых находятся в целочисленных соотношениях с фундаментальной частотой, называются гармониками (при этом фундаментальная частота называется первой гармоникой). Например, на рис. 2.1.14 третий обертон является второй гармоникой, поскольку его частота равна 200 Гц, т. е. относится к фундаментальной частоте как 2:1.

Слуховая система легко определяет частоту, если обертоны и гармоники совпадают. Если нет, то значит, звучит перкуссия (барабан, тарелка).