Организация двусвязанного списка.

Пример через класс (хранимое данное: нетипизированный указатель (void*)). Особенностью списка является отсутствие управляющей структуры данных, операции над списком могут быть выполнены над любым элементом. Другой особенностью является «закольцованность», т.е. после последнего элемента идёт опять первый, перед первым – последний. Это позволяет в любой момент выбрать любой элемент списка в качестве первого.

class List

{

private:

List *next,*prev; //адрес следующего и предыдущего элементов

int *cnt; //указатель на количество элементов списка

public:

bool linkdata; //удалять ли связанные данные при удалении элемента

void *data; //указатель на данные

protected:

//закрытый «быстрый» конструктор, используется для добавления элемента

List(void* data,int *cnt):data(data),linkdata(false),cnt(cnt)

{

}

public:

//открытый конструктор создающий новый несвязанный элемент, на основе которого может быть построен //новый список

List(void* data = NULL):data(data),linkdata(false)

{

prev=next=this;

cnt = new int(1); //создаётся новый счётчик числа элементов

}

virtual ~List() //деструктор

{

if (linkdata&&data!=NULL) free(data);//если есть данные и они «связаны», то удаляем их

next->prev=prev; prev->next=next; //переопределение связей

--(*cnt); //уменьшение количества элементов списка

if (*cnt==0) delete cnt; //если это последний элемент, то удаляем и счётчик

}

inline List* Next() {return next;} //следующий элемент

inline List* Prev() {return prev;} //предыдущий элемент

inline List* PushAfter(void* data = NULL) //добавить элемент после текущего

{

List *t = new List(data,cnt); //создаём новый элемент

if (t==NULL) return NULL; //если создание неуспешно, возврат

t->prev = this; //переопределение связей

t->next = next;

t->data = data;

next->prev = t;

next = t;

++(*cnt); //увеличение счётчика

return t;

}

void Clear() //очистка списка, остаётся только текущий элемент

{

List *t = next;

while (t!=this)

{

if (t->linkdata) free(t->data);

t = t->next;

delete t->prev;

}

cnt = 1;

next = prev = this;

}

inline int Count() {return *cnt;} //количество элементов

};

Организация на языке «С» (struct)

struct List

{

List *next,*prev;

int *cnt;

void *data;

char linkdata;

}

int Init(List* element)

{

element->prev= element->next= element;

if (element->cnt = malloc(sizeof(int))==NULL) return -1;

return 0;

}

List* PushAfter(List* elenemt, void* data)

{

List *t = malloc(sizeof(List));

if (t==NULL) return NULL;

t->data = data;

t->cnt = cnt;

t->linkdata = 0;

t->prev = element;

t->next = element->next;

t->data = element->data;

element->next->prev = t;

element->next = t;

++(*element->cnt);

return t;

}

int Delete(List* element)

{

if (element->linkdata&&element->data!=NULL) free(data);

element->next->prev= element->prev; element->prev->next=element->next;

--(*element->cnt);

if (*element->cnt==0) free(element->cnt);

free(element);

}

Организация массива переменного размера:

1. С быстрым извлечением – создаётся вектор размера top, если происходит попытка записи элемента с номером n больше top, происходит перевыделение памяти так, чтобы (n < top). Может дополнительно задаваться шаг роста массива. Далее существующие данные копируются в новый массив; освобождается место, где ранее размещался массив. Недостаток – существенные временные затраты на «рост».

2. С быстрым расширением – создаётся список векторов, инициализируется только первый вектор (размер top). При попытке записи элемента с номером n больше top к списку добавляются один или несколько векторов, чтобы (n<top). Для ускорения доступа все векторы целесообразно создавать одного размера. Доступ к элементу осуществляется по номеру вектора (k) и номеру элемента в векторе (m). При равных размерах векторов (top) и заданном порядковом номере элемента (n) получаем: k=n/top, m=n%top.

В качестве модификации можно использовать вектор векторов (несколько быстрее доступ, но сложнее организовать рост).

class Vector

{

protected:

void** data; //поле данных

int top,step; //верхняя граница и шаг роста

public:

//конструктор принимает аргументы: начальный размер вектора и шаг роста

tVector(int top = 10, int step = 10):top(top),step(step)

{

data = (void**)malloc(top*sizeof(void*));

memset(data,0,top*sizeof(void*)); //сброс всех данных в ноль

}

~tVector()

{

free(data);

}

void* GetAt(int n)

{

if (n>-1 && n<top) return data[n];

return NULL; //если данные за допустимым диапазоном

}

bool SetAt(int n, void* element)

{

if (n>=top) //рост массива если вышли за границы

{

int oldtop = top;

while((top+=step)<=n);

void **tdata = (void**)malloc(top*sizeof(void*));

if (tdata == NULL) return false;

memcpy(tdata,data,oldtop*sizeof(void*));

memset(tdata+oldtop,0,(top-oldtop)*sizeof(void*));

free(data);

data = tdata;

}

*(data+n) = element;

return true;

}

int Count() {return top;} //верхняя граница

};

Библиотека STL (standard template library) предоставляет стандартные классы структур данных.

deque – очереди;

list – двусвязанный список;

vector – вектор;

map / multimap – карта – каждый элемент задаётся двумя аргументами: ключом и значением;

set / multiset – множество.

multi- соответствует возможности множественного вхождения.

Организация бинарного дерева.

class Tree

{

class Node

{

public void *item;

public Node *left,*right;

public Node(void* item) { this->item = item;}

}

}

Алгоритмы

Быстрая сортировка

"Быстрая сортировка", хоть и была разработана более 40 лет назад, является наиболее широко применяемым и одним их самых эффективных алгоритмов.

Метод основан на подходе "разделяй-и-властвуй". Общая схема такова:

из массива выбирается некоторый опорный элемент a[i],

запускается процедура разделения массива, которая перемещает все ключи, меньшие, либо равные a[i], влево от него, а все ключи, большие, либо равные a[i] - вправо,

теперь массив состоит из двух подмножеств, причем левое меньше, либо равно правого,

для обоих подмассивов: если в подмассиве более двух элементов, рекурсивно запускаем для него ту же процедуру.

В конце получится полностью отсортированная последовательность.

Рассмотрим алгоритм подробнее.

Разделение массива

На входе массив a[0]...a[N] и опорный элемент p, по которому будет производиться разделение.

Введем два указателя: i и j. В начале алгоритма они указывают, соответственно, на левый и правый конец последовательности.

Будем двигать указатель i с шагом в 1 элемент по направлению к концу массива, пока не будет найден элемент a[i] >= p. Затем аналогичным образом начнем двигать указатель j от конца массива к началу, пока не будет найден a[j] <= p.

Далее, если i <= j, меняем a[i] и a[j] местами и продолжаем двигать i,j по тем же правилам...

Повторяем шаг 3, пока i <= j.

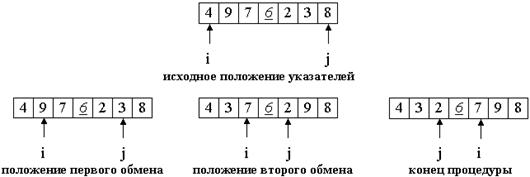
Рассмотрим работу процедуры для массива a[0]...a[6] и опорного элемента p = a[3].

Теперь массив разделен на две части: все элементы левой меньше либо равны p, все элементы правой - больше, либо равны p. Разделение завершено.

Реализация на Си.

template<class T>

void quickSortR(T* a, long N) {

// На входе - массив a[], a[N] - его последний элемент.

long i = 0, j = N; // поставить указатели на исходные места

T temp, p;

p = a[ N/2]; // центральный элемент

// процедура разделения

do {

while ( a[i] < p ) i++;

while ( a[j] > p ) j--;

if (i <= j) {

temp = a[i]; a[i] = a[j]; a[j] = temp;

i++; j--;

}

} while ( i<=j );

// рекурсивные вызовы, если есть, что сортировать

if ( j > 0 ) quickSortR(a, j);

if ( N > i ) quickSortR(a+i, N-i);

}

Каждое разделение требует, очевидно, Theta(n) операций. Количество шагов деления(глубина рекурсии) составляет приблизительно log n, если массив делится на более-менее равные части. Таким образом, общее быстродействие: O(n log n), что и имеет место на практике.

Однако, возможен случай таких входных данных, на которых алгоритм будет работать за O(n2) операций. Такое происходит, если каждый раз в качестве центрального элемента выбирается максимум или минимум входной последовательности. Если данные взяты случайно, вероятность этого равна 2/n. И эта вероятность должна реализовываться на каждом шаге... Вообще говоря, малореальная ситуация.

Метод неустойчив. Поведение довольно естественно, если учесть, что при частичной упорядоченности повышаются шансы разделения массива на более равные части.

Сортировка использует дополнительную память, так как приблизительная глубина рекурсии составляет O(log n), а данные о рекурсивных подвызовах каждый раз добавляются в стек.

Поиск пути

На гребне волны...

Один из самых простых для понимания алгоритмов поиска путей и вместе с тем довольно эффективный — волновой поиск. Он идеально подходит для небольших карт, которые можно представить в виде двумерного массива ячеек. Для начала вам нужно завести еще один двумерный массив целых чисел такого же размера.

Алгоритм работает следующим образом. Находим точку А, из которой начинается поиск, и в этом месте в вспомогательном массиве ставим 0. Во всех свободных ячейках, которые прилегают к ячейке с нулем, пишем 1. Во всех свободных от цифр и препятствий ячейках, которые прилегают к ячейкам с 1, пишем 2. Повторяем этот процесс для всех остальных ячеек, пока не дойдем до ячейки B, путь до которой нам требовалось найти. Если вы визуализируете этот процесс в динамике, то увидите, что от точки A разбегается волна из цифр. Отсюда и название алгоритма. Как только наша цифровая волна захлестнет точку B, строим от нее путь до точки A по правилу: следующая точка пути должна лежать в ячейке с меньшим, чем в текущей ячейке числом.

Алгоритм неплохо справляется с разного рода тупиками и всегда найдет путь из A в B, если он вообще существует. Другое дело, что этот путь редко будет кратчайшим из возможных. К сожалению, волновой поиск нельзя использовать на больших картах (с десятком тысяч и более клеток), так как он работает очень медленно.

Поиск в глубину

Предыдущий алгоритм иногда называют поиском в ширину, потому что он уровень за уровнем просматривает ближайшие клетки. Поиск в глубину выбирает какое-то одно направление и просматривает его вглубь на заданное число клеток, переходит к следующему направлению и так далее, пока не найдет конечную точку. Представленная ниже рекурсивная функция находит не все возможные пути. Чтобы найти кратчайший путь, надо вызвать эту функцию для каждой из клеток, прилегающих к начальной клетке. Во вспомогательном булевом массиве Mark такого же размера, как и остальная карта, хранится 1, если текущая клетка уже пройдена алгоритмом, и 0 — в противном случае. В переменных Destination_x и Destination_y должны храниться координаты точки, куда в итоге надо попасть. В глобальной перемененной Length будет храниться длина текущего пути, чтобы мы не залетели вглубь матрицы дальше, чем MAX_LENGTH.

Procedure DepthSearch(x,y:integer);

Var

i : integer;

Begin

If Length>MAX_LENGTH then exit;

Mark[x,y] := True;

If (x=Destination_x) and (y=Destination_y) then

Begin

{

Мы нашли эту точку! Искомый путь представлен значениями True в массиве Mark. Здесь вы можете запомнить построенный путь и очистить Mark[x,y], чтобы продолжить поиск, или же остановиться, если задачей было найти хотя бы один путь.

}

End;

Length:=Length+1;

If Mark[x+1,y]=false then DepthSearch(x+1,y);

If Mark[x,y+1]=false then DepthSearch(x,y+1);

If Mark[x+1,y+1]=false then DepthSearch(x+1,y+1);

If Mark[x-1,y-1]=false then DepthSearch(x-1,y-1);

If Mark[x-1,y]=false then DepthSearch(x-1,y);

If Mark[x,y-1]=false then DepthSearch(x,y-1);

Length:=Length-1;

End;

В некоторых случаях этот алгоритм работает быстрее, чем волновой, но у него есть свой недостаток: если точка, путь до которой надо найти, находится дальше, чем MAX_LENGTH, алгоритм ее не найдет. Можно снять это ограничение, но тогда появится опасность зацикливания. Поиск в глубину хорошо работает в случае больших лабиринтов с узкими проходами. На широких открытых пространствах лучше использовать поиск в ширину.

Примеры программ

Половинное деление

int Find(int *array, int size)

{

int a = 0,b = size-1,t;

do

{

t = (b+a)/2;

if (m[t] == x)return t;

if (m[t]>x) b = t;

else a = t;

}while (b-a>1);

if (m[a] == x) return a;

if (m[b] == x) return b;

return -1;

}

Сортировка пузырьком

int t;

char flag;

do

{

flag = 0;

for(int i=0;i<N-1-i;i++)

if (m[i]>m[i+1]) {t=m[i];m[i]=m[i+1];m[i+1]=t;flag=1;}

}while(flag)

Обход дерева

struct Node

{

Node *parent,*left,*right;

};

void Action(Node *node)

{

if (node == NULL) return;

//action;

Action(node->left);

Action(node->right);

}

void Action2(Node *node)

{

queue<Node*> q;

q.push(node);

do

{

node = q.front();

q.pop();

//action

if (node->left!=NULL) q.push(node->left);

if (node->right!=NULL) q.push(node->right);

}

while(!q.empty)

}

Список литературы

1. Иванова Г.С. Технология программирования: Учебник для вузов. – М.: МГТУ им. Н.Э.Баумана, 2002.

2. Подбельский В.В. Язык С++: Учебн. пособие. – М.: Финансы и статистика, 1995.

3. Г. Майерс. Надёжность программного обеспечения. 1976 // Перев. на русский язык под ред. И.А.Махован и др. – М.: Мир, 1980.

4. В. В. Шураков. Надежность программного обеспечения систем обработки данных : учеб. для вузов. Изд. 2-е, пеpеpаб. и доп. — М. : Финансы и статистика, 1987 .— 272 с

5. Электронная энциклопедия ru.wikipedia.org

[1] http://ru.wikipedia.org/wiki/C

[2] Квадратные скобки не являются частью записи формата, а указывают на необязательность аргумента