КОМПЛЕКСНА ФОРМА РЯДУ ФУР’Є
Користуючись формулами Ейлера, кожний доданок в сумі (2.5) можна записати у формі
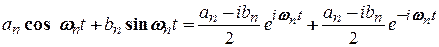 .
.
Позначаючи для 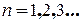
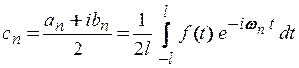 ,
, 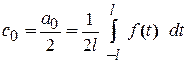 ,
,
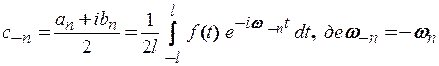 ,
,
приходимо до комплексної форми ряду Фур’є:
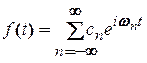 ,
,  .
.
В цьому випадку рівність Парсеваля записується так:
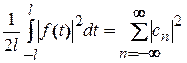 .
.
Для дійсних 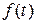 коефіцієнти
коефіцієнти 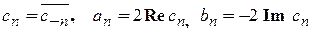 .
.
Оскільки при цьому амплітуди  і фази
і фази 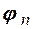 з формул (2.8), (2.9) дорівнюють
з формул (2.8), (2.9) дорівнюють
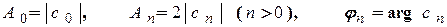 ,
,
то у випадку, коли дійсний сигнал розкладено в комплексний ряд Фур’є, то амплітудним та фазовим спектром цього сигналу називають відповідно сукупність величин

2.4 Розкладання в ряд Фур’є функцій,
які визначені на відрізку
Розкладання в ряд Фур’є функцій, які визначені на 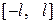
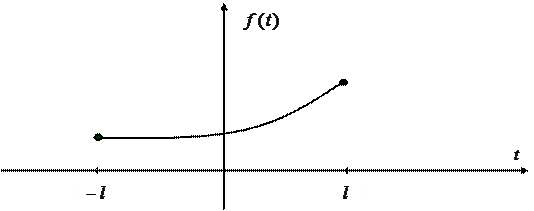 Нехай функція
Нехай функція 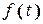 , що задана на
, що задана на 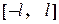 (див. рисунок 2.7), є кусково гладкою на
(див. рисунок 2.7), є кусково гладкою на 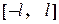 .
.
Рисунок 2.7
 Продовжимо її з
Продовжимо її з 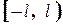 періодично на усю вісь (див. рисунок 2.8).
періодично на усю вісь (див. рисунок 2.8).
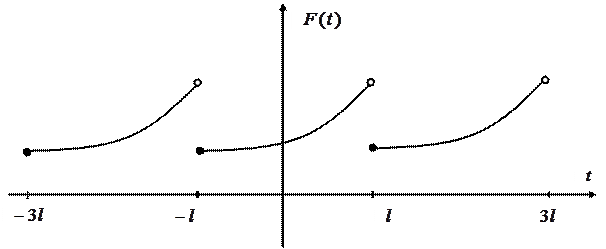
Рисунок 2.8
Одержана періодична функція 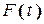 задовольняє умови теореми 1
задовольняє умови теореми 1 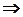 вона розкладається в ряд Фур’є. Але на
вона розкладається в ряд Фур’є. Але на 
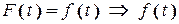 розкладається в ряд Фур’є (2.5).
розкладається в ряд Фур’є (2.5).
Розкладання в ряд Фур’є функцій, які задані на 
Нехай функція, що задана на  (див. рисунок 2.9), є кусково гладкою на
(див. рисунок 2.9), є кусково гладкою на  .
.
 |
Рисунок 2.9
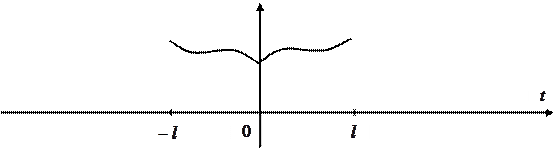 Спочатку продовжимо її парним чином на
Спочатку продовжимо її парним чином на  (див. рисунок 2.10),
(див. рисунок 2.10),
Рисунок 2.10
а потім періодично на всю вісь (див. рисунок 2.11)
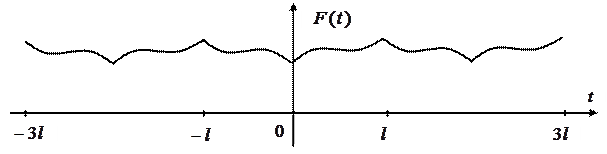 |
Рисунок 2.11
Одержана періодична парна функція 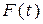 задовольняє умови теореми 1
задовольняє умови теореми 1 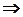 вона розкладається в ряд Фур’є (2.13) по косинусах. Але на
вона розкладається в ряд Фур’є (2.13) по косинусах. Але на 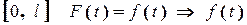 при
при 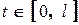 розкладається в ряд Фур’є (2.13) по косинусах.
розкладається в ряд Фур’є (2.13) по косинусах.
Аналогічно, продовжуючи 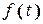 непарним чином на
непарним чином на  (див. рисунок 2.12),
(див. рисунок 2.12),
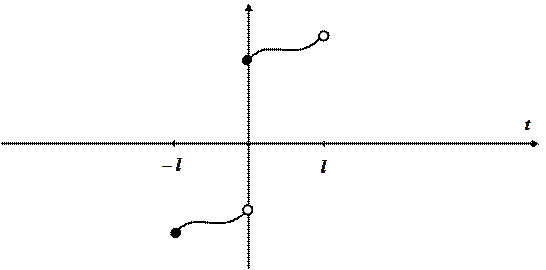 |
Рисунок 2.12
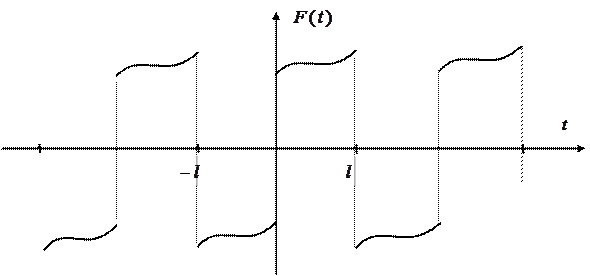 а потім періодично на всю вісь (див. рисунок 2.13),
а потім періодично на всю вісь (див. рисунок 2.13),
Рисунок 2.13
бачимо, що 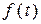 розкладається в ряд Фур’є (2.14) по синусах.
розкладається в ряд Фур’є (2.14) по синусах.
ЗАВДАННЯ
Періодичний сигнал 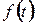 задано на періоді
задано на періоді 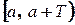 (див. рисунок 2.14).
(див. рисунок 2.14).
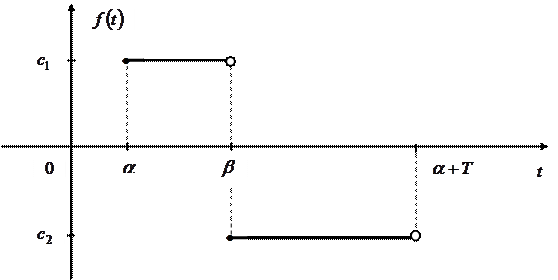 |
Рисунок 2.14
1 Зобразити графік 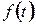 на відрізку
на відрізку 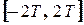 .
.
2 Розкласти 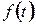 в ряд Фур’є в дійсній формі.
в ряд Фур’є в дійсній формі.
3 Знайти амплітудний та фазовий спектри сигналу 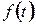 , обмежуючись першими п’ятьма частотами, починаючи з
, обмежуючись першими п’ятьма частотами, починаючи з 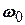 .
.
4 Знайти значення суми ряду в точках 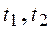 і порівняти ці значення зі значеннями суми перших п’яти членів ряду Фур’є.
і порівняти ці значення зі значеннями суми перших п’яти членів ряду Фур’є.
5 Вважаючи, що 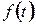 - струм у провіднику з опором
- струм у провіднику з опором 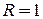 , знайти з допомогою рівності Парсеваля сумарну середню за період потужність гармонічних складових цього струму, починаючи зі складової, що відповідає частоті
, знайти з допомогою рівності Парсеваля сумарну середню за період потужність гармонічних складових цього струму, починаючи зі складової, що відповідає частоті 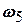 .
.
6 Записати одержаний ряд Фур’є в комплексній формі.
Таблиця 2.1
| № | a | b | Т | С1 | С2 | t1 | t2 |
| -1 | –2 | ||||||
| -2 | –3 | ||||||
| -1 | –3 | ||||||
| ½ | 3/2 | -2 | –1/2 | ||||
| -2 | -1 | -3 | -1 | ||||
| -1 | -2 | –7 | |||||
| 1/3 | 2/3 | -1 | –2/3 | 5/3 | |||
| 5/2 | -4 | -2 | –2 | ||||
| -2 | -3 |
Продовження таблиці 2.1
| -1/2 | 3/2 | ||||||
| -6 | -4 | -2 | |||||
| -3 | -2 | –2 | |||||
| -1 | -1 | –5 | 5/2 | ||||
| 1/2 | |||||||
| -1/2 | -1 | -5 | 3/2 | ||||
| -1 | –3 | ||||||
| -1 | -4 | –3 | |||||
| -2 | –2 | ||||||
| -2 | -1 | -4 | -5 | - | |||
| –2 | |||||||
| -4/5 | 3/5 | -3 | –9/5 | 11/5 | |||
| -5 | –4 | –3 | |||||
| -2 | -1 | -2 | -1 | –5 | |||
| -3/2 | -1/2 | 3/2 | |||||
| -5 | -4 | –8 | |||||
| -1 | -3 | ||||||
| -4 | -2 | ||||||
| 5/2 | -3 | 1/2 | 7/2 | ||||
| 1/2 | 3/2 | -2 | –3/2 | ||||
| -4 | -1 | -4 | |||||
| -2 | -2 | ||||||
| -2 |
Розв’язання № 31. В цьому випадку:
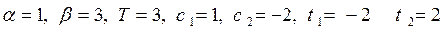 ,
,
тобто на 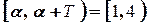 сигнал має вигляд (див. рисунок 2.15):
сигнал має вигляд (див. рисунок 2.15):
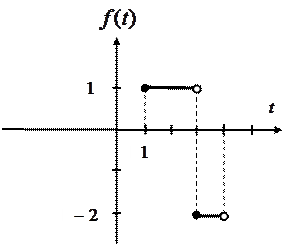 |
Рисунок 2.15
1 Зображуємо сигнал на 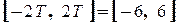 (див. рисунок 2.16):
(див. рисунок 2.16):
 2
2
Рисунок 2.16

 3
3 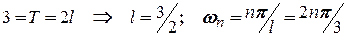 . Для того, щоб спростити обчислення коефіцієнтів Фур’є, розглянемо сигнал
. Для того, щоб спростити обчислення коефіцієнтів Фур’є, розглянемо сигнал 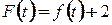 (див. рисунок 2.17):
(див. рисунок 2.17):
Рисунок 2.17
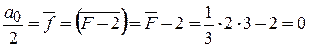 .
.
Оскільки 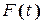 відрізняється від
відрізняється від 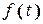 на сталу складову, то їх коефіцієнти Фур’є при
на сталу складову, то їх коефіцієнти Фур’є при 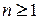 співпадають. Тому, використовуючи властивість 3 періодичних функцій, маємо:
співпадають. Тому, використовуючи властивість 3 періодичних функцій, маємо:
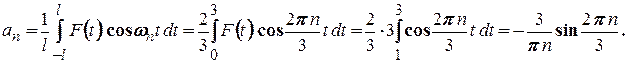
Аналогічно
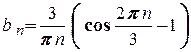 .
.
Отже, розвинення 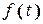 в ряд Фур’є має вигляд:
в ряд Фур’є має вигляд:
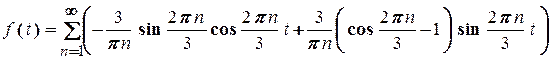 . (2.15)
. (2.15)
4 Стала складова дорівнює нулю.
Перша гармоніка:
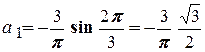 ,
,  ;
;
і тому
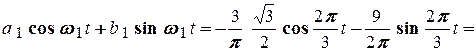
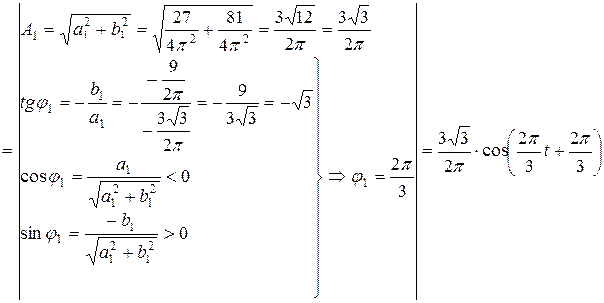 .
.
Друга гармоніка:
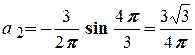 ,
, 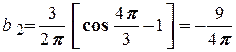 .
.
і тому
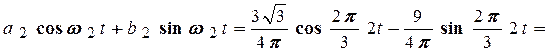
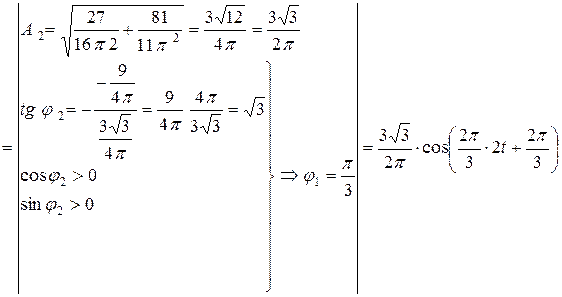 .
.
Третя гармоніка дорівнює нулю, оскільки:
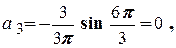
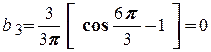 .
.
Четверта гармоніка:
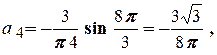
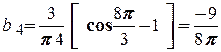 ;
;
і тому
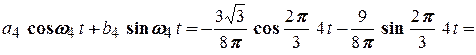
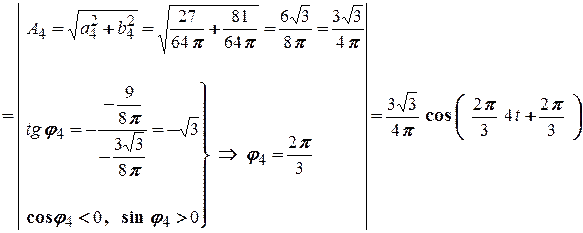 .
.
Зображуємо амплітудний і фазовий спектри, обмежуючись першими п’ятьма частотами (див. рисунок 2.18):
 |
Рисунок 2.18
4 Згідно з теоремою 1 сума ряду 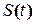 ряду Фур’є (2.15) в точках
ряду Фур’є (2.15) в точках 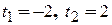 дорівнює відповідно:
дорівнює відповідно:
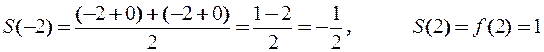 .
.
А сума перших п’яти гармонік в цих же точках має значення відповідно:
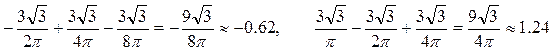 ,
,
які мало відрізняються від S(–2) і S(2) відповідно (що свідчить про те, що пункти 2,3 завдання виконані вірно).
5 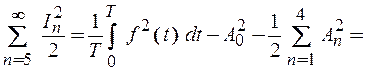
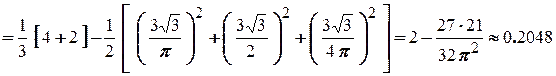 .
.
6 При n ³ 1
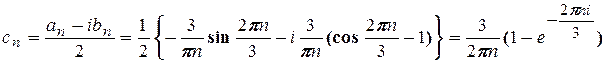 ,
,
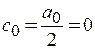 ,
, 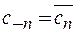 (оскільки сигнал
(оскільки сигнал  дійсний). Тому комплексна форма ряду Фур’є (2.15) має вигляд
дійсний). Тому комплексна форма ряду Фур’є (2.15) має вигляд
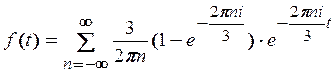 .
.
Наостанок наведемо звіт про виконання варіанта № 32, який склала студентка Т. І. Лобода, використовуючи Mathcad, при цьому перелік завдань дещо модифіковано з урахуванням того, що при їх виконанні використовувалась ПЕОМ.
Дата добавления: 2015-11-04; просмотров: 1852;
