Истечение газов и паров
Если в цилиндре А (рис. 7.1) с насадкой С находится газ под давлением более высоким, чем давление окружающей среды, то через эту насадку будет происходить истечение заключенного в цилиндре газа наружу.
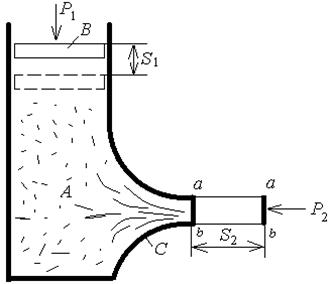
Рис. 7.1. Истечение газа из сопла
При этом оказывается, что по мере движения по насадке давление газа постепенно понижается, а скорость – возрастает, т.е. происходит превращение потенциальной энергии в кинетическую. Такие насадки, в которых происходит преобразование потенциальной энергии протекающего по ним газа в кинетическую, называются соплами.
При некоторых условиях, когда к насадке подводится газ с большой скоростью, может происходить обратный процесс, при котором скорость газа по мере движения по насадке постепенно уменьшается, а давление его увеличивается, т. е. происходит преобразование кинетической энергии в потенциальную. Такие насадки называют диффузорами.
Рассмотрим сначала процесс истечения газа через суживающееся сопло из цилиндра А ( рис. 7.1), в котором поддерживается постоянное давление Р1 – большее, чем давление Р2 окружающей среды.
Допустим, что перед истечением газ находился в состоянии покоя, а в процессе истечения пришел в движение и приобрел в сечении ab скорость w. В этом случае потенциальная энергия газа перешла в кинетическую, равную 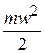 , где m – масса вытекающего газа. Допустим также для простоты, что количество вытекающего из сопла газа равно 1 кг, при этом
, где m – масса вытекающего газа. Допустим также для простоты, что количество вытекающего из сопла газа равно 1 кг, при этом 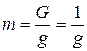 и кинетическая энергия вытекающей струи в сечении ab будет, очевидно,
и кинетическая энергия вытекающей струи в сечении ab будет, очевидно, 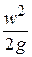 .
.
При вытекании из цилиндра 1 кг газа поршень В опустился на величину s1 м. Величина совершенной при этом работы выталкивания
l1 = P1 f1 s1 кгс·м/кг,
где f1 – площадь поршня В. Но произведение f1 × s1 = v1 – удельному объему газа в цилиндре, поэтому
l1 = P1 · v1 кгс·м/кг.
Так как наружная среда, в которую происходит истечение, имеет давление Р2, то вытекающий из сопла газ должен преодолевать силу, противодействующую истечению и равную P2 × f2, где f2 – площадь выходного отверстия сопла. На преодоление этой силы должна быть затрачена часть работы l1, равная l2 = P2 × f2 s2 = P2 · v2, где v2 – удельный объем в сечении ab.
При движении газа по соплу от сечения mn до сечения ab (рис. 7.2) давление понизилось от P1 до P2, а удельный объем увеличился от v1 до v2. Таким образом, газ совершил некоторый процесс АВ, в котором была произведена работа расширения l3.
Таким образом, полная работа истечения 1 кг газа
l0 = l1 – l2 + l3 кгс·м/кг. 
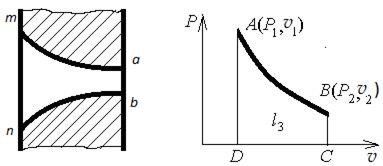
Рис. 7.2. Изображение в осях vP процесса истечения газа через
суживающееся сопло. Здесь P1 – давление газа при входе в сопло,
а P2 – при выходе из него
Вследствие большой скорости истечения время прохождения газа по соплу весьма мало. Поэтому можно считать, что теплообмен между газом и внешней средой через стенки сопла не происходит, и процесс истечения является адиабатным. При этом работа расширения может быть выражена уравнением:
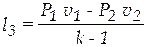 ,
,
где k – показатель адиабаты (для перегретого пара k = 1,3).
Имея в виду полученные выше значения для l1 и l2, можем написать, что
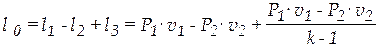 .
.
или
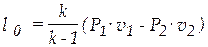 .
.
Скорость течения газа из сопла и расход газа увеличиваются с уменьшением отношения 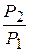 , например, с уменьшением давления
, например, с уменьшением давления 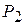 на выходе из сопла при постоянном
на выходе из сопла при постоянном 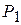 . Опытом было установлено, что если сопло по форме суживающееся (рис. 7.2), то давление
. Опытом было установлено, что если сопло по форме суживающееся (рис. 7.2), то давление 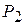 в сечении ab может уменьшаться только до известного предела, называемого критическим давлением
в сечении ab может уменьшаться только до известного предела, называемого критическим давлением 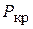 .
.
Дата добавления: 2015-09-07; просмотров: 1494;
