Вопрос 1. Понятие эластичности спроса и предложения.

Тема 2.2 Эластичность спроса и предложения.

Вопрос 1. Понятие эластичности спроса и предложения.

Вопрос 2. Виды эластичности.

Вопрос 3. Факторы эластичности.

Вопрос 1. Понятие эластичности спроса и предложения.

При проведении экономических расчетов, и особенно при прогнозировании различных важных для производителей и потребителей процессов, очень часто возникает необходимость не просто определить общий вид функций спроса и предложения, но и выяснить, как сильно будет реагировать в каждом данном конкретном случае величина спроса или предложения на изменения соответствующих факторов, другими словами, насколько значительными окажутся при этом ее ответные изменения. Ведь цель построения всякой модели — описание взаимосвязей между экономическими переменными, позволяющее объяснять и предсказывать, как изменения какого-либо фактора влияют на другие экономические переменные. Здесь важно выяснить, насколько чувствителен исследуемый экономический показатель к изменению определяющих его факторов. Очевидно, что для этого не всегда будет достаточно сопоставить приросты (абсолютные изменения), скажем, величины предложения и цены данного товара. (Напомним, что когда величина Q меняется от значения Q0 (начальное значение) до значения Q1 (конечное значение), то величина DQ = Ql — Q0 называется абсолютным изменением (приращением) величины Q.)

Во-первых, абсолютные изменения будут зависеть от совсем не относящихся к сути дела причин, например, от выбора единицы измерения объемов товара и цен. Во-вторых, такие соотношения приростов нельзя будет сравнивать, если они будут относиться к разным товарам, из-за несовпадения их размерностей. В-третьих, что еще существеннее, для разных товаров и разных условий одни и те же абсолютные изменения могут иметь совершенно различный смысл. Так, рост цены на 10 000 рублей будет означать совсем разные вещи для карандаша и для пишущей машинки, а рост объема спроса на 100 штук — для порций мороженого и для атомных подводных лодок. Решающее значение для определения того, насколько существенны данные изменения, например, количества товара или цены, будут иметь сами исходные размеры данных величин.

Поэтому от абсолютных изменений сопоставляемых при анализе величин необходимо перейти к относительным: в нашем примере от AQ к AQ / Q. А темп прироста (процентное изменение) какой-либо величины — это измеренное в процентах отношение приращения этой величины к первоначальному ее значению:

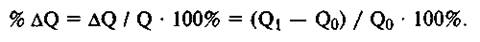
Это позволит разрешить только что указанные проблемы: единица и масштаб измерения потеряют значение, так как в числителе и знаменателе таких дробей они будут одинаковыми; сопоставимость по различным товарам будет обеспечена безразмерностью относительных изменений, выражаемых в долях от базовых величин или в процентах; наконец, степень значимости таких изменений можно будет установить исходя из соотношений полученных таким образом относительных величин. Итак, чувствительность одного фактора к поведению другого лучше всего определять исходя не только из абсолютных, но и из относительных изменений их обоих.

Точно так же имеются два подхода к анализу чувствительности зависимости, представленной функцией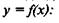

1) приростный подход: как меняется значение функции у при изменении независимой переменной х на единицу. Этот подход позволяет рассматривать связи типа:

прирост фактора (Ах) => прирост исследуемого показателя (Ау).

Меру "абсолютной" чувствительности можно назвать скоростью изменения функции. Мера чувствительности функции в данной точке ("мгновенная скорость") называется производной;

2) темповый подход: на сколько процентов изменится значение функции при изменении независимой переменной на один процент. Этот подход позволяет рассматривать связи типа:

темп прироста фактора (%(х) => => темп прироста исследуемого показателя (%(у).

Вспомним характеристику производной. Пусть дана функция 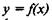и

два значения аргумента, хо и x1. Им соответствуют два значения функции, 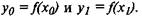Разность 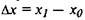является приращением аргумента, а

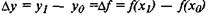— приращением функции. Геометрическая интерпретация этих величин показана на рис. 8.1.

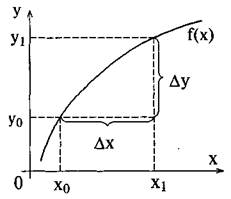
Рис. 8.1

Мы можем измерить степень абсолютной чувствительности переменной у к изменениям переменной х, если определим соотношение 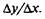Недостаток такого определения чувствительности состоит в том, что она зависит не только от "начальной" точки хо, относительно которой рассматривается изменение аргумента, но и от самой величины интервала Dx, на котором определяется скорость. Для устранения этого недостатка вводится понятие производной (скорости изменения функции в точке). При определении скорости изменения функции в точке сближают точки xq и xj, устремляя интервал Ах к нулю. Скорость изменения функции f(x) в точке xq и называют производной функции f(x) в точке Хо- Геометрический смысл скорости изменения функции в точке хо в том, что она определяется углом наклона касательной к графику функции в точке xq. Производная — это тангенс угла наклона касательной к графику функции.

Производную функции 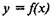в точке х обозначают f'(x) ("эф штрих от икс"), у'х ("игрек штрих по икс"), 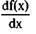("де эф по де икс"), 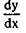("де игрек по де икс"), причем все эти обозначения равноправны. Операция нахождения производной называется дифференцированием функции.

Тем не менее использование производной как меры чувствительности функции связи экономических переменных не всегда удобно по указанным выше соображениям. Например, если мы рассмотрим функцию спроса на сахар (QD) от его цены (Р), то увидим, что значение производной при каждой цене Р (измеряемой в рублях) зависит от того, измеряется ли спрос на сахар в килограммах или в центнерах. В первом случае производная измеряется в кг/руб., во втором — в ц/руб. Кроме того, производная связывает абсолютные, а не относительные изменения функции и аргумента. Поэтому для измерения чувствительности изменения функции к изменению аргумента в экономике часто изучают связь не абсолютных изменений переменных х и у, а их относительных изменений.

Для этих целей и используется показатель эластичности, введенный в экономический анализ А.Маршаллом. Эластичностью данной величины можно считать измеряемую в относительной форме степень изменения ее значения в ответ на изменение значения другой сопоставляемой с ней при анализе величины. В аналитическом выражении эластичность ( величины спроса Q по цене Р (или просто ценовая эластичность спроса) может быть найдена исходя из соотношения относительных изменений объема спроса и цены:

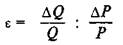
или после упрощений

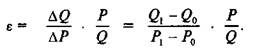
При исследовании чувствительности находящихся в функциональны)! зависимостях сопоставляемых величин используют эластичности функций.

Эластичность функции у =f(x) показывает относительное изменение значения функции у в расчете на единицу относительного изменения аргумента х. Если эластичность переменной у по переменной х обозначить ехО0, то, используя определение эластичности, получаем:

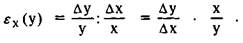
Учитывая, что при 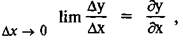(то есть, при малых при-

ращениях аргумента отношение приращений Ау и Ах приближается к производной у по х), имеем:

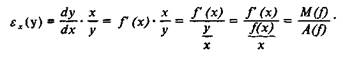
Если f(x) считать общей (совокупной) величиной (как, например, общая или совокупная выручка), то М ф = Ау/Лх — соответствующая ей предельная величина (например, предельная выручка, или дополнительная выручка (у от дополнительной единицы (х), а А ф — средняя величина (средняя выручка, или выручка в среднем на единицу х, равная у/х, в нашем примере это — цена). Итак, эластичность функции равна отношению предельной и средней величин.

Если вспомнить, что в соответствии с законом спроса изменения величины спроса и цены данного товара разнонаправлены, станет понятным, что коэффициент ценовой эластичности спроса должен быть отрицательным. Для простоты анализа знак "минус" иногда опускают. Фактически при этом имеют дело с абсолютным значением или попросту модулем коэффициента эластичности |б|.

Абсолютное значение коэффициента эластичности может изменяться в диапазоне от нуля до бесконечности, однако важной границей является единица, поскольку она разделяет реакцию, превышающую исходный импульс, и менее чувствительные ответные изменения. При |е| < 1 степень изменения, например, объема спроса меньше исходного изменения цены — значит, мы имеем дело с товаром неэластичного (жесткого) спроса. При единичной эластичности (|б| =1) исходный импульс и ответная реакция совпадают по относительной величине. Если же |е| > 1, то можно говорить о товаре эластичного (гибкого) спроса. Крайними случаями являются: с одной стороны, нулевая эластичность (рис. 8.2).

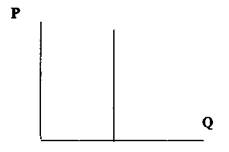
Рис. 8.2

В этом случае кривая спроса (или предложения) строго вертикальна: AQ = 0 при любых изменениях цены, т. е. величина спроса или предложения совсем не реагирует на изменения цены.

С другой стороны, это бесконечная эластичность (рис. 8.3).

Рис. 8.3

В этом случае кривая спроса (или предложения) строго горизонтальна: 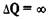при самых незначительных изменениях цены, то есть объем спроса или предложения при малейшем соответственном росте или падении цены снизится до 0.

Кривые же спроса и предложения с постоянной эластичностью — это графики степенных функций. Для спроса это — гипербола:

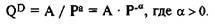
Тогда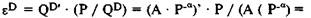

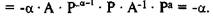Кстати, отсюда следует, что кривая спроса с единичной эластичностью — это гипербола с показателем степени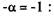

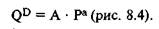
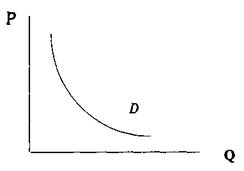
Рис. 8.4

Для предложения: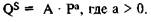

Тогда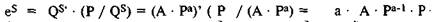

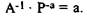Отсюда следует, что кривая предложения с единичной эластичностью — это график линейной функции, выходящей из начала координат: 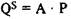(рис. 8.5).

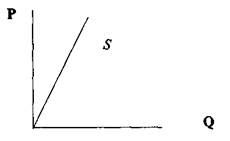
Рис. 8.5

Эластичность спроса — это степень изменения величины спроса от изменения цены или других факторов.

Эластичность предложения по цене характеризует степень изменения объема предложения в зависимости от изменения цены.