Силы в зацеплении прямозубых передач
Силы взаимодействия между зубьями принято определять в полюсе зацепления П (4.1).

Рис. 4.1 Схема сил в прямозубой цилиндрической передаче
Распределенную по контактным линиям нагрузку в зацеплении заменяют равнодействующей Fn , которая направлена по линии давления (зацепления) NN. Силами трения в зацеплении пренебрегают, так как они малы. Для расчета зубьев, валов и опор силу Fn раскладывают на составляющие:
окружная сила
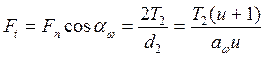 (4.6)
(4.6)
Радиальная сила
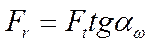 (4.7)
(4.7)
Где Т2 – вращающий момент на колесе; Ft =20° – угол зацепления.
На ведомом колесе направление силы Ft совпадает с направлением вращения, на ведущем – противоположно ему.
ГЛАВА 5. ЦИЛИНДРИЧЕСКИЕ КОСОЗУБЫЕ ПЕРЕДАЧИ
Общие сведения
Цилиндрические колеса, у которых зубья расположены по винтовым линиям на делительном цилиндре, называют к о с о з у б ы м и. В отличие от прямозубой в косозубой передаче зубья входят в зацепление не сразу по всей длине, а постепенно. Увеличивается время контакта одной пары зубьев, в течение которого входят новые пары зубьев, нагрузка передается но большому числу контактных линий, что значительно снижает шум и динамические нагрузки.
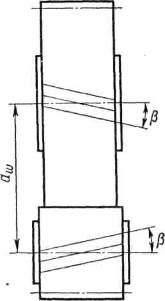
Чем больше угол наклона линии зуба β (рис. 5.1), тем выше плавность зацепления. У пары сопряженных косозубых колес
|
|
Рис. 5.1 Косозубая передача
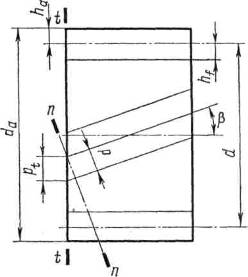
Рис. 5.2 Геометрические размеры косозубого колеса
с внешним зацеплением углы β равны, но противоположны по направлению.
Если к передачам не предъявляют специальных требований, то колеса нарезают правыми, а шестерни— левыми.
У косозубого колеса (рис. 5.2) расстояние между зубьями можно измерить в торцовом, или окружном (t—t), и нормальном (п — п) направлениях. В первом случае получим окружной шаг pt, во втором — нормальный шаг р. Различными в этих направлениях будут и модули зацепления:
mt = pt/л; m = р/л,
где mt и m — окружной и нормальный модули зубьев. Согласно рис. 5.2
pt = P/cos β,
следовательно,
mt = m/cos β,
где β — угол наклона зуба на делительном цилиндре.
Нормальный модульmдолжен соответствовать стандарту и являться исходной величиной при геометрических расчетах.
Делительный и начальный диаметры
(5.1)
d=dw=mtz = mz/cosβ.
Косозубое колесо нарезают тем же инструментом, что и прямозубые. Наклон зуба получают поворотом инструмента на угол р. Профиль косого зуба в нормальном сечениисоответствует исходному контуру инструментальной рейки и, следовательно, совпадает спрофилем прямого зуба модуля т.
Высоты головки косого зуба hаи ножки hf соответственно равны:
ha = m; hf = 1,25m. (5.2)
Диаметр вершин
da = d + 2m. (5.3)
Межосевое расстояние
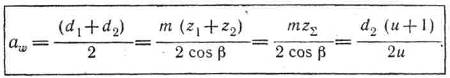
|
(5.4)
В косозубой передаче, меняя значение угла β, можно незначительно изменить aw.
Из формулы (5.5) следует, что с увеличением β возрастает zv.
Силы в зацеплении
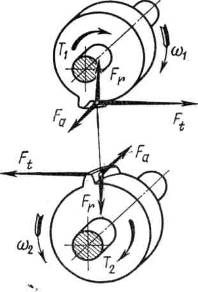
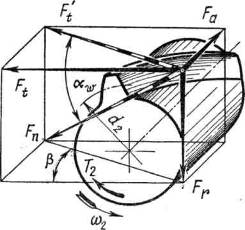
Вкосозубой передаче нормальная сила Fnсоставляет угол β с торцом колеса (рис. 5.4). Разложив Fnна составляющие, получим:
радиальную силу
(5.6)
Fr = Ft tg αw/COS β
где Ft = 2T2/d2 — окружная сила;
осевую силу
Fa = Fttg β
(5.7)
При определении направлений сил учитывают направление вращения колес и направление наклона зуба (правое или левое).
|
|
Рис. 5.4. Схема сил в косозубой передаче
Осевая сила Fa дополнительно нагружает подшипники, возрастая с увеличениемβ. По этой причине для косозубых колес принимаютβ = 8... 18°. Наличие в зацеплении осевых сил является недостатком косозубой передачи.
Дата добавления: 2015-10-26; просмотров: 14808;
