Расчет средней процентной ставки

В условиях нестабильности финансового рынка процентные ставки могут быть непостоянны во времени. В связи с этим возникает задача определения такого значения процентной ставки, которое определяло бы уровень доходности за весь период финансовой операции. Для решения этой задачи определяют среднюю процентную ставку с помощью уравнения эквивалентности, которое ставит в соответствие коэффициенту наращения, определенному на основе годовой процентной ставки последовательность коэффициентов наращения, задающих схему проведения данной финансовой операции.

а) Предположим, что в течение периода времени 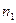установлена ставка простых процентов 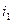, в течение периода времени 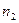действует ставка простых процентов 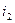и т.д. Всего число периодов начисления процентов - 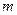. В этом случае срок финансовой операции определяется суммой: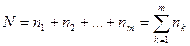

Обозначим процентную ставку ссудных процентов, характеризующую среднюю доходность за конверсионный период, символом 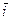. Тогда уравнение эквивалентности для ее определения будет иметь вид:

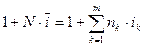
Отсюда

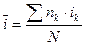(5.4)

Аналогично для простых учетных ставок 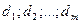их средняя определяется из равенства: 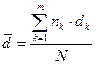. (5.5)

Средняя ставка 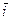(равно как и 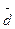) — это взвешенная средняя арифметическая величина, при расчете которой каждому значению процентной ставки ставится в соответствие интервал, в течение которого данное значение ставки использовалось.

В общем виде определение средней ставки может быть сформулировано следующим образом.

Средняя процентная ставка — это ставка, дающая такое наращение, которое эквивалентно наращению с применением ряда разных по значению процентных ставок, применяемых на различных интервалах времени.

Пример. На долг в 400 000 рублей согласно контракту предусматривается начислить годовые простые точные проценты по схеме, определенной следующей таблицей.

Таблица

Период
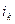
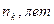
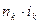
	0,12	0,75	0,09
	0,11	2,0	0,22
	0,08	1,25	0,1
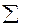
		4,0	0,41

Требуется оценить доходность этой кредитной операции в виде простой годовой процентной ставки и найти сумму долга с процентами.

Решение: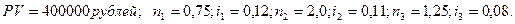

Срок финансовой операции:

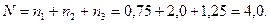
Средняя процентная ставка:

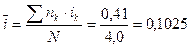
или 10,25 % годовых.

Сумма долга с процентами:

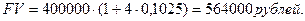
б) Допустим, что доходность операции с плавающей процентной ставкой на каждом интервале начисления была выражена через сложный процент. В этом случае средняя процентная ставка, которая равноценна последовательности ставок за весь период финансовой операции, может быть получена из следующего уравнения эквивалентности: .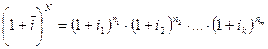

Отсюда 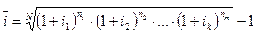, (5.6)

где

.

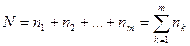Следовательно, сложная средняя процентная ставка рассчитывается по формуле средней геометрической взвешенной.

Пример. Сложная процентная ставка по ссуде определена на уровне 8,5 % плюс маржа 0,5 % в первые 2 года и 0,75 % в последующие 3 года. Требуется определить среднюю ставку сложных процентов.

Решение:

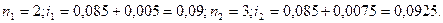
Срок финансовой операции: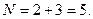

Средняя ставка сложных процентов: 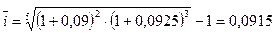или 9,15% годовых.