Решение. Разложим силу Р на составляющие по на­правлениям главных центральных осей сечения:

Разложим силу Р на составляющие по на­правлениям главных центральных осей сечения:

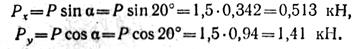
Наибольшие изгибающие моменты от каждой из состав­ляющих сил возникнут в защемленном сечении:

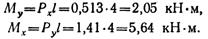
Наибольшие напряжения будут в точках А и С; в точке А — растягивающие, в точке С — сжимающие. По абсолютному значению они равны.

Составим условие прочности для точки А, учитывая, что W_x = bh²/6, a W_y = hb²/6:

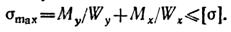
Подставим числовые значения:

Откуда

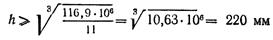
и, следовательно,

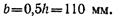
Пример 10. Определить необходимый по условию прочности диаметр поперечного сечения стержня, изгибае­мого силами, действующими в двух взаимно перпендику­лярных плоскостях (рис. 2.65, а). Допускаемое напряже­ние [σ] =130 Н/мм².