Решение. Поместим начало координат на опоре A
Поместим начало координат на опоре A. Разобьем балку на два участка и составим обобщенные уравнения упругой линии и углов поворота для каждого из них, предварительно определив опорные реакции:
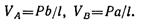
для первого участка
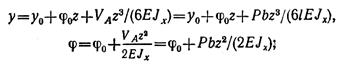
для второго участка
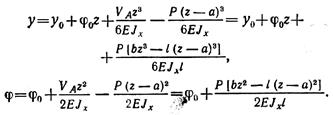
Определяем начальные параметры исходя из условий опорных закреплений:
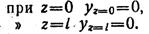
Из первого уравнения находим у0:
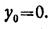
Из уравнения прогибов для второго участка находим угол поворота φ0 сечения на левой опоре:
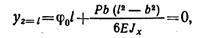
Откуда
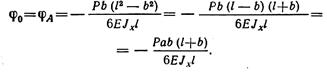
Подставив значение φ0 в уравнение прогибов первого участка, получим
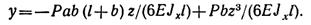
При z = a найдем прогиб сечения под точкой приложения силы Р:
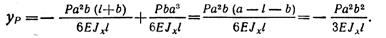
Используя уравнение углов поворота для второго участка
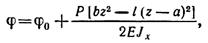
найдем при z = l угол поворота сечения на правой опоре В:
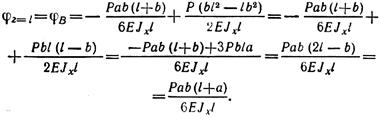
Угол поворота φВ положителен, следовательно, он в отличие от угла поворота φА направлен против часовой стрелки.
При приложении силы Р посередине пролета балки, т. е. при а = b = l/2, углы поворота опорных сечений и прогиб под точкой приложения силы примут значения:
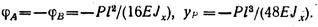
Пример 5. Определить максимальный прогиб двухопорной балки, нагруженной равномерно распределенной по всему пролету нагрузкой интенсивностью q и сосредоточенной силой Р посередине пролета.
Дата добавления: 2015-09-07; просмотров: 607;
