Решение. 1. Определяем моменты пар сил на шкивах.
1. Определяем моменты пар сил на шкивах.
Вращающий момент определяем из формулы мощности при вращательном движении
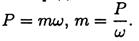
Момент на шкиве 1 движущий, а моменты на шкивах 2, 3, 4 — моменты сопротивления механизмов, поэтому они имеют противоположное направление. Брус скручивается между движущим моментом и моментами сопротивления. При равновесии момент движущий равен сумме моментов сопротивления:
2. Определяем крутящие моменты в поперечных сечениях бруса с помощью метода сечений.
 |
3. Строим эпюру крутящих моментов. Заметим, что скачок на эпюре всегда численно равен приложенному вращающему моменту.
Выбираем соответствующий масштаб.
Откладываем значения моментов, штрихуем эпюру поперек, обводим по контуру, записываем значения моментов (см. эпюру под схемой вала (рис. 26.3)). Максимальный крутящий момент на участке III Мкз = 320 Н*м.
Пример 2. Выбрать рациональное расположение колес на валу (рис. 26.5). m1 = 280 Н • м; т2 = 140 Н • м; т3 = 80 Н* м.
Примечание. Меняя местами колеса (шкивы) на валу, можно изменять величины крутящих моментов. Рациональным расположением является такое, при котором крутящие моменты принимают минимальные из возможных значения.
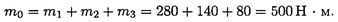
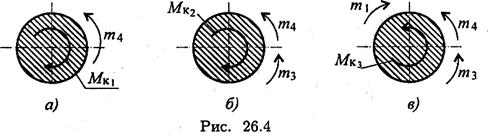
Рассмотрим нагрузки на валу при различном расположении колес.
Из представленных вариантов наиболее рационально расположение шкивов в третьем случае, здесь значения крутящих моментов минимальны. Вывод: при установке шкивов желательно, чтобы мощность подавалась в середине вала и по возможности равномерно распределялась направо и налево.
Пример 3. Для бруса, изображенного на рис. 2.34, а, построить эпюру крутящих моментов.
Решение
1. Заданный брус имеет три участка I, II, III. Напомним, что границами участков являются сечения, в которых прилажены внешние (скручивающие) моменты.
В данном случае проще, применяя метод сечений, оставлять левую и отбрасывать правую часть бруса — это дает возможность не определять реактивный момент в заделке.
Проводим произвольное поперечное сечение на участке I и составляем уравнение равновесия для оставленной части бруса, изображенной отдельно на рис. 2.34, 6:
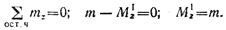
В любом сечении участка I крутящий момент имеет найденное значение M1z = т. Из уравнения равновесия для оставленной части значение M1z получилось со знаком плюс. Это указывает на то, что выбранное направление M1z соответствует действительному.
Эпюра крутящих моментов на этом участке — прямая, параллельная оси абсцисс. Согласно принятому правилу знаков М1я отрицателен, и ординаты эпюры откладываем вниз от ее оси.
2. Проводим произвольное поперечное сечение на участке II и составляем уравнение равновесия для оставленной части бруса, изображенной отдельно на рис. 2.34, в:
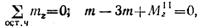
Откуда
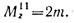
И в этом случае выбранное направление MIIz соответствует действительному. В любом сечении участка II крутящий момент MzII = 2m. Согласно принятому правилу знаков, MzII положителен и ординаты эпюры откладываем вверх от ее оси.
3. Проводим произвольное поперечное сечение на участке III и составляем уравнение равновесия для оставленной части бруса, изображенной отдельно на рис. 2.34, г:
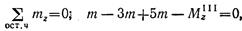
откуда
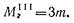
В любом сечении участка III MzIII = —Зт.
Эпюра крутящих моментов представлена на рис. 2.34, д.
При нагружении бруса сосредоточенными моментами эпюра всегда имеет такой же характер, как и в рассматриваемом случае: на отдельных участках она ограничена прямыми, параллельными оси абсцисс; в местах приложения внешних (скручивающих) моментов получаются скачки на величину этих моментов.
Пример 4. На вал насажены шкивы 1, 2, 3, 4 (рис. 2.35, а). Шкив 1 передает от источника энергии на вал мощность N1 = 5,2 кВт, а остальные шкивы снимают с вала и передают рабочим машинам мощности соответственно N2 = 1,5 кВт; N3 = 1,7 кВт; N4 = 2,0 кВт. Вал вращается с частотой п = 240 об/мин. Построить эпюру крутящих моментов.
Дата добавления: 2015-09-07; просмотров: 711;