Решение. Найдем сумму арифметической прогрессии
Найдем сумму арифметической прогрессии
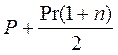при Р=5000; r=0,1; n=5:
5000+5000∙0.1(1+5) / 2=6500
Сумма ежегодных выплат представлена в таблице.
| Год | ||||||
| Основной долг | ||||||
| Проценты | ||||||
| Сумма к выплате |
Пусть заем в сумме Р выдан под r сложных ссудных процентов на n периодов. При погашении займа равными годовыми выплатами ежегодные платежи можно рассматривать как годовую ренту (аннуитет) с продолжительностью n периодов и неизвестным платежом, равным А. Неизвестный платеж ренты можно найти, приравнивая современную стоимость этой ренты сумме займа.
Тогда платеж А находим из уравнения: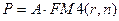 
, поэтому
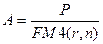
Общая сумма выплат при этом составит величину n×A
Дата добавления: 2015-10-19; просмотров: 601;