Логические основы ЭВМ

Для анализа и синтеза схем в ЭВМ при алгоритмизации и программировании решения задач широко используется математический аппарат алгебры логики. Основоположником математической логики является немецкий математик Готфрид Вильгельм Лейбниц (1646-1716 гг.). На заложенном Лейбницем фундаменте ирландский математик Джордж Буль построил здание новой науки – математической логики, которая в отличие от обычной алгебры оперирует не числами, а высказываниями.

Алгебра логики – это раздел математической логики, значения всех элементов (функций и аргументов) которой определены в двухэлементном множестве: 0 и 1.

Пример 9. Определить значения истинности для следующих высказываний.

«Лед – твердое вещество» - истинное высказывание.

«Париж – столица Китая» - ложное высказывание.

«Треугольник – это геометрическая фигура» - истинное высказывание.

Таким образом, по своей сути высказывания фактически являются двоичными объектами и поэтому истинному значению ставят в соответствии 1 (TRUE), а ложному – 0 (FALSE). В алгебре логики все высказывания обозначают буквами А, B, C и т.д. Например, запись А = 1 означает, что высказывание А истинно.

Высказывания могут быть простыми и сложными. Простые соответствуют алгебраическим переменным, а сложные являются аналогом алгебраических функций. Функции могут получаться путем объединения переменных с помощью логических операций.

Простейшими операциями в алгебре логики являются следующие операции:

§ Логическое сложение (операция ИЛИ (OR), операция дизъюнкции)

Это бинарная операция, так как представляет собой результат действий над двумя логическими величинами. Записывается в виде: AÚBилиA+B. Значение такого выражения будет ИСТИНА, если значение хотя бы одного из операндов истинно.

§ Логическое умножение (операция И (AND), операция конъюнкции)

Также является бинарной, но в отличии от дизъюнкции имеет значение ИСТИНА, если оба ее операнда истинны. Записывается:AÙBилиA*B.

§ Отрицание (операция НЕ (NOT), операция инверсии)

Унарная операция, то есть имеет всего один операнд. Записывается: 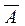или Ø A.

Операции И, ИЛИ, НЕ образуют полную систему логических операций, из которых можно построить сколь угодно сложное логическое выражение.

Логическое выражение (логическая формула) – формула, содержащая лишь логические величины и знаки логических операций. Результатом вычисления логической формулы является одно из двух значений: ИСТИНА или ЛОЖЬ.

Последовательность выполнения операций в логических формулах определяется старшинством операций. В порядке убывания старшинства логические операции расположены так: отрицание, конъюнкция, дизъюнкция.

 

Существуют специальные таблицы, в которых указываются все возможные комбинации логических переменных A и B, а также соответствующие им результаты операций. Они называются таблицами истинности.

Таблицы истинности:

A	NOT A (Ø A)		A	B	A OR B (AÚB)	A AND B (AÙB)

В соответствии с международным стандартом на схемах логические блоки изображаются в следующем виде:

Схема ИЛИ, реализующая операцию логического сложения

Схема И, реализующая операцию логического умножения

 

Схема НЕ, реализующая операцию инверсии

 

Пример 9. Рассмотрим сложное высказывание: «Число 6 делиться на 2, и число 6 делиться на 3». Представить данное высказывание в виде логической формулы.

Обозначим через A простое высказывание «число 6 делиться на 2», а через B «число 6 делиться на 3». Тогда соответствующая логическая формула примет вид: AÙB. Ее значение – ИСТИНА.

 

Пример 10. Вычислить значение логической формулы: не X и Y или X и Z, если логические переменные имеют значения: X = ЛОЖЬ, Y = ИСТИНА, Z = ИСТИНА.

Отметим порядок выполнения операций в логическом выражении:

1) не X – не ЛОЖЬ = ИСТИНА;

2) X и Y – ИСТИНА и ИСТИНА = ИСТИНА;

3) X и Z – ИСТИНА и ЛОЖЬ = ЛОЖЬ;

4) Y или X – ИСТИНА или ЛОЖЬ = ИСТИНА.

Ответ: ИСТИНА.