K – количество символов в сообщении.
2. Содержательный подход (энтропийный). В этом случае количество информации связывается с содержанием полученного человеком сообщения. В теории информации, сообщение , уменьшающее неопределенность наших знаний в два раза, несет 1 бит информации.
Что такое «неопределенность знаний»? лучше всего это объяснить на примерах. Допустим, вы бросаете монету, загадывая, что выпадет: орел или решка? Если всего два варианта возможного результата бросания монеты. Причем ни один из этих вариантов не имеет преимущества перед другим. В таком случае говорят, что они равновероятны.
Формулы Хартли и Шеннона.
Американский инженер Р. Хартли в 1928 г. процесс получения информации рассматривал как выбор одного сообщения из конечного наперёд заданного множества из N равновероятных сообщений, а количество информации I, содержащееся в выбранном сообщении, определял как двоичный логарифм N.
Допустим, нужно угадать одно число из набора чисел от единицы до ста. По формуле Хартли можно вычислить, какое количество информации для этого требуется: I = log2100 6,644. Таким образом, сообщение о верно угаданном числе содержит количество информации, приблизительно равное 6,644 единицы информации. Приведем другие примеры равновероятных сообщений: 1.при бросании монеты: "выпала решка", "выпал орел"; 2."чет-нечет". Но существует множество ситуаций, когда возможные события имеют различные вероятности наступления. Формулу для вычисления количества информации в случае различных вероятностей наступления событий предложил учёный Клод Шеннон в 1948 г.
Легко заметить, что если вероятности p1, ..., pN равны, то каждая из них равна 1 / N, и формула Шеннона превращается в формулу Хартли. Помимо двух рассмотренных подходов к определению количества информации, существуют и другие. Важно помнить, что любые теоретические результаты применимы лишь к определённому кругу случаев, очерченному первоначальными допущениями. |
В качестве минимальной единицы информации Клод Шеннон предложил принять один бит (англ. bit — binary digit — двоичная цифра).
| Бит в теории информации — количество информации, необходимое для различения двух равновероятных сообщений (типа "орел"—"решка", "чет"—"нечет" и т.п.). В вычислительной технике битом называют наименьшую "порцию" памяти компьютера, необходимую для хранения одного из двух знаков "0" и "1", используемых для внутримашинного представления данных и команд. |
Определение количества информации на синтаксическом уровне невозможно без рассмотрения понятия неопределенности состояния (энтропии) системы.
Действительно, получение информации связано с изменением степени неосведомленности получателя о состоянии системы. До получения информации получатель мог иметь предварительные (априорные) сведения о системе a; мера неосведомленности о системе Н(а) и является для него мерой неопределенности состояния системы. После получения некоторого сообщения b получатель приобрел дополнительную информацию Ib(а), уменьшившую его априорную неосведомленность так, что апостериорная (после получения сообщения b) неопределенность состояния системы стала H(а/b).
Тогда количество информации Ib(а) о системе а, полученное в сообщении b, будет определено как
Ib(а)= Н(а)- H(а/b).
Таким образом, количество информации измеряется изменением (уменьшением) неопределенности состояния системы.
Если конечная неопределенность H(а/b) обратится в нуль, то первоначальное неполное знание заменится полным знанием, и количество информации станет равно Ib(а)= Н(а).
Иными словами, энтропия системы Н{а) может рассматриваться как мера недостающей информации.
Энтропия системы H(а), имеющей N возможных состояний, согласно формуле Шеннона, равна
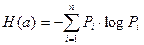
где Pi — вероятность того, что система находится в i-м состоянии. Для случая, когда все состояния системы равновероятны, то есть Pi=1/H энтропия системы
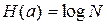
Рассмотрим пример.
По каналу связи передается n-разрядное сообщение, использующее т различных символов, так что количество всевозможных кодовых комбинаций будет N = тп.
При равновероятном появлении любой кодовой комбинации количество информации в правильном сообщении — формула Хартли:
I = logN = n*logm.
Если в качестве основания логарифма принять m, то I = п.
В данном случае количество информации (при условии полного априорного незнания получателем содержания сообщения) будет равно объему данных I = Vд.
Для неравновероятных состояний системы всегда I<VД, VД=n.
Наиболее часто используются двоичные и десятичные логарифмы. Единицами измерения в этих случаях будут, соответственно, бит и дит.
Степень информативности сообщения Y определяется отношением количества информации к объему данных, то есть Y = I/VД, причем 0 < Y < 1 (Y характеризует лаконичность сообщения).
С увеличением Y уменьшается объемы работ по преобразованию информации (данных) в системе. Поэтому для повышения информативности сообщений разрабатываются специальные методы оптимального кодирования информации.
Дата добавления: 2015-10-19; просмотров: 1576;

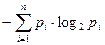 , где pi — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.
, где pi — вероятность того, что именно i-е сообщение выделено в наборе из N сообщений.