Очевидно, что значение среднего квадратического, полученное по формуле (7), во всех этих примерах весьма приближенно и указывает лишь на порядок этой величины.
Для определения средней арифметической часто употребляют метод условной средней. Этот метод особенно удобен в том случае, когда варианты выражаются сложными числами и вычислительные операции над ними затруднительны (минуты и секунды). При использовании метода условной средней один из вариантов условно принимают за среднюю величину. В дальнейшем работа сводится к определению некоторой поправки, представляющей собой разность между истинной и условной средней. Эта поправка есть взвешенная сумма отклонений вариантов от условно средней, деленная на объем совокупности:
b = 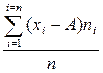
где b—поправка для учета отклонения истинной средней от условной;
хi— варианты;
А—условная средняя;
ni — частоты;
n—объем совокупности.
Искомая средняя арифметическая есть сумма условной средней и найденной поправки:
X = A + b =A + 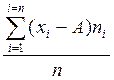 (9)
(9)
Рассчитать на примере 2
| xi | ni | xi - A | (xi – A) ni |
| -7 | -28 | ||
| -3 | -18 | ||
| n=34 |
А=81; b=8/34=0,24
 =A+b=81+0,24=81,24 » 81
=A+b=81+0,24=81,24 » 81
Сами на примерах 3 и 4.
Дата добавления: 2015-10-19; просмотров: 829;
