Состав Р-кадра

Вернемся к вычитанию одного кадра из другого. Давайте перед этим вычитанием мы выполним компенсацию движения, т. е. получим информацию о движущихся участках. При этом сами участки исключим из вычитания, посчитав, что на месте этих участков при вычитании будут нули. Собственно, зачем нам их вычитать, ведь всю информацию об этих участках мы уже имеем — зачем дублировать информацию? Чем меньше информации, тем нам лучше — в этом и суть компрессии. Таким образом, количество нулей в остаточном кадре увеличится — добавятся нули там, где мы выполнили компенсацию движения.

Таким образом, после всех ранее описанных манипуляций, мы будем иметь следующую информацию, которую для наглядности покажем графически (рис. 3.12).

Рис. 3.12. Состав Р-кадра

Ключевой кадр передается без изменений (или подвергается внутрикадровой компрессии), а вот остаточный кадр и информацию о движении подвергают дальнейшей компрессии.

Рассмотрим, как компрессируется остаточный кадр. После получения остаточного кадра, он разбивается на прямоугольные участки (8x8 точек, 16x16 точек и т. п.). К каждому такому участку применяется дискретно-косинусное преобразование или иначе Discrete Cosine Transform сокращенно — DCT.

Давайте рассмотрим некий произвольный участок остаточного кадра размером 8x8 точек (рис. 3.13). Каждая точка этого участка в цифровом виде представляет собой число. В общем случае, точки разных яркостей и цветов могут иметь любую комбинацию, поэтому и числа тоже могут иметь любую комбинацию, поскольку мы рассматриваем произвольное придуманное изображение.

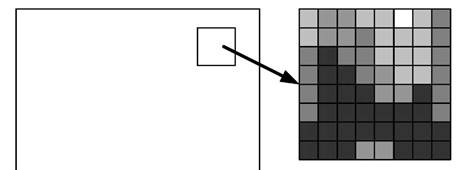
Рис. 3.13. Блок изображения 8x8 точек

Так вот чем хорошо DCT — оно описывает любую произвольную комбинацию чисел при помощи упорядоченной комбинации чисел.

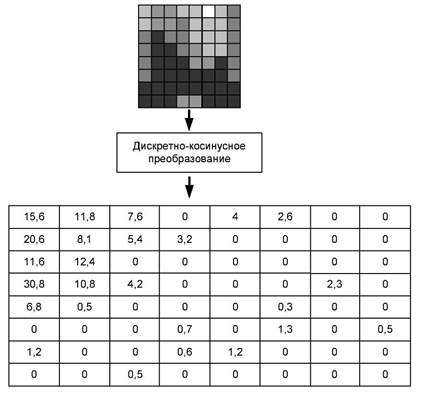
Рис. 3.14. Получение матрицы коэффициентов DCT

Итак, из иллюстрации мы видим (рис. 3.14), что в результате DCT получилась таблица 8x8 ячеек, при этом числа, имеющие наибольшее значение, размещены в левом верхнем углу таблицы. Каких бы яркостей и цветов не были точки на исходном изображении 8x8, расположение чисел после применения DCT всегда будет примерно таким, как показано. Таким образом, числа, имеющие наибольшее значение, всегда будут иметь тенденцию к "скучива- нию" в левом верхнем углу. Соответственно, к правому нижнему углу будут группироваться нулевые значения.

Теперь произведем квантизацию данных в таблице. В нашем примере произведено квантование с шагом 3. То есть 3 = 1, 6 = 2, 9 = 3 и т. д. В реальных алгоритмах уровни квантования могут быть любыми.

Теперь считаем данные из таблицы (как показано на рис. 3.15) и запишем последовательности повторяющихся чисел парами (N, M), где N — количество повторений, а M — повторяющееся число. Такой способ записи называется групповым кодированием (run-length encoding — RLE).

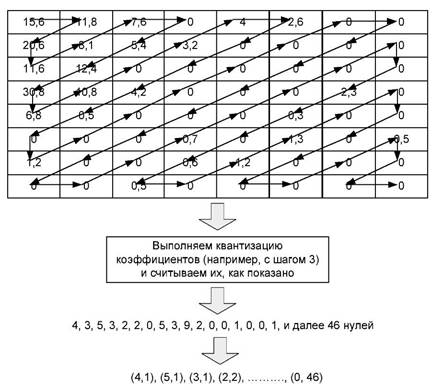
Рис. 3.15. Считывание коэффициентов DCT и их сокращенная запись

Получившаяся запись через пары (N, M) будет гораздо короче, чем запись исходного изображения в цифровом виде — т. е. мы продвинулись еще дальше в компрессии нашего изображения и имеем компрессированный остаточный кадр (residual frame).

В реальных алгоритмах компрессирование остаточного кадра выполняется сложнее, в частности, выбираются различные размеры ячеек, к которым применяется DCT, используются разные уровни квантования, разные "маршруты" считывания результатов DCT и т. п.

После совершения всех приведенных манипуляций, выполняется дополнительное сжатие, которое называется энтропийным кодированием. Суть энтропийного кодирования сводится к тому, что в последовательности чисел, которая подвергается компрессии, находятся закономерности вероятностного характера, которые и используются для кодирования.

Упрощенно, идея такого кодирования достаточно понятна: предположим, что у нас есть последовательность групп чисел: 111, 110, 111, 112, 111, 110, 080, 011, 111, 126, 135 и т. д. Пусть в этой последовательности 111 встречается 400 раз, 110 — 200 раз и остальные варианты — по 1 разу. Обозначим группу 111 числом 1, как самую часто встречающуюся, 110 числом — 2 и т. п. И будем группы "зашифровывать" при передаче этими числами. Первые 10 "шифров" будут однозначными числами (0...9), следующие — двузначными и т. п.

Поскольку в реальности количество разных вариантов групп может доходить до сотен, то ясно, что такое кодирование приведет к снижению потока информации при передаче. Действительно — наиболее часто будут встречаться "шифры" самых часто встречающихся групп, и эти шифры как раз и будут самыми короткими (т. е. содержать меньшее количество чисел). Подобное встречается в обычном человеческом языке — самые употребительные слова, как правило, являются самыми короткими (я, небо, река и т. п.

Энтропийному кодированию может быть подвергнута любая цифровая информация — как компенсация движения, так и компрессированный остаточный кадр. Существует несколько алгоритмов энтропийного кодирования: кодирование Хаффмана, арифметическое кодирование и т. п.

Готовая компрессированная последовательность форматируется в виде элементарного потока MPEG.

Для примера, на рис. 3.16 приведена условная формула, по которой происходит сборка Р-кадра в декодере.

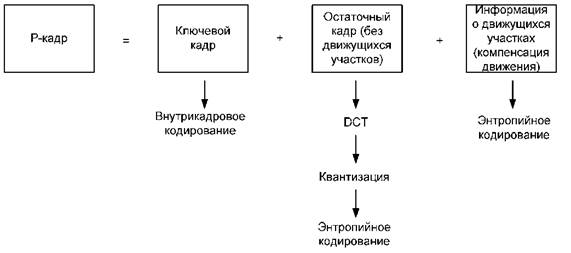
Рис. 3.16. Состав Р-кадра с указанием примененных алгоритмов.).

Теперь рассмотрим, что происходит в декодере. В декодер сначала приходит ключевой кадр, который декомпрессируется (если к нему применялась внут- рикадровая компрессия) и сохраняется в памяти декодера. Этот кадр будет необходим в дальнейшем, поскольку он используется для "предсказания" кадров GOP, которые идут за ним. После того как прошла вся GOP, ключевой кадр удаляется из памяти, уступая свое место ключевому кадру следующей GOP.

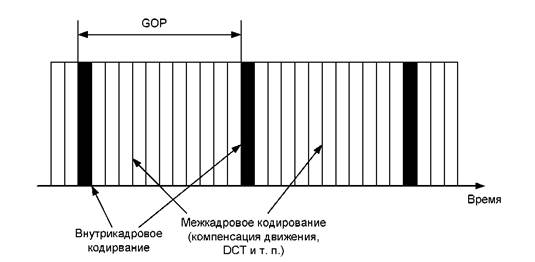
Рис. 3.17. Межкадровое и внутрикадровое кодирование

После ключевого кадра начинают один за другим поступать P-кадры, которые представляют собой информацию об отличиях этих кадров от ключевого кадра (рис. 3.17). Информация эта состоит из двух частей, как мы видели: из векторов движения и участков, которые они описывают, а также остаточного кадра, обработанного DCT. И то и другое подвергнуто энтропийному кодированию.

Получив Р-кадр, декодер производит энтропийное декодирование всей информации, затем применяет обратное дискретно-косинусное преобразование, получая остаточный кадр. Этот остаточный кадр складывается с ключевым кадром. После этого выполняется компенсация движения — т. е. из ключевого кадра "выдергиваются" участки, которые переместились и складываются с полученным суммарным кадром в местах, определяемых векторами движения. В результате получается готовый кадр (рис. 3.18).

Последовательность готовых кадров передается на устройство, демонстрирующее ее зрителю (например, устройство интерфейса HDMI).

Опорный кадр Опорный кадр + компенсация

движения

Рис. 3.18. Порядок декомпрессирования изображения