Гироскопы
Кинетическая энергия вращающегося тела.
Момент инерции материальной точки и тела.
Момент инерции сплошного диска.
Момент силы.
Момент импульса.
6 Уравнение вращательного движения твёрдого тела.
Гироскопы
1. Центр масс твёрдого тела, центр инерции, движение центра масс.
Разбив тело на элементарные массы 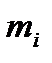 его можно представить как сумму материальных точек;
его можно представить как сумму материальных точек; 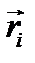 – радиус вектор, определяемый положением этой элементарной массы.
– радиус вектор, определяемый положением этой элементарной массы.
Центр масс твёрдого тела – точка с радиус-вектором 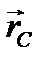
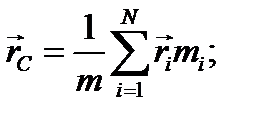
Можно показать, что для системы материальных точек выполняется уравнение:
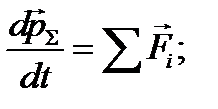
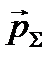 – суммарный импульс;
– суммарный импульс; 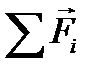 сумма всех сил. Продифференцируем
сумма всех сил. Продифференцируем 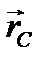 поt; найдём скорость центра масс:
поt; найдём скорость центра масс:
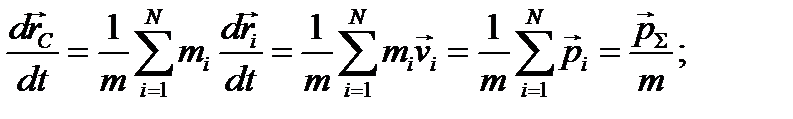
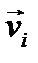 и
и 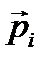 - скорость и импульс частицы.
- скорость и импульс частицы.
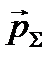 - импульс системы.
- импульс системы.
Полный импульс системы можно представить в виде произведения массы на системы на скорость движения центра масс:
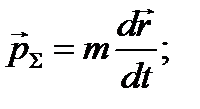 тогда
тогда 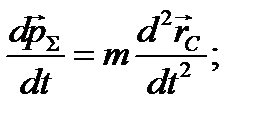
По третьему закону Ньютона:
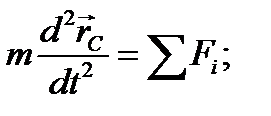
Теорема о движении центра масс твёрдого тела
Центр масс твёрдого тела движется так, как двигалась бы материальная точка с массой, равной массе тела, под действием всех приложенных сил (центр масс совпадает с центром тяжести тела в однородном поле сил тяжести).
Уравнение даёт возможность установить движение центра масс твёрдого тела, если известна масса тела и действующие на него силы.
2 Кинетическая энергия вращающегося тела. Момент инерции материальной точки твёрдого тела.
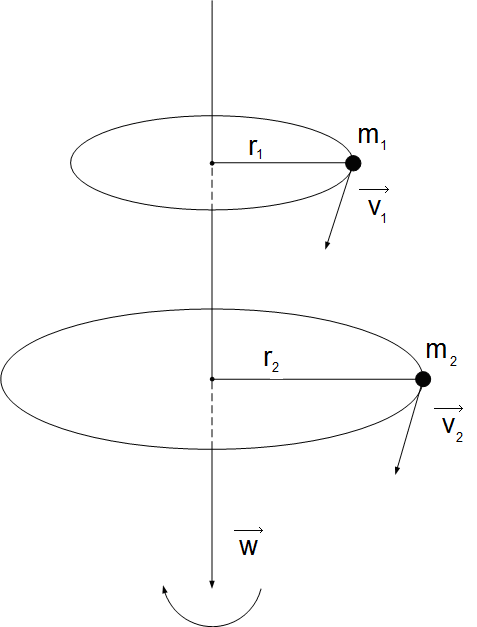
Мысленно разобьём тело, вращающееся вокруг неподвижной оси с угловой скоростью 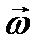 на элементарнее массы
на элементарнее массы 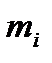 ;
; 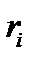 – расстояние от массы до оси;
– расстояние от массы до оси; 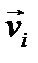 - линейная скорость i-той массы.
- линейная скорость i-той массы.
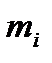 ;
; 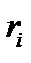 ,
, 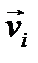 , модуль.
, модуль.
Тогда кинетическая энергияi-той точки:
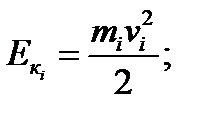
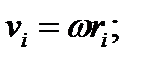
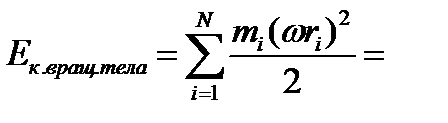
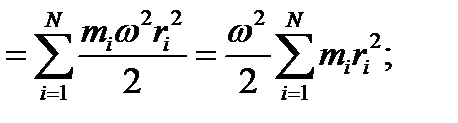
Моментом инерции i-той массы тела относительно оси вращения называется произведение массы материальной точки на квадрат её расстояния от оси вращения.
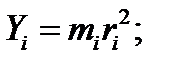
Момент инерции твёрдого тела относительно оси вращения складывается из суммы моментов инерции всех материальных точек, составляющих тело относительно этой оси.
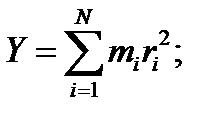
Тогда:
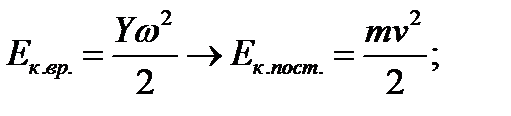
Дата добавления: 2015-10-13; просмотров: 572;
