Теплообмене
| № п/п | Наименование величины | Показатель степени | Размерности | ||||
| кг | м | с | °К | Дж | |||
| l | il | - | |||||
| u | iu | -2 | -1 | ||||
| m | im | -1 | -1 | ||||
| r | ir | -3 | |||||
| l | il | -1 | -1 | -1 | |||
| С | ic | -1 | -1 | ||||
| a | -1 | -2 | -1 | -1 |
Исключаем размерности:
1 — (кг) iu + im + ir - ic = 0
2 — (м) il - 2iu - im - 3ir - il+ 2 = 0
3 — (c) - il -im - il+ 1 = 0
4 — (°К) - il - ic + 1 = 0
5 — (Дж) il + ic - 1 = 0.
Как видно из последних двух уравнений, полученных исключением размерности, они тождественны, т. к. определяются из теплоемкости воды. Таким образом, имеем 4 независимых уравнения связи при шести независимых переменных. Следовательно, в исходной системе уравнений только два неизвестных показателя подлежат экспериментальному определению, а остальные определяются по полученной системе уравнений в зависимости от этих двух основных. Например, в опыте определены показатели и они соответственно равны: iu= n; ic = m (n, m — число); тогда, используя систему уравнений, получим:
из 4 — il= 1 - ic= 1 - m
из 3 — im = - iu - il + 1 = -n + 1 + m - 1 = m - n
из 1 — ir = ic - iu - im = m - n - m + n = 0
из 2 — il = 2iu + im + il + 3ir - 2 = 2n + m - n +1 - m - 2 = n - 1.
Подставив полученные значения показателей в (4.48), получим
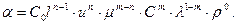 (4.49)
(4.49)
Преобразуем полученные уравнения, сгруппировав величины с одинаковыми показателями
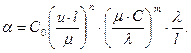 (4.50)
(4.50)
или
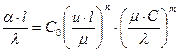 , (4.51)
, (4.51)
где ul/μ = ωl/ν = Re — критерий Рейнольдса — критерий гидродина-мического подобия;
μС/λ = ν/a = Pr — критерий Прандтля — критерий теплофизического подобия;
αl/λ = Nu — критерий Нуссельта — критерий теплового подобия.
Таким образом, на основании теории размерностей получено уравнение связи безразмерных параметров, характеризующих теплообмен в условиях вынужденной конвекции и число независимых переменных снижено с 6 до 2, что обеспечивает возможность их экспериментального определения, и тогда N=An=100.
Правильность использования теории размерностей подтверждается π-теоремой, исходя из чего физическое уравнение, содержащее n³2 размерных величин, из которых m³1 имеют независимые размерности, после приведения их к безразмерному виду должно содержать n безразмерных параметров n = n – m. В нашем случае n = n – m = 6 – 4 = 2. Численные значения постоянных, входящих в уравнение (4.51) С0, n, m, определяются экспериментально и в зависимости от вида теплообмена приводятся в справочной литературе, некоторые даны в табл. 4.3.
Дата добавления: 2015-10-13; просмотров: 702;
