Теплопередача при конвективном теплообмене

19.1 Теплопередача через плоскую стенку

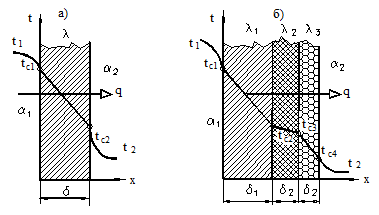Если плоская стенка толщиной d и теплопроводностью l разделяет две жидкостные или газовые среды, имеющие разные температуры, то при этом возникает тепловой поток от горячей среды к холодной (рисунок 19.1,а).

Плотность теплового потока, передаваемого от горячей среды к стенке, составляет

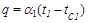, (19.1)

где - коэффициент теплоотдачи от горячей среды к стенке, - температура горячей среды, 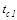- температура стенки.

Если стенка не ограничена по высоте и ширине, то в условиях стационарного режима через любую изотермическую поверхность в стенке будет передаваться один и тот же тепловой поток

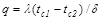, (19.2)

где 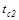- температура стенки со стороны холодной cреды.

При теплоотдаче от стенки к холодной среде плотность теплового потока равна

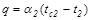, (19.3)

где 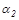- коэффициент теплоотдачи от стенки к холодной среде, 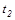- температура холодной cреды.

При решении уравнений (19.1-19.3) относительно разности температур, получается следующее:

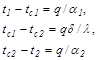(19.4)

Сложение левых и правых частей уравнений (19.4) позволяет определить зависимость плотности теплового потока от параметров теплопередачи:

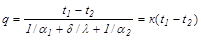, (19.5)

где коэффициент теплопередачи равен

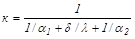(19.6)

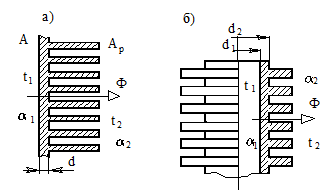
В случае теплопередачи через n-слойную плоскую стенку (рисунок 19.1,б) коэффициент теплопередачи равен

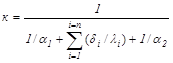, (19.7)

где 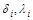- толщина и теплопроводность i-го слоя.

Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением:

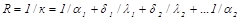(19.8)

Температуры на наружных поверхностях стенки определяются по формулам

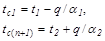(19.9)

Для определения температуры на границе между i-м и (i+1)-м слоями используется формула

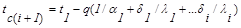(19.10)

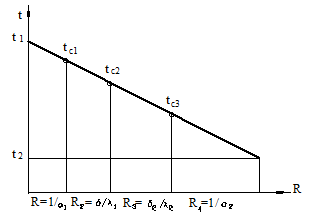
Температуры на стыках между слоями могут быть определены графическим методом (рисунок 19.2). Для этого на горизонтальной оси последовательно откладываются значения частных термических сопротивлений

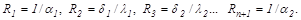, ( 19.11)

а на температурной оси откладываются значения температур горячей и холодной сред. Точки 1 и 2 соединяются прямой линией. Пересечение этой линии с восстановленными перпендикулярами с оси R дает значения искомых температур.

19.2 Теплопередача через цилиндрическую стенку

Особенность теплопередачи через цилиндрическую стенку заключается в том, что поверхности теплообмена снаружи и внутри трубы различны. Исходя из схемы передачи теплоты, представленной на рисунке 19.3,а, можно записать для теплового потока, передаваемого через цилиндрическую стенку, следующие формулы:

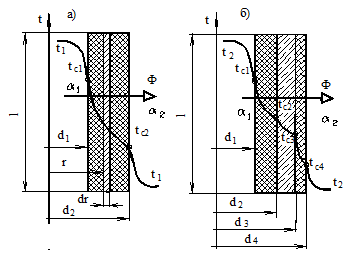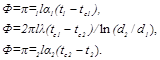(19.12)

После решения этих уравнений относительно разности температур и последующего сложения левых и правых частей получается следующее выражение:

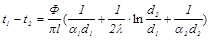(19.13)

Из (19.13) следует

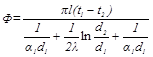(19.14)

Если тепловой поток отнести к 1 метру трубы, то формула (19.14) примет следующий вид

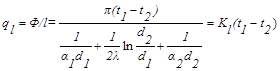, 19.15)

где 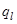- линейная плотность теплового потока, равная тепловому потоку, передаваемому через стенку цилиндра длиной 1 м; к_l – линейный коэффициент теплопередачи, равный

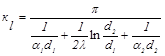(19.16)

При теплопередаче через многослойную цилиндрическую стенку линейная плотность теплового потока определяется по формуле

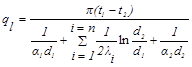, (19.17)

где i - порядковый номер слоя, n - число слоев

19.3 Теплоизоляция труб

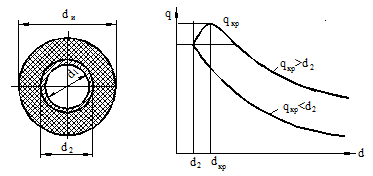
Для снижения тепловых потерь трубы покрывают изоляционными материалами, имеющими низкую теплопроводность: асбестом, минеральной ватой, пенопластом и др.

Если при изоляции плоских поверхностей общее термическое сопротивление всегда возрастает, а тепловой поток уменьшается, то изоляция цилиндрических поверхностей иногда приводит к отрицательному эффекту и увеличению тепловых потерь.

Формула для определения линейной плотности теплового потока при теплопередаче через изолированную однослойную стенку имеет вид:

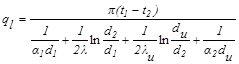(19.18)

Как видно из формулы (19.18), с увеличением диаметра 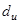и толщины изоляции линейная плотность потока зависит от двух последних слагаемых знаменателя, причем слагаемое, учитывающее передачу теплоты теплопроводностью, возрастает, а слагаемое, учитывающее теплоотдачу с наружной поверхности, уменьшается. Суммарное их влияние может привести как к росту, так и к уменьшению передаваемой теплоты. Для выявления экстремума функции следует взять первую производную от суммы этих слагаемых и приравнять её нулю:

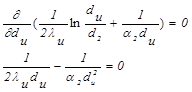
Из последнего выражения получается формула для критического диаметра изоляции, соответствующего экстремальному значению:

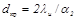(19.19)

Формула (19.19) говорит о том, что критический диаметр изоляции зависит только от соотношения теплопроводности изоляционного материала и коэффициента наружной теплоотдачи.

На рисунке 19.4 показаны графики тепловых потерь в зависимости от диаметра изоляции для двух возможных вариантов. В том случае, когда критический диаметр изоляции больше наружного диаметра трубы (верхняя кривая ) применение изоляции нецелесообразно и вредно до значений 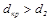. Если критический диаметр изоляции меньше наружного диаметра трубы (нижняя кривая), то применение изоляции возможно и полезно.

19.4 Теплопередача через ребристую стенку

Оребренные поверхности применяют в двигателях внутреннего сгорания с воздушным охлаждением цилиндров, в компрессорах и различных теплообменниках для выравнивания термических сопротивлений теплоотдачи с обеих сторон стенки в тех случаях, когда они значительно различаются по величине. Оребрение производится всегда со стороны меньшего коэффициента теплоотдачи.

Оребрённая плоская стенка показана на рисунке 19.5,а .

Пусть параметры гладкой стороны - 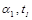, оребренной стороны - 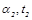, площадь гладкой поверхности - A, площадь ребристой поверхности - 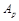, теплопроводность стенки - l и толщина стенки без учета ребер - d

В этих условиях процесс теплопередачи описывается уравнениями:

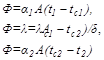(19.20)

При решении этой системы уравнений, по ранее применяемой в п.19.1 схеме, получается:

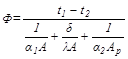(19.21)

Если тепловой поток отнести к площади гладкой поверхности, то получается формула для плотности теплового потока

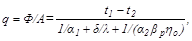(19.22)

где 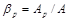- коэффициент оребрения

Для круглой трубы, имеющей наружное оребрение (рисунок 19.5,б), тепловой поток определяется по формуле

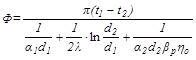(19.23)

Из-за изменения температуры по высоте рёбер теплоотдача у вершины меньше чем у основания, поэтому для корректировки коэффициента оребрения вводится коэффициент эффективности ребристой поверхности h_о , который всегда меньше единицы и определяется по формуле :

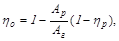(19.24)

где η_р– коэффициент эффективности ребра, определяемый по специальной методике.

Более подробно об этом дано в следующем параграфе 19.5.

19.5 Теплопроводность в ребре постоянного

поперечного сечения

На рисунке 19.6,а показано ребро постоянного сечения на плоской поверхности. Геометрические размеры ребра следующие: высота – L, ширина – b, толщина – 2h . Предполагается, что температура ребра Т изменяется только вдоль оси z , теплота передаётся в окружающую среду только с верхней и нижней поверхностей, а коэффициент теплоотдачи с наружных поверхностей ребра α – величина постоянная.

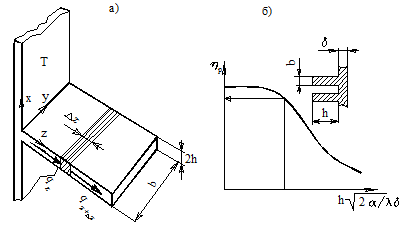Для выделенного элементарного объёма ребра на основании теплового баланса можно записать

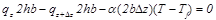(19.25)

При делении уравнения (19.25) на 2hbΔz и определении предела при Δя→0 , получается

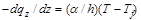(19.26)

С учётом уравнения Фурье выражение (19.26) имеет вид:

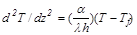(19.27)

Это уравнение определяет изменение температуры по высоте ребра в условиях передачи теплоты теплопроводностью вдоль ребра с одновременной теплоотдачей с поверхностей ребра в окружающую среду. Решение уравнения (19.27) обычно приводится в графическом виде с безразмерными координатами η_р - 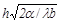, как это показано на рисуне19.6,б. Аналогичные графики существуют для рёбер иной конфигурации на плоских и цилиндрических поверхностях.

Дата добавления: 2015-11-10; просмотров: 2045;