Приток к скважине в пласте с прямолинейным контуром питания. Пусть в полосообразном пласте пробурена одна скважина с центром в точке О1на расстоянии а от прямолинейного контура (ось у ) бесконечного протяжения

Пусть в полосообразном пласте пробурена одна скважина с центром в точке О₁на расстоянии а от прямолинейного контура (ось у ) бесконечного протяжения, на котором поддерживается постоянный потенциал j_к . На скважине радиуса r_cподдерживается постоянный потенциал j_с. Найдём дебит скважины Gи распределение функции j.

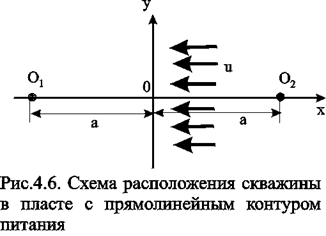
Так как контур питания пласта 0уявляется эквипотенциальной линией, то все линии тока, сходящиеся в центре скважины О₁, должны быть перпендикулярны к прямой 0у (рис.4.6). Для определения поля течения добьёмся выполнения граничных условий на контуре введением фиктивного источника О₂ с дебитом, равным дебиту стока О₁, путём зеркального отображения данного стока относительно прямой 0у.Т.о. используем ранее упомянутый метод отображения и задачу о потоке в пласте с прямолинейным контуром питания и с одиночной эксплуатационной скважиной сведём к ранее рассмотренной в разделе 4.1.1. задаче о совместном действии источника и стока равной производительности. Отличие данных задач только в постановке граничных условий: в задаче раздела 4.1.1. источник питания - нагнетательная скважина, а в данном случае - прямолинейный контур, а источник О₂фиктивный.

Т.о. используем для определения дебита выражение (4.10), но со следующей заменой граничных условий:

j=j_к при r₁=r₂ ,т.е. при r₁/r₂=1;

j=j_с при r₁=r_с , r₂»2а, т.е. при r₁/r₂» r_с /2а;

Подставляя последовательно соответствующие граничные значения j, r₁и r₂ в равенство (4.10) получим два уравнения, определяющих потенциалы на контуре и забое. Из этих уравнений легко находится массовый дебит одиночной скважины в пласте с прямолинейным контуром

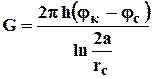. 4.18

Если бы в пласте была нагнетательная скважина, то в формуле (4.18) достаточно только изменить знак правой части.