СХЕМНАЯ РЕАЛИЗАЦИЯ ЭЛЕМЕНТАРНЫХ ЛОГИЧЕСКИХ ОПЕРАЦИЙ. ТИПОВЫЕ ЛОГИЧЕСКИЕ УЗЛЫ
Мы уже знаем, что любую достаточно сложную логическую функцию можно реализовать, имея относительно простой набор базовых логических операций. Первоначально этот тезис был технически реализован «один к одному»: были разработаны и выпускались микросхемы, соответствующие основным логическим действиям. Потребитель, комбинируя имеющиеся в его распоряжении элементы, мог получить схему с реализацией необходимой логики. Довольно быстро стало ясно, что подобное «строительство здания из отдельных кирпичиков» не может удовлетворить практические потребности. Промышленность увеличила степень интеграции МС и начала выпускать более сложные типовые узлы: триггеры, регистры, счетчики, дешифраторы, сумматоры и т.д. (продолжая аналогию со строительством, этот шаг, видимо, следует уподобить панельному способу домостроения). Новые микросхемы давали возможность реализовывать еще более сложные электронные логические устройства, но человеку свойственно не останавливаться на достигнутом: рост возможностей порождает новые потребности. Последовал переход к большим интегральным схемам (БИС), представлявшим из себя функционально законченные узлы, а не отдельные компоненты для их создания (как тут не вспомнить блочный метод постройки здания из готовых комнат). Наконец, дальнейшая эволюция технологий производства ИМС привела к настолько высокой степени интеграции, что в одной БИС содержалось функционально законченное изделие: часы, калькулятор, небольшая специализированная ЭВМ...
Если посмотреть на внутреннее устройство типичного современного компьютера, то там присутствуют ИМС очень высокого уровня интеграции: микропроцессор, модули ОЗУ, контроллеры внешних устройств и др. Фактически каждая микросхема или небольшая группа микросхем образуют функционально законченный блок. Уровень сложности блока таков, что разобраться в его внутреннем устройстве для неспециалиста не только нецелесообразно, а просто невозможно. К счастью, для понимания внутренних принципов работы современной ЭВМ достаточно рассмотреть несколько типовых узлов, а изучение поведения БИС заменить изучением функциональной схемы компьютера.
Обработка информации в ЭВМ происходит, как уже не раз отмечалось выше, путем последовательного выполнения элементарных операций. Эти операции менее многочисленны, нежели набор команд ЭВМ (которые реализуются через цепочки этих операций). К элементарным операциям относятся: установка - запись в операционный элемент (например, регистр) двоичного кода; прием - передача (перезапись) кода из одного элемента в другой; сдвиг - изменение положения кода относительно исходного; преобразование - перекодирование; сложение - арифметическое сложение целых двоичных чисел - и некоторые другие. Для выполнения каждой из этих операций сконструированы электронные узлы. являющиеся основными узлами цифровых вычислительных машин - регистры, счетчики, сумматоры, преобразователи кодов и т.д.
В основе каждой из элементарных операций лежит некоторая последовательность логических действий, описанных в предыдущем параграфе. Проанализируем, например, операцию сложения двух чисел: 3+6.Имеем:
+ 110
На каждом элементарнейшем шаге этой деятельности двум двоичным цифрам сопоставляется двоичное число (одно- или двузначное) по правилам: (0,0) => О, (0,1) => 1, (1.0) => 1, (1,1) => 10. Таким образом, сложение цифр можно описать логической бинарной функцией. Если дополнить это логическим правилом переноса единицы в старший разряд (оно будет сформулировано ниже при описании работы сумматора), то сложение полностью сведется к цепочке логических операций.
Для дальнейшего рассмотрения необходимо знать условные обозначения базовых логических элементов. Они приведены на рис. 4.21. Соответствующие таблицы истинности приведены в предыдущем пункте.
Отметим, что на практике логические элементы могут иметь не один или два, а значительно большее число входов.
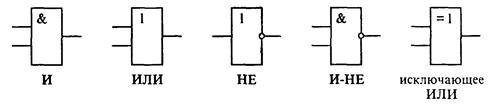
Рис. 4.21. Условные обозначения основных логических элементов
Итак, примем к сведению, что простейшие логические элементы, изображенные на рис. 4.21, можно реализовать аппаратно. Это означает, что можно создать электронные устройства на транзисторах, резисторах и т.п., каждое из которых имеет один или два входа для подачи управляющих напряжений и один выход, напряжение на котором определяется соответствующей таблицей истинности. На практике логическому «да» («истина», или цифра 1 в таблицах истинности) соответствует наличие напряжения, логическому «нет» («ложь», или цифра 0) - его отсутствие.
Вопрос, на который мы должны ответить, таков: как с помощью таких элементарных схем реализовать сложные цифровые устройства, необходимые для работы ЭВМ? При этом, учитывая существование прямых соответствий между логическими и электронными схемами, вполне достаточно достичь понимания на уровне логических схем.
В качестве характерных устройств выберем два наиболее важных и интересных -триггер (рис. 4.22) и сумматор. Первый - основа устройств оперативного хранения информации, второй служит для сложения чисел.
Перейдем к описанию работы триггера.Соответствующая его работе таблицаистинности (табл. 4.7) приведена ниже.
Как видно из рис. 4.22, простейший вариант триггера собирается из четырех логических элементов И-НЕ, причем два из них играют вспомогательную роль. Триггер имеет два входа, обозначенные на схеме R и S, а также два выхода, помеченные буквой Q - прямой и инверсный (черта над Q у инверсного выхода означает отрицание). Триггер устроен таким образом, что на прямом и инверсном выходах сигналы всегда противоположны.
Как же работает триггер? Пусть на входе R установлена 1, а на S - 0. Логические элементы D1 и D2 инвертируют эти сигналы, т.е. меняют их значения на противоположные. В результате на вход элемента D3 поступает 1, а на D4 - 0. Поскольку на одном из входов D4 есть 0. независимо от состояния другого входа на его выходе (он же является инверсным выходом триггера!) обязательно установится 1. Эта единица передается на вход элемента D3 и в сочетании с 1 на другом входе порождает на выходе D3 логический 0. Итак, при R=1 и S=0 на прямом выходе триггера устанавливается 0, а на инверсном - 1.
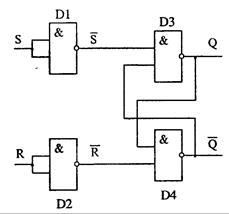
Рис. 4.22. Логическая схема триггера
Таблица 4.7
Таблица истинности RS-тригтера
| S | R | 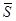
| 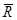
| Q | 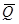
| Примечания |
| X (1 | X 1) | Хранение Запрещено |
Обозначение состояния триггера по договоренности связывается с прямым выходом. Тогда при описанной выше комбинации входных сигналов результирующее состояние можно условно назвать нулевым: говорят, что триггер «устанавливается в 0» или «сбрасывается». Сброс по-английски называется «Reset», отсюда вход, появление сигнала на котором приводит к сбросу триггера, обычно обозначают буквой R.
Проведите аналогичные рассуждения для «симметричного» случая R =0 и S = 1. Вы увидите, что на прямом выходе получится логическая 1, а на инверсном - 0. Триггер перейдет в единичное состояние - «установится» (установка по-английски - «Set»).
Теперь рассмотрим наиболее распространенную и интересную ситуацию R = 0 и S = 0 - входных сигналов нет. Тогда на входы элементов D3 и D4. связанные с R и S будет подана и их выходной сигнал будет зависеть от сигналов на противопо-ложных входах. Нетрудно убедится, что такое состояние будет устойчивым. Пусть, например, на прямом выходе 1. Тогда наличие единиц на обоих входах элемента D4 «подтверждает» нулевой сигнал на его выходе. В свою очередь, наличие 0 на инверсном выходе передается на D3 и поддерживает его выходное единичное состояние. Аналогично доказывается устойчивость картины и для противоположного состояния триггера, когда Q = 0.
Таким образом, при отсутствии входных сигналов триггер сохраняет свое «предыдущее» состояние. Иными словами, если на вход R подать 1, а затем убрать, триггер установится в нулевое состояние и будет его сохранять, пока не поступит сигнал на другой вход S. В последнем случае он перебросится в единичное состояние и после прекращения действия входного сигнала будет сохранять на прямом выходе 1. Мы видим, что триггер обладает замечательным свойством: после снятия входных сигналов он сохраняет свое состояние, а значит может служить устройством для хранения одного бита информации.
В заключение проанализируем последнюю комбинацию входных сигналов: R = 1 и S = 1. Нетрудно убедиться (проделайте необходимые рассуждения самостоятельно), что в этом случае на обоих выходах триггера установится I! Такое состояние помимо своей логической абсурдности еще и является неустойчивым: после снятия входных сигналов триггер случайным образом перейдет в одно из своих устойчивых состояний. Вследствие этого, комбинация R = 1 и S = 1 никогда не используется на практике и является запрещенной.
Мы рассмотрели простейший RS-триггер. Существуют и другие разновидности этого интересного и полезного устройства. Все они различаются не столько принципом работы, сколько входной логикой, усложняющей «поведение» триггера.
Триггеры очень широко применяются в вычислительной технике. На их основе изготовляются всевозможные регистры для хранения и некоторых видов обработки (например, сдвига) двоичной информации, счетчики импульсов и даже интегральные микросхемы статического ОЗУ, не требующие для сохранения информации специальных процессов регенерации. Множество триггеров входят в состав любого микропроцессора.
В качестве второго примера применения логических элементов в вычислительной технике рассмотрим устройство, называемое сумматором. Его назначение состоит в нахождении суммы двух двоичных чисел. Этот узел интересен для нас тем, что он лежит в основе арифметического устройства ЭВМ и иллюстрирует некоторые принципы выполнения вычислительных операций в компьютере.
Для простоты начнем с изучения логической структуры простейшего возможного устройства, являющегося звеном сумматора. Это устройство - полусумматор - реализует сложение двух одноразрядных двоичных, чисел, которые обозначим А и В. В результате получается, вообще говоря, двухразрядное двоичное число. Его младшую цифру обозначим S, а старшую, которая при сложении многоразрядных чисел будет перенесена в старший разряд, через Со (от английских слов «Carry out»- «выходной перенос»). Для лучшего понимания происходящего вспомните правило типа «ноль пишем, один в уме».
Обе цифры можно получить по следующим логическим формулам:
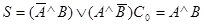
(черта над символом обозначает операцию NOT, знак ^ - конъюнкцию, знак v -дизъюнкцию). Это легко проверить перебором всех четырех возможных случаев сочетания значений А и В, пользуясь табл. 4.5 и табл. 4.8.
Таблица 4.8
Таблица истинности для полусумматора
| А | В | S | Со |
Мысленно объединим в табл. 4.8 столбцы А, В и Со. Полученная таблица напоминает базовый логический элемент И. Аналогично, сравнив первые три столбца А.В и S с имеющимися в предыдущем разделе таблицами истинности для распространенных логических элементов, обнаружим подходящий для наших целей элемент «исключающее ИЛИ». Таким образом, для реализации полусумматора достаточно соединить параллельно входы двух логических элементов (рис. 4.23).
Ниже приведены два варианта логической схемы полусумматора: с использованием лишь базовых логических элементов и с использованием логического элемента «исключающее ИЛИ». Видно, что вторая схема существенно проще.
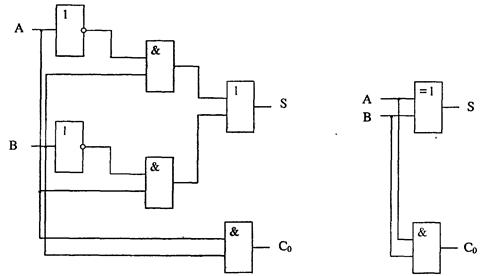
Рис. 4.23. Логическая схема полусумматора (два варианта)
Полный одноразрядный сумматор «умеет» при сложении двух цифр учитывать возможное наличие единицы, переносимой из старшего разряда (той, которая при обычном сложении столбиком остается «в уме»). Обозначим этот «бит переноса» через Ci (от английского «Carry in» - «входной перенос»).
Таблица 4.9
Таблица истинности для полусумматора
| Входы | Выходы | ||||
| А | В | Ci | S | Со | |
При построении схемы сумматор удобно представить в виде двух полусумматоров, из которых первый суммирует разряды А и В, а второй к полученному результату прибавляет бит переноса Ci.
Заметим, что для суммирования младших разрядов чисел полусумматора уже достаточно, так как в этом случае отсутствует сигнал входного переноса.
Соединив два полусумматора как показано на рис. 4.24, получим полный сумматор, способный осуществить сложение двух двоичных разрядов с учетом возможности переноса.
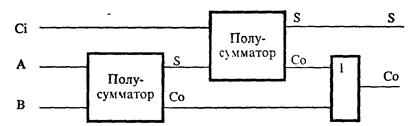
Рис. 4.24. Сумматор, составленный из двух полусумматоров
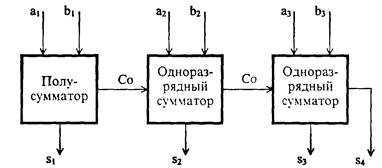
Рис. 4.25. Логическая схема суммирования двух трехразрядных двоичных чисел
Перейти к многоразрядным числам можно путем последовательного соединения соответствующего количества сумматоров. На рис. 4.25 представлена схема суммировання двух трехразрядных двоичных чисел А + В = S; в поразрядной записи эта-операция имеет следующие обозначения:
(a3a2a1) + (b3b2b1) = (S4S3S2S1)
Последовательность логических схем на рис. 4.23 - 4.25 отражает важнейшую в современной цифровой электронике и вычислительной технике идею последовательной интеграции. Такая интеграция позволяет реализовать все более функционально сложные узлы современного компьютера.
Дата добавления: 2015-10-13; просмотров: 850;
