Скалярное произведение векторов и его свойства

Лекция №5

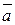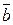Определение. Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними.

Обозначается 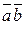, 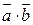(или 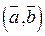). Итак, по определению,

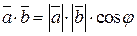, (6)

где .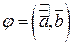

Формуле (6) можно придать иной вид. Так как ,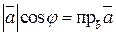

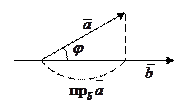
а 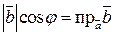, то получаем:

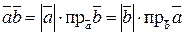, (7)

т.е. скалярное произведение двух векторов равно модулю одного из них, умноженному на проекцию другого на ось, сонаправленную с первым вектором.