Понятие энтропии. Вычисление изменения энтропии.

В начале лекции мы познакомились с понятием связанной энергии, то есть той части внутренней энергии, которую нельзя использовать для совершения работы. По ряду причин оказалось удобнее вместо связанной энергии ввести другую величину, которая называется энтропия и выражается формулой:

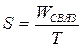(16)

то есть энтропия S – это величина связанной энергии, приходящаяся на единицу температуры (по шкале Кельвина). Размерность энтропии – Дж^.К ^–1. Очевидно, что W_СВЯЗ = T^.S, и U = G + W_СВЯЗ = G + T·S, откуда получаем связь между свободной энергией и энтропией: G = U – T· S (17).

Почти всегда при изучении конкретных процессов нас интересует не столько сама энергия, сколько её изменение. В биологической термодинамике мы чаще всего имеем дело с изотермическими процессами (температура тела постоянна). В этом случае: ΔG = ΔU – T·ΔS (18).

Вычисление изменения энтропии.

Рассмотрим сначала изотермические процессы, наиболее характерные для организма. Если изменение энтропии при переходе из состояния 1 в состояние 2 обозначить ΔS_1→2 ,то

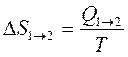, (19)

где Q_1→2 - это количество тепла, полученного системой в ходе обратимого перехода из первого состояния во второе.

Например, при плавлении 1 кг льда при 0⁰С в условиях, когда нет потерь тепла (и, значит, можно процесс считать обратимым), надо сообщить льду 335 кДж (эта величина называется удельной теплотой плавления). Поэтому в данном процессе изменение энтропии льда равно 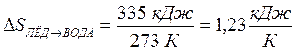, то есть при 0⁰С (273 К) энтропия 1 кг воды на 1,23 кДж/К больше, чем энтропия льда.

Если температура в ходе процесса изменяется, то изменение энтропии находится по более сложной формуле :

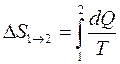(20)

(цифры 1 и 2 обозначают величины, характеризующие начальное и конечное состояния).

7. Второе начало термодинамики для изолированных систем.

Изолированныминазывают системы, которые не обмениваются с окружающей средой ни веществом, ни энергией. Абсолютно изолированных систем не бывает, но во многих случаях (например, для вещества в хорошем термосе) можно практически считать систему изолированной.

В изолированной системе общее изменение энтропии всегда положительно(то есть общая энтропия изолированной системы всегда возрастает).

Здесь важно не опустить слово „общее“. В какой-то части системы энтропия может уменьшиться, но это обязательно должно быть скомпенсировано увеличением энтропии в других частях системы.

Из формулы (18): ΔG = ΔU – T·ΔS видно, что если энтропия возрастает (ΔS > 0), то свободная энергия системы уменьшается (ΔG < 0). Поэтому второе начало можно сформулировать и по-другому: В изолированной системе общее изменение свободной энергии всегда отрицательно (то есть свободная энергия изолированной системы всегда уменьшается).

Эта формулировка более наглядна. Мы знаем, что во всех реальных процессах происходит диссипация свободной энергии, то есть часть свободной энергии превращается в связанную (преимущественно в тепловую). Если система изолированная, то извне свободная энергия не поступает, поэтому общий запас свободной энергии системы должен уменьшаться.

Второе начало термодинамики в приведенной формулировке имеет очень большое практическое значение, потому что оно позволяет точно установить, в каком направлении будет происходить тот или иной процесс. Например, если мы установим при расчёте, что при некотором процессе общая свободная энергия изолированной системы должна увеличиваться, можно категорически утверждать, что такой процесс невозможен.

Ещё чаще встречается такая ситуация: мы хотим провести некоторый физический или химический процесс в нужном нам направлении, и надо определить, при каких условиях это можно осуществить. В большинстве случаев применение второго начала термодинамики позволяет найти чёткий ответ на этот вопрос. Можно привести такой пример из техники. Для многих отраслец промышленности необходимо иметь в большом количестве алмазный инструмент. Природные алмазы слишком дороги, поэтому ещё в XIX веке пытались получить искусственные алмазы. Было потрачено много сил и средств, но эти попытки ни к чему не приводили, пока киевский физик Верещагин не провёл термодинамический расчёт и не определил условия, при которых графит может превращаться в алмаз. Условия оказались очень непростыми (температура не ниже 1000⁰С и давление не менее 150 тысяч атмосфер), но когда необходимые условия были чётко сформулированы, довольно быстро удалось наладить промышленное производство искусственных алмазов. Таких примеров можно привести много (в том числе из химических производств, технологии изготовления электронных приборов, ракетно-космической техники и т.п.).