Тема 3.4 Моделирование производственных и непроизводственных систем.

Для эффективной работы банка необходимы, во-первых, постоянное изучение и прогнозирование состояния рынка банковских услуг и, во-вторых, всестороннее планирование банковской деятельности и оперативное управление финансовыми ресурсами банка.

Банковские учреждения оказывают клиентам множество услуг, вступают в сложные взаимоотношения между собой и другими субъектами хозяйственной жизни, выполняют разнообразные функции. Для выживания в условиях обострившейся конкуренции банки должны искать пути совершенствования базовых технологий, внедрять новые банковские инструменты, поддерживать свою работу автоматизированной информационной системой управления и обработки данных, соответствующей международным требованиям и стандартам.

Моделирование банковских операций является одним из важных этапов анализа и оценки деятельности банка, а также разработки проекта автоматизированной банковской системы (АБС).

Отличительная черта российского финансового рынка — его субъективизм, крайняя зависимость от внеэкономических факторов и, как следствие, высокая степень неопределенности, которая затрудняет принятие обоснованных финансовых решений. Применение традиционных средств поддержки управленческих решений и прогнозирования в этих условиях затруднено, и тем ценнее возможность использования метода имитационного моделирования, повышенный интерес к которому проявляется сегодня в развитых странах. Этот метод воспринимается сегодня как мощный и перспективный инструмент конструирования и последующего исследования сложных бизнес-процессов и систем, в которых велико число переменных, трудоемок, а зачастую и невозможен математический анализ зависимостей, высок уровень неопределенности имитируемых ситуаций.

Распространению подобных моделей способствовал также коммерческий успех ряда аналитических программных продуктов, успешно используемых в банках, промышленных и торговых фирмах, государственных учреждениях, страховых компаниях и т.д. Практика применения имитационных моделей открыла новые возможности по концептуальному анализу проблем управления бизнесом, сокращению сроков разработки перспективных пилотных проектов, организации эффективного сопровождения сложных корпоративных приложений.

Сегодня подходы и методы имитационного моделирования могут оказаться чрезвычайно плодотворными в отечественных условиях перманентной экономической неустойчивости и риска. Прежде всего это касается перспективных, динамично развивающихся и находящихся в стадии становления активных секторов отечественного бизнеса, таких, как банковская и страховая деятельность, рынок информационных технологий, торгово-посреднический бизнес, а также рынок ценных бумаг.

Имитационная модель предназначена для имитации процесса функционирования реальных систем массового обслуживания. Системы массового обслуживания (СМО)представляют собой системы специального вида, реализующие многократное выполнение однотипных задач. Подобные системы играют важную роль во многих областях экономики, финансов, производства и быта. В качестве примеров СМО в финансово-экономической ; сфере можно привести банки различных типов (коммерческие, инвестиционные, ипотечные, инновационные, сберегательные), страховые организации, государственные акционерные общества, компании, фирмы, ассоциации, кооперативы, налоговые инспекции, аудиторские службы, различные системы связи (в том числе телефонные станции), погрузочно-разгрузочные комплексы (порты, товарные станции), автозаправочные станции, различные предприятия и организации сферы обслуживания (магазины, справочные бюро, парикмахерские, билетные кассы, пункты по обмену валюты, ремонтные мастерские, больницы). Такие системы, как компьютерные сети, системы сбора, хранения и обработки информации, транспортные системы, автоматизированные производственные участки, поточные линии, различные военные системы, в частности системы противовоздушной или противоракетной обороны, также могут ? рассматриваться как своеобразные СМО

Каждая СМО включает в свою структуру некоторое ; число обслуживающих устройств, которые называют каналами (приборами, линиями) обслуживания. Роль каналов могут играть различные приборы, лица, выполняющие те или иные операции (кассиры, операторы, парикмахеры, продавцы), линии связи, автомашины, краны, ремонтные бригады, железнодорожные пути, бензоколонки и т.д.

Системы массового обслуживания могут быть одноканальными или многоканальными.

Каждая СМО предназначена для обслуживания (выполнения) некоторого потока заявок (требований), поступающих на вход системы большей частью не регулярно, а случайные моменты времени. Обслуживание заявок, в этом случае, также длится не постоянное, заранее известное время, а случайное время, которое зависит от многиxслучайных, порой неизвестных нам, причин. После обслуживания заявки канал освобождается и готов к приему следующей заявки. Случайный характер потоказаявок и времени их обслуживания приводит к неравномерной загруженности СМО: в иное время на входе СМО могут скапливаться необслуженные заявки, что приводит к перегрузке СМО, а иногда при свободных каналах на входе СМО заявки не будет, что приводит к недогрузке СМО, т.е. к простаиванию ее каналов. Заявки, скапливающиеся на входе СМО, либо «становятся» в очередь, либо по причине невозможности дальнейшего пребывания в очереди покидают СМО необслуженными. Схема СМО изображена на рис.1.

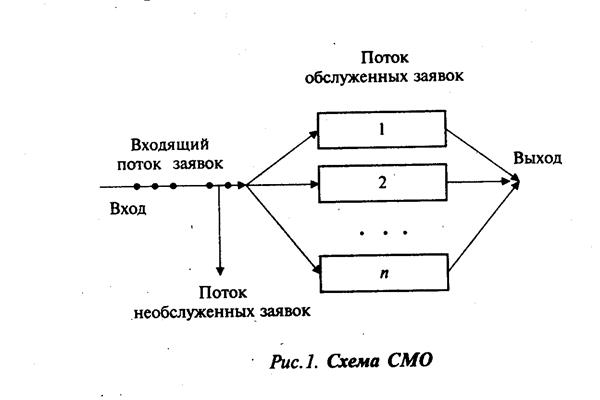
Таким образом, во всякой СМО можно выделить следующие основные элементы:

1) входящий поток заявок;

2) очередь;

3) каналы обслуживания;

4) выходящий поток обслуженных заявок.

Каждая СМО в зависимости от своих параметров — характера потока заявок, числа каналов обслуживания и их производительности, а также от правил организации работы обладает определенной эффективностью функционирования (пропускной способностью), позволяющей ей более или менее успешно справляться с потоком заявок.

Предметом изучения теории массового обслуживания •является СМО.

Цель теории массового обслуживания — выработка рекомендаций по рациональному построению СМО, рациональной организации их работы и регулированию потока заявок для обеспечения высокой эффективности функционирования СМО.

Для достижения этой цели решаются задачи теории массового обслуживания, состоящие в установлении зависимостей эффективности функционирования СМО I от ее организации (параметров): характера потока заявок, числа каналов и их производительности и правил работы СМО.

В качестве характеристик эффективности функционирования СМО можно, выбрать три основные группы (обычно средних) показателей:

1. Показатели эффективности использования СМО

• Абсолютная пропускная способность СМО — среднее число заявок, которое может обслужить СМО в единицу времени.

• Относительная пропускная способность СМО — отношение среднего числа заявок, обслуживаемых СМО в единицу времени, к среднему числу поступивших заявок за это же время.

• Средняя продолжительность периода занятости СМО.

• Коэффициент использования СМО — средняя доля времени, в течение которого СМО занята обслуживанием заявок, и т.п.

2. Показатели качества обслуживания заявок

• Среднее время ожидания заявки в очереди.

• Среднее время пребывания заявки в СМО.

• Вероятность отказа заявке в обслуживании без ожидания.

• Вероятность того, что поступившая заявка немедленно будет принята к обслуживанию.

• Закон распределения времени ожидания заявки в очереди.

• Закон распределения времени пребывания заявки в СМО.

• Среднее число заявок, находящихся в очереди.

• Среднее число заявок, находящихся в СМО, и т.п.

3. Показатели эффективности функционирования пары «СМО — потребитель», где под потребителем понимают всю совокупность заявок или некий их источник (например, средний доход, приносимый СМО в единицу времени, и т.п.)

Отметим, что третья группа показателей оказывается полезной в тех случаях, когда некоторый доход, получаемый от обслуживания заявок, и затраты на обслуживание измеряются в одних и тех же единицах. Эти показатели обычно носят вполне конкретный характер и определяются спецификой СМО, обслуживаемых заявок и дисциплиной обслуживания.

Случайный характер потока заявок и длительности их обслуживания порождает в СМО случайный процесс.

Случайным процессом (или случайной функцией) называется соответствие, при котором каждому значению аргумента (в данном случае — моменту из промежутка времени проводимого опыта) ставится в соответствие случайная величина (в данном случае — состояние СМО).

Случайной величиной называется величина, которая в результате опыта может принять одно, но неизвестное заранее, какое именно, числовое значение из данногочислового множества.

Для решения задач теории массового обслуживания необходимо этот случайный процесс изучить, т. е. построить и проанализировать его математическую модель.

Математическое изучение функционирования СМО значительно упрощается, если протекающий в ней случайный процесс является марковским. Случайный процесс, протекающий в СМО, называется марковским (или процессом без последействия, или процессом без памяти), если вероятность любого состояния СМО в будущем зависит только от ее состояния в настоящем и не зависит от.ее состояний в прошлом. В этом случае работа СМО сравнительно легко описывается с помощью аппарата конечных систем обыкновенных линейных дифференциальных уравнений первого порядка, а в предельном режиме (при достаточно длительном функционировании СМО) — с помощью аппарата конечных систем линейных алгебраических уравнений, и в результате удается выразить в явном виде основные характеристики эффективности функционирования СМО через параметры СМО, потока заявок и дисциплины работы СМО.

Чтобы случайный процесс был марковским, необходимо и достаточно, чтобы все потоки событий, под воздействием которых происходят переходы системы из состояния в состояние, были пуассоновскими, т.е. обладающими свойствами отсутствия последействия (для любых двух непересекающихся промежутков времени число событий, наступающих за один из них, не зависит от числа событий, наступающих за другой) и ординарностью (вероятность наступления за элементарный — малый промежуток времени более одного событий пренебрежимо мала по сравнению с вероятностью наступления за этот промежуток времени одного события). В СМО потоками событий являются потоки заявок, потоки «обслуживания» заявок и т.д.

Марковские системы массового обслуживания (СМО)

Допущения о пуассоновском характере потока заявок и о показательном распределении времени обслуживания ценны тем, что позволяют применить в теории массового обслуживания аппарат так называемых марковских случайных процессов.

Процесс, протекающий в физической системе, называется марковским (или процессом без последействия), если для каждого момента времени вероятность любого состояния системы в будущем зависит только от состояния системы в настоящий момент 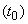и не зависит от того, каким образом система пришла в это состояние.

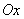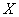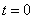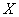Рассмотрим элементарный пример марковского случайного процесса. По оси абсцисс случайным образом перемещается точка . В момент времени точка находится в начале координат 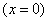и остается там в течение одной секунды. Через секунду бросается монета; если выпал герб - точка 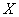перемещается на одну единицу длины вправо, если цифра - влево. Через секунду снова бросается монета и производится такое же случайное перемещение, и т. д. Процесс изменения положения точки (или, как говорят, «блуждания») представляет собой случайный процесс с дискретным временем 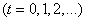и счетным множеством состояний

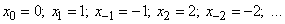
Схема возможных переходов для этого процесса показана на рис. 19.7.1.

Рис. 19.7.1.

Покажем, что этот процесс - марковский. Действительно, представим себе, что в какой-то момент времени 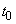система находится, например, в состоянии 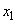- на одну единицу правее начала координат. Возможные положения точки через единицу времени будут 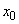и 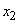с вероятностями 1/2 и 1/2; через две единицы - 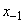, , 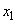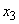с вероятностями 1/4, ½, 1/4 и так далее. Очевидно, все эти вероятности зависят только от того, где находится точка в данный момент 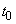, и совершенно не зависят от того, как она пришла туда.

Рассмотрим другой пример. Имеется техническое устройство 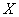, состоящее из элементов (деталей) типов 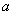и 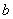, обладающих разной долговечностью. Эти элементы в случайные моменты времени и независимо друг от друга могут выходить из строя. Исправная работа каждого элемента безусловно необходима для работы устройства в целом. Время безотказной работы элемента - случайная величина, распределенная по показательному закону; для элементов типа 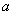и 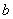параметры этого закона различны и равны соответственно 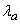и 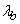. В случае отказа устройства немедленно принимаются меры для выявления причин и обнаруженный неисправный элемент немедленно заменяется новым. Время, потребное для восстановления (ремонта) устройства, распределено по показательному закону с параметром 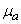(если вышел из строя элемент типа 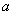) и 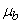(если вышел из строя элемент типа ).

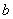В данном примере случайный процесс, протекающий в системе, есть марковский процесс с непрерывным временем и конечным множеством состояний:

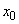- все элементы исправны, система работает,

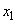- неисправен элемент типа 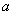, система ремонтируется,

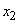- неисправен элемент типа 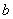, система ремонтируется.

Схема возможных переходов дана на рис. 19.7.2.

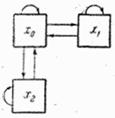
Рис. 19.7.2.

Действительно, процесс обладает марковским свойством. Пусть например, в момент 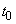система находится в состоянии 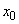(исправна). Так как время безотказной работы каждого элемента - показательное, то момент отказа каждого элемента в будущем не зависит от того, сколько времени он уже работал (когда поставлен). Поэтому вероятность того, что в будущем система останется в состоянии 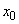или уйдет из него, не зависит от «предыстории» процесса. Предположим теперь, что в момент 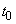система находится в состоянии 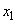(неисправен элемент типа 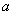). Так как время ремонта тоже показательное, вероятность окончания ремонта в любое время после 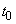не зависит от того, когда начался ремонт и когда были поставлены остальные (исправные) элементы. Таким образом, процесс является марковским.

Заметим, что показательное распределение времени работы элемента и показательное распределение времени ремонта - существенные условия, без которых процесс не был бы марковским. Действительно, предположим, что время исправной работы элемента распределено не по показательному закону, а по какому-нибудь другому - например, по закону равномерной плотности на участке 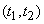. Это значит, что каждый элемент с гарантией работает время 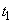, а на участке от 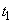до 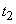может выйти из строя в любой момент с одинаковой плотностью вероятности. Предположим, что в какой-то момент времени 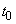элемент работает исправно. Очевидно, вероятность того, что элемент выйдет из строя на каком-то участке времени в будущем, зависит от того, насколько давно поставлен элемент, т. е. зависит от предыстории, и процесс не будет марковским.

Аналогично обстоит дело и с временем ремонта 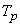; если оно не показательное и элемент в момент 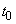ремонтируется, то оставшееся время ремонта зависит от того, когда он начался; процесс снова не будет марковским.

Вообще показательное распределение играет особую роль в теории марковских случайных процессов с непрерывным временем. Легко убедиться, что в стационарном марковском процессе время, в течение которого система остается в каком-либо состоянии, распределено всегда по показательному закону (с параметром, зависящим, вообще говоря, от этого состояния). Действительно, предположим, что в момент 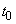система находится в состоянии и до этого уже находилась в нем какое-то время. Согласно определению марковского процесса, вероятность любого события в будущем не зависит от предыстории; в частности, вероятность того, что система уйдет из состояния в течение времени 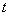, не должна зависеть от того, сколько времени система уже провела в этом состоянии. Следовательно, время пребывания системы в состоянии должно быть распределено по показательному закону.

В случае, когда процесс, протекающий в физической системе со счетным множеством состояний и непрерывным временем, является марковским, можно описать этот процесс с помощью обыкновенных дифференциальных уравнений, в которых неизвестными функциями являются вероятности состояний 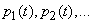. Составление и решение таких уравнений мы продемонстрируем в следующем на примере простейшей системы массового обслуживания.