ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ - это система счисления, в которой величина, обозначаемая цифрой, зависит от места (позиции) цифры в числе.

Например: рассмотрим три числа 298, 829, 982.

Эти числа, разуется, различны, хотя в их записи участвуют одни и те же цифры. Различаются же записи расположением цифр – иными словами, тем, какую позицию занимает та или иная цифра. Отсюда и пошло название такой нумерации – позиционная.

►Примером позиционной системы счисления является десятичная. Причины, по которой она оказалась общепринятой, совсем не математического характера. Десять пальцев рук - вот тот первоначальный аппарат для счета, которым человек пользовался с доисторических времен. По пальцам удобно считать от одного до десяти. Сосчитав до десяти, т.е. использовав до конца возможности нашего природного «счетного аппарата», естественно принять само число 10 за новую, более крупную единицу (единицу следующего разряда).

На рис. 4 изображено древнее написание десятичных цифр. Каждая цифра обозначает число по количеству углов в ней: 0 – нет углов, 1 – один угол, 2 – два угла и т.д.

Написание десятичных цифр претерпело существенные изменения. Формой, которой мы пользуемся, установилась в XVI веке.

Исторически десятичная система счисления сложилась и развивалась в Индии. Европейцы заимствовали индийскую систему счисления у арабов, назвав ее арабской. Это исторически неправильное название удерживается и поныне. Возникновение и развитие десятичной системы счисления явилось одним из важнейших достижений человеческой мысли (наряду с появлением письменности).

Однако десятичной системой счисления люди пользовались не всегда. В разные исторические периоды многие народы использовали другие системы счисления.

►Довольно широкое распространение имела двенадцатеричная система счисления. Вместо, того, чтобы сказать «двенадцать», мы иногда говорим «дюжина»

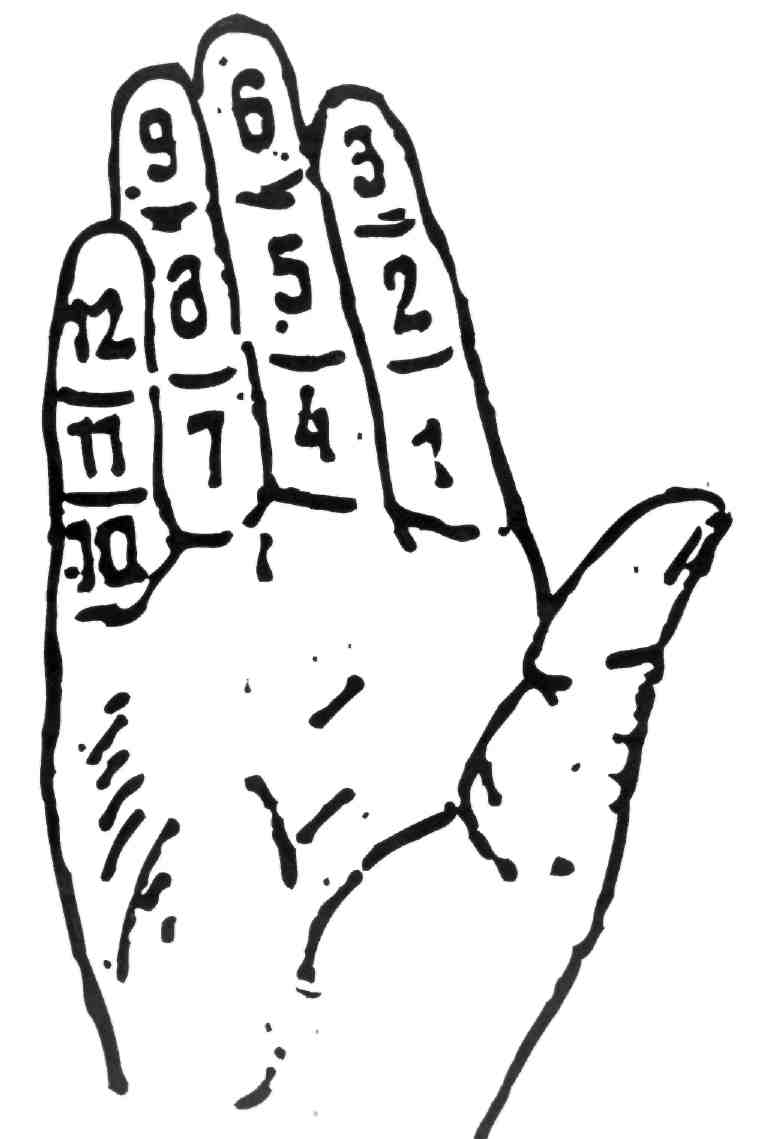Происхождение ее тоже связано со счетом на пальцах. Считали большой палец руки и фаланги остальных четырех пальцев: всего 12 (рис. 5).

Элементы двенадцатеричной системы счисления сохранились в Англии в системе мер: 1 фут=12 дюймов, в денежной системе 1 шиллинг = 12 пенсов (1 дюйм =1/12 фута=2,54 см; 1 фут = 30,48 см).

Нередко и мы сталкиваемся с этой системой в быту: чайные и столовые сервизы на 12 персон, комплект носовых платков – 12 штук.

► Пятеричная система счисления по свидетельству известного исследователя Африки Стэнли, у ряда африканских племен она была распространена. Долгое время пятеричной системой счисления пользовались и в Китае. Очевидна связь этой системы со строением человеческой руки.

►Двадцатеричная система счисления была принята у ацтеков и майя – народов, населявших в течение многих столетий обширные области Американского континента и создавшие там высочайшую культуру, в том числе и математическую. Также 20-ричная система счисления была принята у кельтов, населявших Западную Европу, начиная со второго тысячелетия до н.э.

Основу для счета в этой системе счисления составляли пальцы рук и ног. Некоторые следы 20-ричной системы счисления кельтов сохранились во французской денежной системе. Основная денежная единица – франк делится на 20 (1 франк = 20 су).

►Шестидесятеричная система счисления или так называемая «вавилонская» весьма сложная система, существовавшая в Древнем Вавилоне.

Мнения историков по поводу того, как именно возникла эта система счисления, расходятся. Существуют две гипотезы: 1) слияние двух племен, одно из которых пользовалось шестеричной, а другое десятичной. Т.е. она возникла в результате политического компромисса. 2) древние вавилоняне считали продолжительность года равной 360 суткам, что естественно связано с числом 60.

Отголосками использования этой системы счисления дошли до наших дней 1 час = 60 мин., 1⁰ = 60’. В целом 60-ричная система счисления громоздка и неудобна.

Итак, рассмотрим обобщенную схему классификации групп систем счисления рис. 7.

Давайте подробнее остановимся на «машинной» группе систем счисления.

►В последнее время с десятичной системой счисления серьезно конкурирует двоичная система счисления, которой предпочитают пользоваться современные вычислительные машины.

Обработка информации в ЭВМ основана на обмене электрическими сигналами между различными устройствами машины. Эти сигналы возникают в определенной последовательности. Признак наличия сигнала можно обозначить цифрой 1, а признак отсутствия сигнала – цифрой 0. Т.о., в ЭВМ реализуется два устойчивых состояния. С помощью определенных наборов цифр 0 и 1 можно закодировать любую информацию. Каждый такой набор нулей и единиц называется двоичным кодом.

Широкое распространение получила так называемая колировка ASCII (American Standard Code for Information Interchange – американский стандартный код для обмена информацией). Это семиразрядный код (каждый символ кодируется семью разрядами) – т.о. можно всегда закодировать 128 символов (7 разрядов по 2 цифры дают 2*2*2*2*2*2*2=128 вариантов записей числа).

Мы обычно пользуемся восьмиразрядным расширением кода ASCII . За счет добавления «лишнего» разряда можно получить еще 128 символов, всего их становится 256. Это расширение позволяет кодировать буквы русского алфавита и некоторые специальные символы.

Самая замечательная(для компьютера) система счисления – двоичная. В ней используется только две цифры – 0 и 1. Она проста, и поэтому интересна.

Стоит отметить, что двоичная система счисления издавна была предметом пристального внимания многих ученых.

Вот, что писал П.С. Лаплас об отношении к двоичной (бинарной) системе великого немецкого математика Г.Ф. Лейбница: «В своей бинарной арифметике Лейбниц видел прообраз творения. Ему представлялось, что единица представляет божественное начало, а нуль – небытие, и что высшее существо создает все сущее из небытия точно таким же образом, как единица и нуль в его системе выражают все числа».

Эти слова подчеркивают удивительную универсальность алфавита, состоящего всего из двух символов.

Самый существенный недостаток двоичной системы счисления – числа в этой системе гораздо длиннее, чем в десятичной.