Контроль целостности компонентов компьютерной системы

Контроль целостности программ и данных выполняется одни­ми и теми же методами. Исполняемые программы изменяются крайне редко на этапе их эксплуатации. Существует достаточно широкий класс программ, для которых все исходные данные или их часть также изменяются редко. Поэтому контроль целостности таких файлов выполняется так же, как и контроль программ.

Контроль целостности программных средств и данных осуще­ствляется путем получения (вычисления) характеристик и сравне­ния их с контрольными характеристиками. Контрольные характе­ристики вычисляются при каждом изменении соответствующего файла. Характеристики вычисляются по определенным алгорит­мам. Наиболее простым алгоритмом являетсяконтрольное сум­мирование. Контролируемый файл в двоичном виде разбивается на слова, обычно состоящие из четного числа байт. Все двоичные слова поразрядно суммируются с накоплением по mod2, образуя в результате контрольную сумму. Разрядность контрольной суммы равняется разрядности двоичного слова. Алгоритм получения контрольной суммы может отличаться от приведенного, но, как правило, не является сложным и может быть получен по имею­щейся контрольной сумме и соответствующему файлу.

Другой подход к получению характеристик целостности свя­зан с использованиемциклических кодов. Суть метода со­стоит в следующем. Исходная двоичная последовательность представляется в виде полинома F(x) степени п-1, где n - число бит последовательности. Для выбранного порождающего поли­нома Р(х) можно записать равенство:

F(x) • х"= G(x) -Р(х) © R(x),

где m - степень порождающего полинома, G(x) - частное, a R(x) -остаток от деления F(x) • х°³ на Р(х).

Из приведенного соотношения можно получить новое выра­жение:

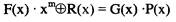
Из последнего выражения можно сделать вывод: если исход­ный полином увеличить на х" (сдвинуть в сторону старших раз­рядов на m разрядов) и сложить с остатком R(x) по модулю 2, то полученный многочлен разделится без остатка на порождающий полином Р(х).

При контроле целостности информации контролируемая по­следовательность (сектор на диске, файл и т. д.), сдвинутая на m разрядов, делится на выбранный порождающий полином, и запо­минается полученный остаток, который называют синдромом. Синдром хранится как эталон. При контроле целостности к поли­ному контролируемой последовательности добавляется синдром и осуществляется деление на порождающий полином. Если остаток от деления равен нулю, то считается, что целостность контроли­руемой последовательности не нарушена. Обнаруживающая спо­собность метода зависит от степени порождающего полинома и не зависит от длины контролируемой последовательности. Чем выше степень полинома, тем выше вероятность определения из­менений d, которая определяется из соотношения: d =1/2¹¹¹.

Использование контрольных сумм и циклических кодов, как и других подобных методов, имеет существенный недостаток. Ал­горитм получения контрольных характеристик хорошо известен, и поэтому злоумышленник может произвести изменения таким об­разом, чтобы контрольная характеристика не изменилась (напри­мер, добавив коды).

Задача злоумышленника усложнится, если использовать пере­менную длину двоичной последовательности при подсчете кон­трольной характеристики, а характеристику хранить в зашифро­ванном виде или вне КС (например, в ЗУ Touch Memory).

Рассмотрим пример использования циклических кодов для контроля целостности двоичной последовательности.

Пусть требуется проконтролировать целостность двоичной последовательности А= 1010010. Используется порождаемый по­лином вида: P(x)^:=x^з+x+l.

А. Получение контрольной характеристики

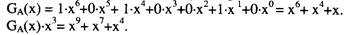
При вычислении синдрома Кд(х) действия выполняются по правилам деления полиномов, заменяя операцию вычитания опе­рацией сложения по модулю:

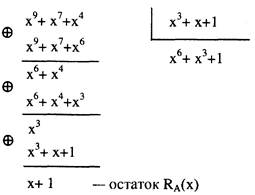
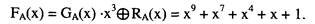
Двоичная последовательность с синдромом имеет вид :

А' = 1010010011 (синдром подчеркнут). Последовательность А' хранится и(или) передается в КС.

Б. Контроль целостности информации.

Если изменений последовательности А' = 1010010011 не про­изошло, то соответствующий ей полином должен разделиться на порождающий полином без остатка:

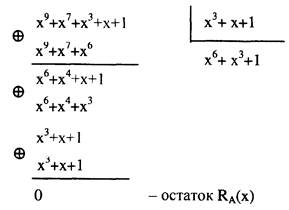
Результат произведенных вычислений свидетельствует о це­лостности информации.

Если синдром отличен от нуля, то это означает, что произошла ошибка при хранении (передаче) двоичной последовательности. Ошибка определяется и в контрольных разрядах (в синдроме).

Существует метод, который позволяет практически исключить возможность неконтролируемого изменения информации в КС. Для этого необходимо использовать хэш-функцию. Подхэш-функцией понимается процедура получения контрольной харак­теристики двоичной последовательности, основанная на кон­трольном суммировании и криптографических преобразованиях. Алгоритм хэш-функции приведен в ГОСТ Р34.11-94. Алгоритм не является секретным, так же как и алгоритм используемого при получении хэш-функции криптографического преобразования, изложенного в ГОСТ 28147-89 [9].

Исходными данными для вычисления хэш-функции являются исходная двоичная последовательность и стартовый вектор хэши­рования. Стартовый вектор хэширования представляет собой дво­ичную последовательность длиной 256 бит. Он должен быть не­доступен злоумышленнику. Вектор либо подвергается зашифро­ванию, либо хранится вне КС.

Итерационный процесс вычисления хэш-функции Н преду­сматривает:

• генерацию четырех ключей (слов длиной 256 бит);

• шифрующее преобразование с помощью ключей текущего значения Н методом простой замены (ГОСТ 28147-89);

• перемешивание результатов;

• поразрядное суммирование по mod2 слов длиной 256 бит ис­ходной последовательности;

• вычисление функции Н.

В результате получается хэш-функция длиной 256 бит. Значе­ние хэш-функции можно хранить вместе с контролируемой ин­формацией, т. к., не имея стартового вектора хэширования, зло­умышленник не может получить новую правильную функцию хэширования после внесения изменений в исходную последова­тельность. А получить стартовый вектор по функции хэширова­ния практически невозможно.

Для каждой двоичной последовательности используются две контрольные характеристики: стартовый вектор и хэш-функция. При контроле по стартовому вектору и контролируемой последовательности вычисляется значение хэш-функции и сравнивается с контрольным значением.