Покрытия с цилиндрически оболочками и призматическими складками

Покрытие с применением цилиндрических оболочек образуется из тонких плит, изогнутых по цилиндрической поверхности, бортовых элементов и торцевых диафрагм. По углам покрытия поддерживается колоннами (рис.65).

Рис. 65. Типы цилиндрических оболочек:

а - однопролетная; б - многопролетная; в – многоволновая

Вид цилиндрических оболочек обуславливается соотношением их пролета l₁ (расстояние между диафрагмами) и длины волны l₂ (расстояние между бортовыми элементами). При l₁/l₂>1 оболочки называют длинными; при l₁/l₂<1 - короткими.

Очертания плиты оболочки в поперечном сечении чаще применяют круговым. Высота поперечного сечения оболочки h₁=(1/5-1/10)l₁ включает в себе высоту волны h₃₌(1/8-1/6)l₂ и бортовых элементов h₂₌(1/30-1/20)l₁ . Толщина плиты монолитных оболочек не менее 5 см; сборных ребристых - не менее 3 см.

1.Длинные оболочки

По расчету цилиндрических оболочек проведено много исследований, которые свидетельствуют, что расчет по прочности длинных одноволновых и многоволновых цилиндрических оболочек может быть выполнен раздельно в продольном (пролетном) и поперечном (волновом) направлениях.

Если на покрытие действует равномерно распределенная нагрузка, и оно в целом оперто по углам при отношении размеров в плане l₁/l₂>3 расчет по прочности, жесткости и трещиностойкости оболочки в направлении пролета производят как балки корытообразного профиля (рис.66) [21].

Условие прочности получают из рассмотрения равенства внешних сил и внутренних усилий относительно центра круговой части сечения

,

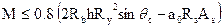где М - момент внешних сил, 0,8 - дополнительный коэффициент условия работы; h,R_y - толщина и радиус цилиндрической части оболочки; q_c - половина центрального угла дуги сжатой зоны; a₀ - расстояние от равнодействующей усилий в растянутой арматуре до центра кривизны круговой части сечения оболочки (рис.66).

Рис. 66. К расчету длинной цилиндрической оболочки в направлении пролета как железобетонной балки по стадии предельного равновесия (а) и в направлении волны как пространственной полосы (б,в,г):

б - поперечная полоса оболочки единичной длины с действующими на ней касательными силами; в - часть поперечной полосы оболочки с действующими на нее нагрузкой, силами и моментом; г - очертание эпюры изгибающих моментов, действующих в направлении волны

Положение нейтральной оси определяют из условия равенства нулю проекций всех действующих в сечении сил на горизонтальную ось

.

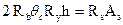По результатам статического расчета подбирают сечение арматуры оболочки. Оба выражения объединяются в одно, приняв sinq_c@q_c. Примерно 80% рабочей растянутой арматуры (Тип I) помещают в бортовых элемента (рис. 67). При пролетах ℓ₁>18м для бортовых элементов рекомендуют применять напрягаемую арматуру.

Рис. 67. Схемы армирования длинной оболочки:

а - оболочка; б - армирование оболочки вблизи промежуточного бортового элемента; в - то же, над промежуточной диафрагмой

Касательные усилия в оболочке достигают наибольшего значения на опоре, в придиафрагменной зоне, их находят по формуле сопротивления материалов

,

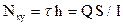где Q - поперечная сила в опорном сечении оболочки, вычисленная как для простой балки; S и I - геометрические характеристики сечения относительно горизонтальной оси, проходящей через центр круговой части сечения, τ - касательные напряжения в оболочке.

Расчет по прочности оболочек в направлении волны на поперечные изгибающие моменты M_y и сдвигающие усилия производят из условия равновесия элементарной полосы, вырезанной по длине оболочки (рис. 66). Полоса находится под действием внешней вертикальной нагрузки q, веса оболочки и касательной сил τh и τh +Dτh .

Сдвигающие усилия, действующие в срединной поверхности оболочки, передаются на диафрагмы. Статический расчет диафрагм состоит в определении внутренних усилий M,N и Q от действия N_xy с учетом конструктивных особенностей диафрагмы и ее собственного веса.

В сборных покрытиях с длинными цилиндрическими оболочками применяют два варианта разрезки на сборные элементы, когда оболочка монолитно связана с бортовыми элементами и когда отделена от бортовых элементов (рис.68).

Рис. 68. Конструктивные схемы сборных покрытий с длинными цилиндрическими оболочками:

а - оболочка монолитно соединена с бортовыми элементами; б - оболочка отделена от бортовых элементов; 1 - затяжка диафрагмы; 2 - сборная панель; 3 - арматура (предварительно напряженная); 4 - стыковая накладка; 5 - бортовой элемент

2. Короткие оболочки

Цилиндрические оболочки и складки называют короткими, если отношение их размеров в плане ℓ₁/ℓ₂<1 (рис.69). Толщину плиты принимают равной 5-6 см при ℓ₁=6 м и 7-8 см при ℓ₁=9 или 12 м. Класс бетона В20-В30. Плиту армируют конструктивной сеткой из стержней 5….6 мм с шагом 100-200 мм. Наиболее часто в практике строительства встречаются короткие оболочки с размерами в плане ℓ₁/ℓ₂£0.5.

Рис. 69. Конструктивная схема монолитной короткой цилиндрической оболочки:

1 - цилиндрическая плита; 2 - бортовой элемент; 3 - диафрагма

Такие оболочки рассчитывают упрощенным способом, позволяющим раздельно вычислять усилия в плитах, бортовых элементах и диафрагмах. Плиту рассчитывают как однопролетную балку криволинейного сечения пролетом l₁ и шириной l₂ , опирающуюся на диафрагмы. Так как изгибающий момент в середине пролета

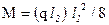
и средняя величина плеча внутренней пары усилий z»0,55h=0,55(f+h₂), то необходимое сечение продольной растянутой арматуры

,

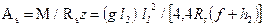где 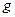- расчетная нагрузка на 1 м² горизонтальной проекции оболочки с учетом веса бортовых элементов высотой 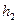. Эту арматуру укладывают в бортовые элементы. Поперечную арматуру ставят конструктивно. Вблизи бортовых элементов и над диафрагмами ставят дополнительные сетки (рис. 70).

Рис. 70. Детали армирования монолитных коротких оболочек у бортовых элементов (а) над промежуточными диафрагмами (б) и расчетная схема диафрагмы короткой оболочки (в):

1 - сварные каркасы; 2 - дополнительные сварные сетки

В направлении ℓ₂ диафрагму рассчитывают во взаимодействии с плитой оболочки.

К сборным предварительно напряженным коротким цилиндрическим оболочкам относятся крупноразмерные железобетонные сводчатые панели КЖС размерами в плане 3х12; 3х18; 3х24м. Бетон классов В25÷В45. Основная арматура небольших панелей предварительно напрягаемая классов А-IV и А-IIIв. Диафрагмы панелей длиной ℓ₂³18м армируют канатами К-7 или высокопрочной проволокой Вр-II [12]. Бортовые элементы армируют сварными каркасами из стали класса А-III, плиту оболочек - сетками из арматуры класса Вр-1. Примеры расчета КЖС приведены в [4,14,15,21].

3.Призматические складки

Покрытия с применением призматических складок образуются из плоских плит-граней (монолитно связанных по ребрам), бортовых элементов и диафрагм (рис. 71).

Рис. 71. Покрытия с призматическими складками:

а - типы поперечных сечений и диафрагм; б - расчетная схема складки в направлении волны; 1 - складка; 2- бортовой элемент; 3 - шпренгельная диафрагма; 4 - балочная диафрагма

Расчет в направлении ℓ₁ ведется аналогично расчету длинных цилиндрических оболочек, в направлении ℓ₂ - как многопролетной балочной плиты с ломаной осью. Ширина граней 3÷3,5 м. В трехгранных складках длина волны ℓ₂=9÷12 м.

Грани складки армируют вдоль волны согласно с эпюрами моментов многопролетных плит. Растянутую продольную арматуру складки в направлении ℓ₁ располагают в бортовых элементах. Продольную сжатую арматуру граней вдоль ℓ₂ ставят конструктивно из стержней диаметром 5-8 мм с шагом 200-250 мм.

Купола

Купола применяют для покрытия круглых в плане зданий и сооружений диаметром до 100 м, таких как цирки, резервуары, выставочные павильоны и т.п. Купольное покрытие состоит из двух основных конструктивных элементов: оболочки и опорного кольца. Для верхнего естественного освещения в куполе дополнительно устраивают верхнее фонарное кольцо. По расходу материалов купола более экономичны, чем другие пространственные покрытия. Чаще всего применяются сферические оболочки, образованные вращением вокруг вертикальной оси дуги круга. Оболочки куполов могут быть монолитными гладкими или сборными ребристыми. Монолитные купола имеют гладкую оболочку вращения, толщиной h≤50 мм (рис. 72).У мест примыкания к опорному кольцу оболочка утолщается.

Рис. 72. Конструкция монолитного (а) и сборного (б) купола:

1 - монолитная оболочка купола; 2 - сборная плита купола; 3 - опорное кольцо; 4 - фонарное кольцо; 5 - рабочая ненапрягаемая арматура; 6 - канаты; 7 - выступ опорного кольца

В настоящее время применяют в основном купола со сборными оболочками. Разрезка оболочки на элементы может быть меридиональной (для небольших куполов) или меридионально-кольцевой. В обоих случаях сборные элементы ребристые. Элементы большой длины криволинейные, малой длины - плоские. Опорное кольцо может быть сборным и монолитным.

В тонкостенном куполе при равномерно распределенной нагрузке на большей части оболочки развивается безмоментное напряженное состояние. Полное напряженное состояние - лишь вблизи опорного кольца. Кольцевыми изгибающими моментами M₂ можно пренебречь. Поэтому тонкостенная оболочка с непрерывным по контуру шарнирно-подвижными опорами, совпадающими по направлению с касательной к оболочке, может быть рассчитана по безмоментной теории. Элемент оболочки, ограниченный двумя меридиональными и двумя кольцевыми сечениями находится под воздействием усилий N₁, N₂ и S (рис. 73).

а - схема купола с шарнирно-подвижным опиранием по контуру; б - часть купола, отделенная плоскостью, параллельной основанию; в - элемент купола с действующими на него внутренними усилиями; 1 – меридиональное сечение; 2 – кольцевое сечение; 3 – тангенциальные опоры по периметру

Рис. 74. Шаровой статически определимый купол:

а - расчетная схема; б, в, - эпюры усилий N₁ и N₂ в полусферическом куполе от веса покрытия

Согласно расчетной схеме, приведенной на рис. 74,а из условия равновесия сегмента купола, можно записать

,

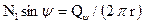где r - радиус кольцевого сечения, Q_ψ - нагрузка на сегмент купола, ограниченный углом ψ; N₁ - меридиональное усилие, отнесенное к единице длины сечения. Меридиональное усилие

.

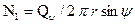Горизонтальная проекция меридионального усилия N₁, называемая распором H₁, равна:

.

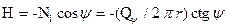Уравнение равновесия купола

,

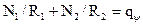где R₁ - радиус кривизны оболочки по меридиональному сечению; R₂ - то же по кольцевому; q_ψ - составляющая нагрузки, нормальная к поверхности купола, 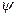– текущая угловая координата.

Зная усилие N₁ можно определить кольцевое усилие

.

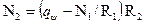Из этих уравнений видно, что в меридиональном направлении оболочка вращения во всех точках испытывает сжатие. В кольцевом направлении оболочка в верхней зоне сжата, в нижней - растянута, так как соотношение N₁/r₁, может быть как меньше, так и больше q_ψ.

В реальных конструкциях оболочка купола имеет не безмоментное опирание, а упругое закрепление в опорном кольце. Поэтому по линии контакта оболочки и кольца возникают дополнительно статически неопределимые величины - меридиональный изгибающий момент M₀ и радиальный распор H₀. Их определяют из условия совместности деформаций оболочки и опорного кольца купола (рис.75).

Рис. 75. К расчету купола, упругозакрепленного по контуру:

а - расчетная схема купола; б - расчетная схема опорного узла; в- положительные направления угловых и радиальных перемещений оболочки и опорного кольца; 1 – купол; 2 – опорное кольцо

Как видно из рис.76 по мере удаления от опорного кольца изгибающий момент уменьшается, меняет знак и затухает.

Рис. 76. Эторы моментов и кольцевых усилий в куполе, упругозакрепленном по контуру

От воздействия распора H₀ на опорное кольцо (рис. 77, а) в нем возникает растягивающее усилие N_Н^k, которое вызывает радиальное перемещение оси кольца. Распор H₀ приложен к кольцу с эксцентриситетом e , образуя момент H₀e и кольцо поворачивается на угол q_h^k. От воздействия момента M₀, равномерно распределенного вдоль кольца в радиальном направлении возникает момент в кольцевом направлении М=М₀r₀, а его поперечные сечения поворачиваются на угол q_м^k. Опорное кольцо находится в условиях внецентренного растяжения. Вследствие малости изгибающего момента его можно рассчитывать как центрально- растянутое.

а – распора; б - моментов

Оболочка монолитного купола, за исключением приопорных зон, сжата, армируется конструктивно одиночной сеткой из стержней диаметром 5-6 мм с шагом 150-200 мм. При толщине оболочки h³80мм ставят двойную сетку. У опорного кольца ставят дополнительную меридиональную арматуру на восприятие опорного момента M_x из стержней диаметром 6-8мм и дополнительную кольцевую арматуру для восприятия N₂. Рабочую арматуру опорного кольца ставят в виде кольцевых стержней диаметром 20-30 мм, стыкуемых на сварке, чаще опорные кольца куполов подвергают предварительному обжатию посредством натяжения кольцевой рабочей арматуры (рис. 78).

Рис. 78. Детали армирования монолитных куполов:

а - при обычном армировании; б - с предварительным напряжением кольцевой арматуры; 1 - рабочая арматура опорного кольца; 2 - дополнительная арматура по расчету на M_x; 3 - конструктивная сетка, укладываемая по всей области оболочки; 4 - кольцевая арматура по расчету на N₂; 5 - напрягаемая арматура; 6 - торкретная штукатурка

Напрягаемая арматура опорного кольца анкеруется на его выступах, расположенных по периметру в четырех, восьми и более местах в зависимости от диаметра кольца (рис. 72).