Массивы и вложение операторов цикла

Массивы и переменные с индексами. Математическим по­нятием, которое привело к появлению в языках программирования понятия "массив", являются матрица и ее частные случаи: вектор-столбец или вектор-строка. Элементы матриц в математике принято обозначать с использованием индексов. Существенно, что все элементы матриц либо вещественные, либо целые и т.п. Такая "однородность" элементов свойственна и массиву, определение которого описывает тип элементов, имя массива и его размерность, т.е. число индексов, необходимое для обозначения конкретного элемента. Кроме того, в определении указывается количество значений, принимаемых каждым индексом. Например, int a[10]; определяет массив из 10 элементов а[0], а[1], ..., а[9]. float Z[13][[6]; определяет двумерный массив, первый индекс которого принимает 13 значений от 0 до 12, второй индекс принимает 6 значений от 0 до 5. Таким образом, элементы двумерного массива Z можно перечислить так:

Z[0][0], Z[0] [1], Z[0][2],...,Z[12][4], Z[12][5]

В соответствии с синтаксисом Си в языке существуют только одномерные массивы, однако элементами одномерного массива, в свою очередь, могут быть массивы. Поэтому двумерный массив определяется как массив массивов. Таким образом, в примере определен массив Z из 13 элементов-массивов, каждый из которых, в свою очередь, состоит из 6 элементов типа float. Нумерация элементов любого массива всегда начинается с 0, т.е. индекс изменяется от 0 до N-1, где N -количество значений индекса.

Ограничений на размерность массивов, т.е. на число индексов у его элементов, в языке Си теоретически нет. Стандарт языка Си требует, чтобы транслятор мог обрабатывать определения массивов с размерностью до 31. Однако чаще всего используются одномерные и двумерные массивы. Рассмотрим на простых вычислительных задачах некоторые приемы работы с массивами.

Вычисление среднего. Введя значение n из диапазона (0<n<=100) и значения n первых элементов массива х[0], х[1],...,х[n-1], вычислить среднее и оценку дисперсии значений введенных элементов массива. Задачу решает следующая программа:

/* Вычисление среднего */

#include <stdio.h>

void main ( )

{ /*n - количество элементов */

int i,n;/*b-среднее */

float b,x[100];

while (1)

{

printf("\n Введите Значение n=");

scanf("%d", &n);

if ( n > 0 && n <= 100 ) break;

printf("\n Ошибка! Необходимо 0<n<101 ") ;

} /* Конец цикла ввода значения n */

printf("\n Введите Значения элементов:\n");

for( b=0.0,i=0; i<n; i++)

{

printf("x[%d] =", i);

scanf("%f", &x[i]);

b+=x[i]; /* Вычисление суммы элементов */

}

b/=n;/* Вычисление среднего */

printf("\n Среднее =%f, b) ;

}

В программе определен массив х со 100 элементами, хотя в каждом конкретном случае используются только первые n из них. Ввод значения п сопровождается проверкой допустимости вводимого значения. В качестве условия после while записано заведомо истинное выражение 1, поэтому выход из цикла (оператор break) возможен только при вводе правильного значения n, удовлетворяющего неравенству 0<n<101. Следующий цикл обеспечивает ввод n элементов массива и получение их суммы (b).

Вложенные циклы. В теле цикла разрешены любые исполнимые операторы, в том числе и циклы, т.е. можно конструировать вложенные циклы.

В качестве примера рассмотрим фрагмент программы для получения суммы такого вида:

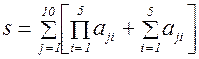
Введем следующие обозначения: а - двумерный массив, содержащий значения элементов матрицы; р - произведение элементов строки матрицы; с - сумма их значений; s - искомая сумма (результат). Опустив определения переменных и операторы ввода-вывода, запишем текст на языке Си:

double a[10][5];

for( s=0.0,j=0; j<10; j++)

{

for( p=1.0,c=0.0,i=0; i<5; i++)

{

p*=a[j][i];

c+=a[j][i];

}

s+=c+p;

}

При работе с вложенными циклами следует обратить внимание на правила выполнения операторов break и continue. Каждый из них действует только в том операторе, в теле которого он непосредственно использован. Оператор break прекращает выполнение ближайшего внешнего для него оператора цикла. Оператор continue передает управление на ближайшую внешнюю проверку условия продолжения цикла.

Для иллюстрации рассмотрим фрагмент другой программы для вычисления суммы произведений элементов строк той же матрицы:

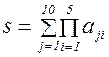
double a[10][5];

for (j=0,s=0.0; j<10; j++)

{

for (i=0,p=1.0; i<5; i++)

{

if (a[j][i] ==0.0) break;

p*=a[j][i];

}

if (i <5) continue;

s+=p;

}

Внутренний цикл по i прерывается, если обнаруживается нулевой элемент матрицы. В этом случае произведение элементов столбца заведомо равно нулю, и его не нужно вычислять. Во внешнем цикле проверяется значение i. Если i<5, т.е. элемент a[j][i] оказался нулевым, то оператор continue передает управление на ближайший оператор цикла, и, таким образом, не происходит увеличение s на величину "недосчитанного" значения р. Если внутренний цикл завершен естественно, то i равно 5, и оператор continue не может выполняться.

Упорядочение в одномерных массивах. Для демонстрации некоторых особенностей вложения циклов и работы с массивами рассмотрим простейшие алгоритмы сортировки. Необходимо, введя значение переменной 1<n<=100 и значения n первых элементов массива а[0],а[1],...,а[n-1], упорядочить эти первые элементы массива по возрастанию их значений. Текст первого варианта программы:

/* Упорядочение элементов массива */

#include <stdio.h>

main( )

{

int n,i,j;

double a[100],b;

while(1)

{

printf("\n Введите количество элементов n=") ;

scanf("%d",&n);

if (n > 1 && n <= 100) break;

printf ("Ошибка! Необходимо 1<n<=100! ") ;

}

printf("\n Введите значения элементов массива:\n");

for(j=0; j<n;j++)

{

printf("a[%d]=”, j+1) ;

scanf(“%lf”,&a[j]);

}

for(i=0; i<n-1; i++)

for(j=i+l; j<n; j++)

if(a[i]>a[j])

{

b=a[i]; a[i]=a[j];. a[j]=b;

}

printf("\n Упорядоченный массив: \n") ;

for(j=0; j<n; j++)

printf("a[%d]=%f\n", j+1,a[j]);

}

При заполнении массива и при печати результатов его упорядочения индексация элементов выполнена от 1 до n, как это обычно принято в математике. В программе на Си это соответствует изменению индекса от 0 до (n-1).

В. программе реализован алгоритм прямого упорядочения - каждый элемент a[i], начиная с а[0] и кончая а[n-2], сравнивается со всеми последующими, и на место a[i] выбирается минимальный. Таким образом, а[0] принимает минимальное значение, а[1] - минимальное из оставшихся и т.д. Недостаток этого алгоритма состоит в том, что в нем фиксированное число сравнений, не зависимое от исходного расположения значений элементов. Даже для уже упорядоченного массива придется выполнить то же самое количество итераций (n-1)*n/2, так как условия окончания циклов не связаны со свойствами, т.е. с размещением элементов массива.

Алгоритм попарного сравнения соседних элементов позволяет в ряде случаев уменьшить количество итераций при упорядочении. В цикле от 0 до n-2 каждый элемент a[i] массива сравнивается с последующим a[i+l] (0<i<n-l). Если a[i]>a[i+l], то значения этих элементов меняются местами. Упорядочение заканчивается, если оказалось, что a[i] не больше a[i+l] для всех i. Пусть k - количество перестановок при очередном просмотре. Тогда упорядочение можно осуществить с помощью такой последовательности операторов:

do {

for (i=0, k=0; i<n-l; i++)

if ( a[i] > a[i+l] )

{

b=a[i]; a[i]=a[i+1]; a[i+1]=b;

k=k+l;

}

n--;

}

while ( k > 0 ) ;

Здесь количество повторений внешнего цикла зависит от исходного расположения значений элементов массива. После первого завершения внутреннего цикла элемент а[n-1] становится максимальным. После второго окончания внутреннего цикла на место а[n-2] выбирается максимальный из оставшихся элементов и т.д. Таким образом, после j-гo выполнения внутреннего цикла элементы a[n-j],...,a[n-l] уже упорядочены, и следующий внутренний цикл достаточно выполнить только для 0<i<(n-j-l). Именно поэтому после каждого окончания внутреннего цикла значение n уменьшается на 1.

В случае упорядоченности исходного массива внешний цикл повторяется только один раз, при этом выполняется (n-1) сравнений, k остается равным 0. Для случая, когда исходный массив упорядочен по убыванию, количество итераций внешнего цикла равно (n-1), а внутренний цикл последовательно выполняется (n-1)*n/2 раз.

Инициализация массивов. Инициализация - это объединение определения объекта с одновременным присваиванием ему конкретного значения. Использование инициализации позволяет изменить формат определения массива. Например, можно явно не указывать количество элементов одномерного массива, а только перечислить их начальные значения в списке инициализации:

double d[ ]={1.0, 2.0, 3.0, 4.0, 5.0};

В данном примере длину массива компилятор вычисляет по количеству начальных значений, перечисленных в фигурных скобках. После такого определения элемент d[0] равен 1.0, d[l] равен 2.0 и т.д. до d[4], который равен 5.0.

Если в определении массива явно указан его размер, то количество начальных значений не может быть больше количества элементов в массиве. Если количество начальных значений меньше, чем объявленная длина массива, то начальные значения получат только первые элементы массива (с меньшими значениями индекса):

int M[8]={8,4,2};

В данном примере определены значения только переменных М[0], М[1] и М[2], равные соответственно 8, 4 и 2. Элементы М[3],..., М[7] не инициализируются.

Правила инициализации многомерных массивов соответствуют определению многомерного массива как одномерного, элементами которого служат массивы, размерность которых на единицу меньше, чем у исходного массива. Одномерный массив инициализируется заключенным в фигурные скобки списком начальных значений. В свою очередь, начальное значение, если оно относится к массиву, также представляет собой заключенный в фигурные скобки список начальных значений. Например, присвоить начальные значения вещественным элементам двумерного массива А, состоящего из трех "строк" и двух "столбцов", можно следующим образом:

double А[3][2]={{10,20}, (30,40), {50,60}};

Эта запись эквивалентна последовательности операторов присваивания: А[0][0]=10; А[0][1]=20; А[1][0]=30; А[1][1]=40; А[2][0]=50; А[2][1]=60;. Тот же результат можно получить с одним списком инициализации:

double A[3][2]={10,20,30,40,50,60};

С помощью инициализаций можно присваивать значения не всем элементам многомерного массива. Например, чтобы инициализировать только элементы первого столбца матрицы, ее можно описать так:

double Z[4][6]={{1}, {2}, (3), {4}};

Следующее описание формирует "треугольную" матрицу в целочисленном массиве из 5 строк и 4 столбцов:

int х[5][4]={{1), {2,3}, {4,5,6}, {7,8,9,10} };

В данном примере последняя пятая строка х[4] остается незаполненной. Первые три строки заполнены не до конца.