Замечания.

1. Выполнение условий (7.1) является необходимым условием дифференцируемости функции 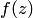в точке. Следовательно, их невыполнения достаточно для утверждения о том, что функция не является дифференцируемой в соответствующей точке.

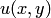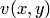2. Условия (7.1) не являются достаточными. Согласно п.2 утверждения 1 в соответствующей точке должны быть дифференцируемы функции и . Напомним, что условием дифференцируемости функции двух действительных переменных в точке является существование и непрерывность частных производных в этой точке.

Из утверждения 1 и замечаний следует правило исследования функции на дифференцируемость.

Правило 1. Для исследования функции на дифференцируемость и нахождения ее производной следует выполнить следующие операции.

1. Для заданной функции 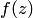найти действительную и мнимую части:

2. Найти частные производные функций .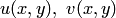

3. Проверить выполнение условий Коши-Римана. Точки, в которых эти условия не выполняются, являются точками, где функция не дифференцируема. Точки, в которых условия (7.1) выполняются и частные производные являются непрерывными, принадлежат области, где функция дифференцируема.

4. Записать выражение производной в точках дифференцируемости по одной из формул (7.2).

Пример 3. Исследовать на дифференцируемость функцию .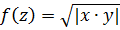

Решение. Рассмотрим два случая.

Первый случай 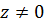. 1. , .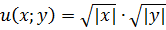

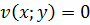2.Очевидно, что 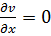, 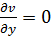в любой точке. Учитывая определение модуля 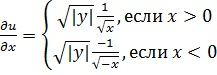, аналогично .

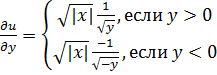3. Проверяем условия (7.1). Условие 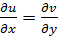выполняется в точках, в которых 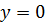при любом 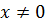. Условие 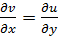выполняется в точках, в которых 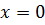при любом 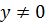. Вместе эти условия не выполняются ни в одной точке. Следовательно, функция не является дифференцируемой.

Второй случай 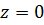. Найдем частные производные функции в точке 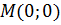используя определение производной 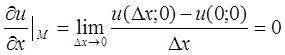, так как u=0 при любом значении аргумента. Аналогично

.

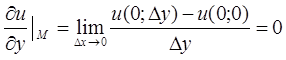Так как 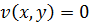, то .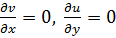

3. Условия Коши-Римана в точке 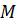выполняются, следовательно, осталось проверить дифференцируемость функции в этой точке. Делаем это по определению производной. Пусть в точке 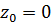получит приращение 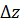, тогда функция получит приращение 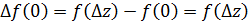. Тогда .

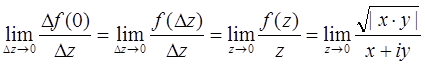Производная существует, если предел не зависит от способа приближения точки 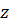к нулю. Пусть приближается по прямой 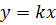или в комплексной форме 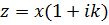. Тогда предел будет иметь вид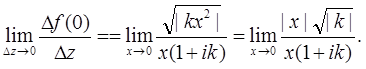

Как видим, при 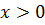предел равен величине 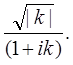т

А при 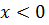величине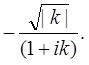

Следовательно, предела не существует, а значит, не существует и производной в точке .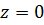

Таким образом, заданная функция не дифференцируема всюду.