В простой замкнутой сети с учетом потерь мощности
Рассмотрим линию с двухсторонним питанием, к которой преобразуется простая замкнутая сеть (рис.3.10,а). Мощности 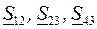 определим сначала без учета потерь по выражениям (3.28), (3.29), (3.26). Предположим, что направления мощностей соответствуют точке потокораздела в узле 3, который отмечен треугольником. «Разрежем» линию в узле 3 (рис.3.10,б) и рассчитаем потоки мощности в линиях 13 и 43!, как это делалось для разомкнутых сетей.
определим сначала без учета потерь по выражениям (3.28), (3.29), (3.26). Предположим, что направления мощностей соответствуют точке потокораздела в узле 3, который отмечен треугольником. «Разрежем» линию в узле 3 (рис.3.10,б) и рассчитаем потоки мощности в линиях 13 и 43!, как это делалось для разомкнутых сетей.
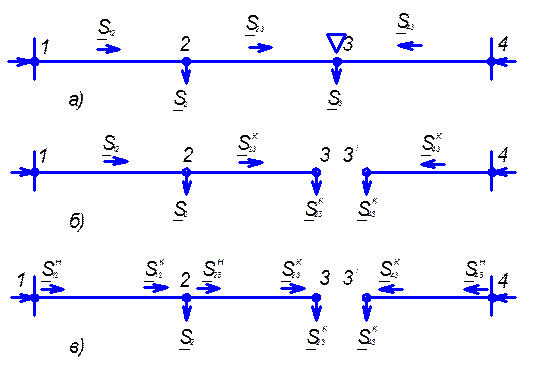
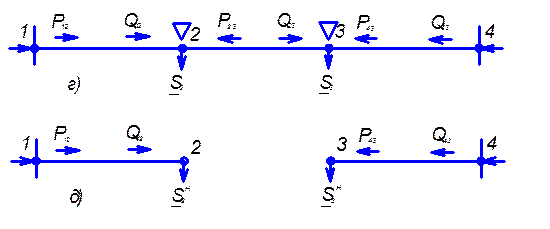
Рис.3.10 Распределение потоков мощности в замкнутой сети
с учетом потерь мощности: а – исходная сеть; б – представление
исходной сети в виде двух линий; в – условные обозначения для
расчета потоков в линиях с учетом потерь мощности; г – направления потоков в случае несовпадения точек потокораздела активной и реактивной мощностей; д – разделение сети при несовпадающих точках потокораздела активной и реактивной мощностей.
На участке 23 потери активной мощности
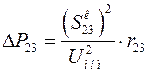 , потери реактивной мощности
, потери реактивной мощности 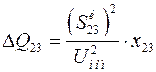 ,
,
потери полной мощности 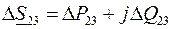 . Находим значение потока мощности
. Находим значение потока мощности 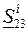 в начале участка 23 (рис.3.10,в):
в начале участка 23 (рис.3.10,в): 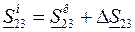 . Далее расчет потоков мощности на участке 12 проводится как для разомкнутых сетей.
. Далее расчет потоков мощности на участке 12 проводится как для разомкнутых сетей.
Может оказаться, что первый этап расчета кольцевой сети выявит две точки потокораздела: одну – для активной, а другую – для реактивной мощности. Такой случай иллюстрируется на рис.3.10,г, где узел 2 – точка потокораздела для активной, а узел 3 – для реактивной мощности. В этом случае кольцевая сеть для дальнейшего расчета может быть также разделена на две разомкнутые линии.
Вычислим предварительно потери мощности на участке между точками потокораздела:
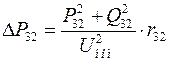 ;
; 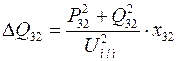 .
.
Если теперь принять, что в точке 2 включена нагрузка
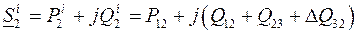 , а в точке 3 – нагрузка
, а в точке 3 – нагрузка 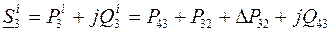 ,
,
где 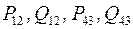 определяются по (3.28), (3.29), а
определяются по (3.28), (3.29), а 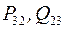 - по (3.26), то при дальнейшем расчете можно вместо кольцевой схемы рассматривать две разомкнутые линии, показанные на рис.3.10,д.
- по (3.26), то при дальнейшем расчете можно вместо кольцевой схемы рассматривать две разомкнутые линии, показанные на рис.3.10,д.
Дата добавления: 2015-10-09; просмотров: 1437;
